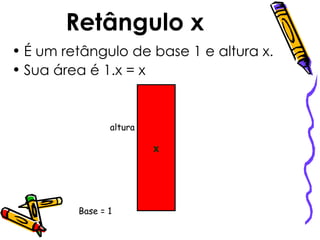
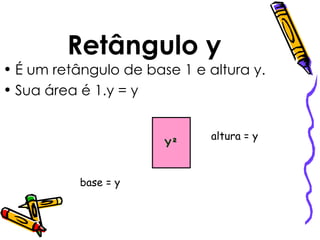
1) O documento apresenta diferentes formas geométricas (retângulos, quadrados) e suas áreas, representadas por monômios. 2) Exemplos mostram como representar operações algébricas (adição, subtração, multiplicação) com essas formas geométricas. 3) A multiplicação de monômios é explicada como a construção de um retângulo cuja área é dada pelo produto dos coeficientes e das partes literais, observando a regra de somar expoentes.

1. ALGEPLAN Uma maneira interessante de estudar operações e produtos notáveis Profª Regina Carla de Azevedo

2. Conhecendo as peças

3. Quadrado x² É um quadrado de base x e altura x. Sua área é x . x = x² altura: x Base = x x²

4. Quadrado y² É um quadrado da base y e altura y. Sua área é y.y = y² altura = y base = y y²

5. Quadrado 1 É um quadrado de base 1 e altura 1. Sua área é 1.1 = 1 altura = 1 base = 1 1

6. Retângulo xy É um retângulo de base y e altura x. Sua área é x.y = xy altura= x base = y xy

7. Retângulo x É um retângulo de base 1 e altura x. Sua área é 1.x = x altura = x Base = 1 x

8. Retângulo y É um retângulo de base 1 e altura y. Sua área é 1.y = y altura = y base = y Y²

9. Adição e subtração: x² + 2xy – 3x + x² - xy + x Representado com as peças x² xy -x -xy x x² xy -x -x Resultado: 2x²+ xy - 2x

10. Conclusão: Representamos a operação com as figuras. Agrupamos os termos semelhantes (mesma forma). Somamos ou subtraímos os termos semelhantes. Escrevemos o resultado ordenando os monômios observando a ordem decrescente dos expoentes.

11. Outro exemplo: (2xy + x + 3)-(3xy – x + 1) Primeiro devemos eliminar os parêntesis lembrando que o sinal de – antes de um ( ) significa o oposto do polinômio. Assim fica: 2xy + x + 3 – 3xy + x -1 x x xy xy 1 1 1 -xy -xy -xy -1 Resultado : 2x – xy + 2

12. Multiplicação de monômios Construa o retângulo de base 3x e altura 2x. Qual é a área desse retângulo? É base x altura Ou seja: 3x . 2x = 6x² ,isto quer dizer que no interior desse retângulo cabem 6 quadrados x² Veja a comprovação olhando a figura. x x x x x x x x x x x² x² x² x² x² x² x²

13. Outro exemplo Construa um retângulo de base 3x e altura 4. Qual é a área desse retângulo? É base x altura, ou seja: 3x . 4 = 12x, isto que dizer que no interior desse retângulo cabem 12 retângulos x. Observe a comprovação pelas figuras x x x 1 1 1 1 x x x 1 1 1 1 x x x x x x x x x x x x

14. Qual a base e altura de um retângulo de área 4xy? Vamos partir do contrário, ou seja, representar o interior para sabermos a medida da base e da altura. Comparando com as formas concluímos que a base é 4y e altura x. xy xy xy xy x y y y y

15. Construa um quadrado de área 4y². Vamos usar 4 peças y² e formar um quadrado. Qual o valor da base e da altura desse quadrado? Comparando com as peças concluímos que a base é 2y e a altura também é 2y. y² y² y² y² y y y y

16. Conclusão: Multiplicamos os coeficientes dos monômios. Multiplicamos a parte literal, lembrando que: na multiplicação de potências de mesma base, conservamos a base e somamos os expoentes