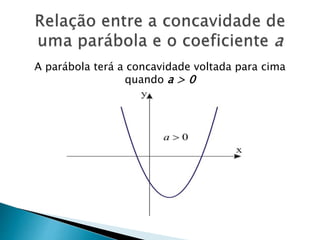
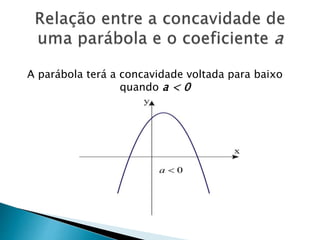
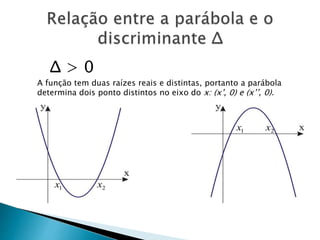
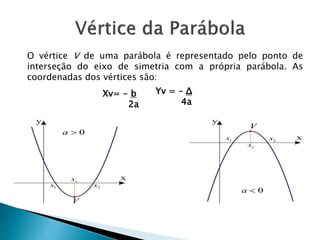
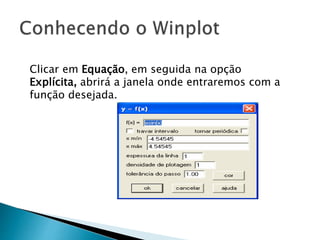
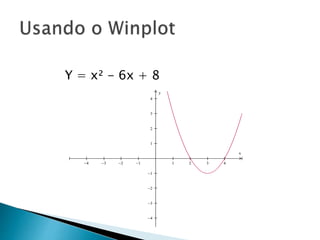
O documento discute funções polinomiais do segundo grau, também chamadas de funções quadráticas. Apresenta exemplos de funções quadráticas e explica que seu gráfico é uma parábola. Detalha como calcular as raízes e o vértice da parábola e como esboçar seu gráfico usando o software Winplot.

1. Projeto Final
Por Meireluce Assis Duarte

2. Felizes aqueles que se divertem com
problemas que educam a alma e
elevam o espírito. (Fénelon)

3. Funções Polinomiais do 2º Grau

4. Chama-se Função Polinomial do 2º grau ou
Função Quadrática qualquer função f de R em
R dada por uma lei da forma f(x) = ax² + bx
+ c, com a, b e c números reais e a ≠ 0.

5. Exemplos:
 f(x) = 2x² + 5x + 6, onde a = 2, b = 5 e c = 6.
 f(x) = -x² + x - 1, onde a = -1, b = 1 e c = -1.
 f(x) = 3/2x² + 1/3, onde a = 3/2, b = 0 e c = 1/3.

6. Em um sistema ortogonal, o gráfico de uma
função quadrática é representado por uma
curva, a qual damos o nome de parábola.

7. A parábola terá a concavidade voltada para cima
quando a > 0

8. A parábola terá a concavidade voltada para baixo
quando a < 0

9. A função tem duas raízes reais e distintas, portanto a parábola
determina dois ponto distintos no eixo do x: (x’, 0) e (x’’, 0).
Δ > 0

10. Δ = 0
A função tem duas raízes reais e iguais: x’ = x’’,
portanto a parábola tangencia o eixo do x

11. Δ < 0
A função não tem duas raízes reais: x’ = x’’, portanto a
parábola não determina nenhum ponto no eixo do x.

12. O vértice V de uma parábola é representado pelo ponto de
interseção do eixo de simetria com a própria parábola. As
coordenadas dos vértices são:
Yv = – Δ
4a
Xv= - b
2a

13. Esboce o gráfico cartesiano para cada função
quadrática. Siga o esquema abaixo:
 Determine as raízes;
 Determine as coordenadas do vértice;
 Monte uma tabela para os valores de x e y;
 Esboce o gráfico utilizando papel
quadriculado.

14. a) Y = x² - 6x + 8
b) Y = x² - 6x + 9
c) Y = -x² - 2x + 3
d) Y = x² - x + 1
e) Y = -2x² + 7x - 3

15. O Winplot foi desenvolvido pelo professor
Richard Parris, da Philips Exeter Academy
(EUA), por volta de 1985. Escrito em
linguagem C, chamava-se PLOT e rodava no
antigo DOS.

16. O programa foi rebatizado quando foi
lançado o Windows 3.1. A versão para
Windows 98 surgiu em 2001 e está escrita
em linguagem C++.

17. Além do português (traduzido por Adelmo
Ribeiro de Jesus, professor Bahiano), o
software está disponível em mais 13 idiomas.

18.  O Winplot é um bom plotador de gráficos e,
apesar de não possuir uma interface gráfica
tão sofisticada como outros softwares, como
GeoGebra e Maple, possibilita um manuseio
fácil e rápido. Além disso, é um programa
“leve” e funciona em praticamente qualquer
computador.

19. Ao abrir o programa, a janela mostrada na
figura deverá aparecer, ao clicar em janela
aparecerá as opções de gráficos 2-dim (duas
dimensões) ou 3-dim (três dimensões).

20. Para as funções quadráticas, usaremos os
gráficos em duas dimensões.

21. Clicar em Equação, em seguida na opção
Explícita, abrirá a janela onde entraremos com a
função desejada.

22. Construir os gráficos da funções dadas em
Atividades Preliminares.

23.        








x
y
Y = x² - 6x + 8

24.  Atividades desenvolvidas com turmas de
concluintes do 9º ano do Ensino Fundamental, ou
seja, 1º ano do Ensino Médio.
 Atividades desenvolvidas em 4 aulas, com
exposição do conteúdo (Revisão) pela professora
regente.
 Atividades do laboratório de informática
realizadas em grupos de 4 (quatro) alunos,
devido à quantidade reduzida de computadores.
 Participação e interesse de todos, com objetivos
atingidos.

25.  BARRETO FILHO, Benigno, 1952-
Matemática aula por aula: volume único: ensino
médio/Benigno Barreto Filho, Cláudio Xavier Barreto. –
São Paulo: FTD, 2000.
 BONJORNO, José Roberto
Matemática: Fazendo a diferença/José Roberto
Bonjorno, Regina Azenha Bonjorno, Ayrton Olivares. –
1.ed. – São Paulo: FTD, 2006 – Coleção Fazendo a
Diferença.
 http://w3.ufsm.br/petmatematica/arquivos/Apostila%2
0Winplot.pdf. Acesso em 04/03/2015.
 http://www.pucrs.br/famat/fmoreira/economiaII/WINPL
OT.pdf. Acesso em 04/03/2015.