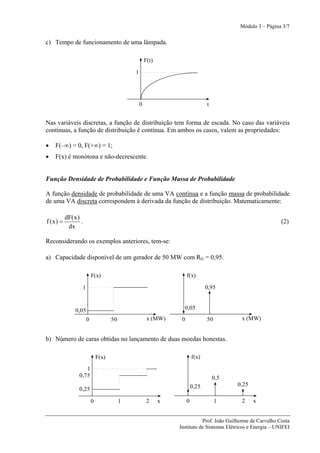
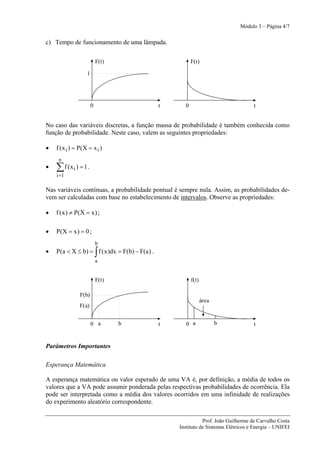
O documento apresenta conceitos básicos sobre variáveis aleatórias, incluindo sua definição, classificação, funções de distribuição e densidade de probabilidade. Exemplos ilustram como modelar variáveis aleatórias em problemas de geração de energia elétrica, e são apresentados parâmetros como esperança matemática e variância para caracterizar as variáveis. Problemas propostos aplicam os conceitos ao cálculo da capacidade estática de sistemas de geração.

1. Módulo 3 – Página 1/7
MÓDULO 3
VARIÁVEIS ALEATÓRIAS
3.1 – Variável Aleatória
Uma variável aleatória (VA) é uma função que faz corresponder a cada elemento de um espa-
ço de possibilidades, um valor numérico de interesse para o experimento em questão.
e1 e2 ei S X
...
en
...
R
X(ei) = xi
Na figura acima, X é uma variável aleatória e X(ei) = xi é um resultado numérico associado ao
evento ei, que representa uma característica quantificável do mesmo.
Exemplos
a) Um gerador com capacidade de 50 MW pode ser encontrado em 2 estados: disponível e
avariado. O espaço de possibilidades é S = {disponível, avariado}.
Pode-se definir a VA: X = “Capacidade disponível do gerador”. Assim:
⎧50, se e = disponível
X (e ) = ⎨
⎩0, se e = avariado.
b) Ao lançar duas moedas e observar a face de cima, tem-se S = {(cara, cara), (cara, coroa),
(coroa, cara), (coroa, coroa)}.
Seja X = “Número de caras obtidas no lançamento de duas moedas”. Logo:
⎧2, se e = (cara, cara)
⎪
X(e) = ⎨1, se e = (cara, coroa) ou (coroa, cara)
⎪0, se e = (coroa, coroa).
⎩
c) Ao contar o número de peças defeituosas em um lote de 10 produzidas por uma fábrica,
tem-se S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Se X = “Número de peças defeituosas em um total de 10”, então:
X(e) = e.
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

2. Módulo 3 – Página 2/7
Observe que neste caso, os elementos do espaço de possibilidades já são numéricos e re-
presentam a própria característica que se deseja avaliar.
d) Ao se observar o tempo de funcionamento de uma lâmpada até que esta se queime, tem-se
S = {t | t ≥ 0}. Pode-se definir a VA: T = “Tempo de funcionamento até à falha”.
T(t) = t.
3.2 – Caracterização de uma Variável Aleatória
As variáveis aleatórias podem ser:
• Discretas: Admitem um número finito ou uma quantidade enumerável de valores. Exem-
plos: (a), (b) e (c) anteriores.
• Contínuas: Podem assumir infinitos valores. Normalmente são resultantes de processos de
medição. Exemplo: (d) anterior.
Função de Distribuição
A função de distribuição de uma VA fornece para todo valor –∞ < x < +∞, a probabilidade de
a VA assumir valores menores ou iguais a x. Assim:
F(x) = P(X ≤ x). (1)
Reconsiderando os exemplos anteriores:
a) Capacidade disponível de um gerador de 50 MW com RG = 0,95.
F(x)
1
0,05
0 50 x (MW)
b) Número de caras obtidas no lançamento de duas moedas honestas.
F(x)
1
0,75
0,25
0 1 2 x
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

3. Módulo 3 – Página 3/7
c) Tempo de funcionamento de uma lâmpada.
F(t)
1
0 t
Nas variáveis discretas, a função de distribuição tem forma de escada. No caso das variáveis
contínuas, a função de distribuição é contínua. Em ambos os casos, valem as propriedades:
• F(–∞) = 0, F(+∞) = 1;
• F(x) é monótona e não-decrescente.
Função Densidade de Probabilidade e Função Massa de Probabilidade
A função densidade de probabilidade de uma VA contínua e a função massa de probabilidade
de uma VA discreta correspondem à derivada da função de distribuição. Matematicamente:
dF( x )
f (x) = . (2)
dx
Reconsiderando os exemplos anteriores, tem-se:
a) Capacidade disponível de um gerador de 50 MW com RG = 0,95.
F(x) f(x)
1 0,95
0,05 0,05
0 50 x (MW) 0 50 x (MW)
b) Número de caras obtidas no lançamento de duas moedas honestas.
F(x) f(x)
1
0,75 0,5
0,25 0,25
0,25
0 1 2 x 0 1 2 x
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

4. Módulo 3 – Página 4/7
c) Tempo de funcionamento de uma lâmpada.
F(t) F(t)
1
0 t 0 t
No caso das variáveis discretas, a função massa de probabilidade é também conhecida como
função de probabilidade. Neste caso, valem as seguintes propriedades:
• f ( x i ) = P(X = x i )
n
• ∑ f (x i ) = 1 .
i =1
Nas variáveis contínuas, a probabilidade pontual é sempre nula. Assim, as probabilidades de-
vem ser calculadas com base no estabelecimento de intervalos. Observe as propriedades:
• f ( x ) ≠ P( X = x ) ;
• P(X = x ) = 0 ;
b
• ∫
P(a < X ≤ b) = f ( x )dx = F(b) − F(a ) .
a
F(t) f(t)
F(b)
área
F(a)
0 a b t 0 a b t
Parâmetros Importantes
Esperança Matemática
A esperança matemática ou valor esperado de uma VA é, por definição, a média de todos os
valores que a VA pode assumir ponderada pelas respectivas probabilidades de ocorrência. Ela
pode ser interpretada como a média dos valores ocorridos em uma infinidade de realizações
do experimento aleatório correspondente.
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

5. Módulo 3 – Página 5/7
n
• Para uma VA discreta: E(X) = μ = ∑ x i P( x i ) . (3)
i =1
+∞
• Para uma VA contínua: E(X) = μ = ∫ x f (x) dx . (4)
−∞
A esperança matemática é uma medida de tendência central, i.e. indica o ponto em torno do
qual a VA tende a se distribuir.
Variância e Desvio-Padrão
A variância e o desvio-padrão são medidas de dispersão. A variância corresponde à média dos
quadrados das distâncias entre todos os valores da VA e seu centro (esperança matemática):
V(X) = E[(X − μ) 2 ] = E(X 2 ) − [E(X)]2 . (5)
Em uma VA discreta, tem-se:
n
V ( X ) = σ 2 = ∑ ( x i − μ ) 2 P( x i ) . (6)
i =1
Para uma VA contínua:
+∞
V(X) = σ 2 = ∫ ( x − μ)
2
f ( x ) dx . (7)
−∞
O desvio-padrão corresponde à raiz quadrada da variância e é mais utilizado por ter a mesma
dimensão da grandeza representada pela VA. Por exemplo, se a VA for expressa em MW, a
variância será dada em MW2 e o desvio-padrão em MW.
σ = V(X) . (8)
3.3 – Exercícios Propostos
1) Uma caixa contém 3 bolas brancas e uma bola preta. Uma pessoa vai retirar as bolas uma
por uma, até conseguir apanhar a bola preta. Seja X o número de tentativas que serão ne-
cessárias. Determine a função densidade de probabilidade, a função de distribuição, a mé-
dia e a variância de X.
2) Uma moeda honesta é lançada sucessivamente até sair cara ou até serem feitos 3 lança-
mentos. Considere a variável aleatória “número de lançamentos realizados”. Construa o
gráfico de sua função de distribuição e calcule sua média e variância.
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

6. Módulo 3 – Página 6/7
3.4 – Aplicações ao Cálculo da Capacidade Estática de Sistemas de Geração
1 – Aplicação Inicial (Conceitos Básicos de Probabilidades e Variáveis Aleatórias)
Um sistema de geração é constituído por 4 geradores iguais com capacidade nominal de 100
MW e indisponibilidade de 0,04. O pico de carga do sistema vale 270 MW. Pede-se:
a) Organizar numa tabela, o espaço de possibilidades (completo) do experimento “observar o
estado dos quatro geradores”. Note que existirão 16 estados!
b) Calcule a probabilidade do sistema não atender à carga.
c) Calcule a probabilidade de um (e somente um) gerador qualquer ser encontrado avariado.
d) Qual a probabilidade de se encontrar o gerador 2 avariado?
e) Dado que o gerador 1 está avariado, qual a probabilidade do gerador 3 estar avariado?
f) Dado que um (e só um) gerador está avariado, qual a probabilidade de ser o gerador 1?
g) Calcule em uma tabela e esboce em um gráfico, a função densidade de probabilidade e a
função de distribuição da capacidade de geração disponível.
h) Calcule a esperança matemática do número de geradores disponíveis no sistema.
i) Calcule a esperança matemática da capacidade de geração disponível no sistema.
j) Calcule o valor médio do corte de carga do sistema.
k) Calcule o valor médio do corte de carga, sabendo que o mesmo é maior que zero.
2 – Tabela de Capacidades Disponíveis
A tabela de capacidades disponíveis reúne todas as possíveis capacidades de geração que um
sistema pode apresentar associadas às respectivas probabilidades. Para detalhamentos sobre a
montagem de tabelas de capacidades, consulte as referências bibliográficas.
Considere o sistema abaixo e determine sua tabela de capacidades.
- 4 unidades de 25 MW com indisponibilidade 0,10;
- 2 unidades de 50 MW com indisponibilidade 0,02;
3 – Índices de Perda de Carga e Energia
Os seguintes índices são usados para quantificar o desempenho de um sistema de geração:
• LOLP – Loss of Load Probability
Representa a probabilidade da carga ultrapassar a capacidade de geração disponível.
• LOLE – Loss of Load Expectation
Corresponde ao número médio de horas num determinado período (geralmente 1 ano) em
que se espera que a carga seja maior que a geração. Pode ser calculada como,
LOLE = LOLP × 8760 (horas/ano).
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI

7. Módulo 3 – Página 7/7
• EPNS – Expected Power Not Supplied
É o valor médio da potência não suprida em MW, i.e. corresponde à esperança matemática
do corte de carga.
• EENS – Expected Energy Not Supplied
É o valor esperado da energia não suprida pelo sistema em um determinado período (em
geral, 1 ano) em MWh. Matematicamente,
EENS = EPNS × 8760 (MWh/ano).
Calcule os índices de confiabilidade do sistema da Aplicação 2 (Tabela de Capacidades Dis-
poníveis), considerando que este deve suprir uma carga de 85 MW.
4 – Consideração de Incertezas na Previsão de Carga
As aplicações anteriores assumiram que a carga do sistema é conhecida com exatidão. No
entanto, os estudos de confiabilidade aplicados ao planejamento da expansão dos sistemas são
feitos considerando um horizonte de anos à frente. Assim, existirá sempre uma incerteza asso-
ciada à previsão da carga, o que impede a determinação exata dos índices de confiabilidade.
Para avaliar este problema, calcule a probabilidade do sistema da Aplicação 2 não atender à
carga descrita na figura abaixo. Note que estão representados os possíveis valores que a carga
pode assumir e as respectivas probabilidades de ocorrência.
0,60
0,20 0,20
65 85 105 Carga (MW)
3.5 – Trabalho Proposto: Desenvolvimento de Programa Computacional
a) Desenvolva um algoritmo capaz de fornecer a tabela de capacidades de um sistema de
geração constituído por geradores com capacidades e indisponibilidades diferentes. A ta-
bela deve listar os possíveis valores de capacidade e probabilidades.
b) Inclua no programa, o cálculo dos índices de confiabilidade apresentados anteriormente.
c) Executar o programa para calcular os índices LOLP, LOLE, EPNS e EENS do sistema de
geração com carga-pico de 220 MW, composto pelas quatro usinas geradoras abaixo:
Usina 1: 2 unidades de 20 MW com indisponibilidade 0,08;
Usina 2: 3 unidades de 50 MW com indisponibilidade 0,04;
Usina 3: 2 unidades de 30 MW com indisponibilidade 0,06;
Usina 4: 1 unidade de 100 MW com indisponibilidade 0,02.
Prof. João Guilherme de Carvalho Costa
Instituto de Sistemas Elétricos e Energia – UNIFEI