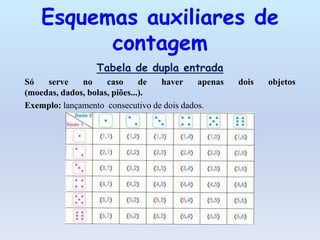
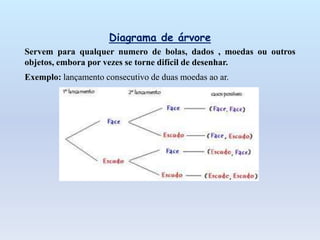
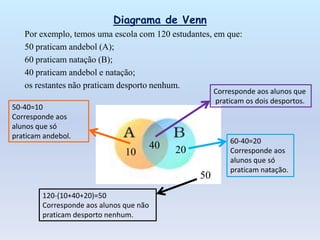
O documento discute os conceitos básicos de probabilidade, incluindo experiências aleatórias versus deterministas, espaço amostral, tipos de eventos, a lei de Laplace para calcular probabilidades e alguns esquemas auxiliares para contagem como tabelas de dupla entrada e diagramas de árvore e Venn.

2. O que são probabilidades?
• Existem dois tipos de experiências:
Aleatórias Deterministas
Quando, à partida, não sabemos o Quando, à partida, já conhecemos
resultado. o resultado.
Exemplos: Lançamento de uma Exemplos: furar um balão
moeda, totoloto, extração de uma cheio, deixar cair um prego num
carta, etc.. copo de água, etc..
• Uma probabilidade é uma forma de medir as hipóteses que um dado
acontecimento tem de ocorrer.
 As probabilidades interessam-se pelas experiências aleatórias!

3. Espaço de resultados
• O espaço de resultados ou espaço amostral é o conjunto de todos os
resultados possíveis de uma experiência aleatória.
Representa-se por E, S ou Ω.
• Exemplo: Lançamento de um dado
Espaço amostral = E= {1,2,3,4,5,6}

4. Acontecimentos
• Um acontecimento é um subconjunto do espaço amostral.
• Um acontecimento identifica-se como o conjunto dos seus casos
favoráveis.
Tipos de Acontecimentos
Elementares: quando só tem um elemento.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
A: “sair número 3”
A={3}
Compostos: quando tem mais que um elemento.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
B: “sair número ímpar”
B={1,3,5}

5. Tipos de acontecimentos
Equiprováveis/Igualmente prováveis: têm a mesma probabilidade
de acontecer.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
C: “sair número par”
D: “sair número ímpar”
C e D são equiprováveis!
Certos: verificam-se sempre.
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
E: “sair número inteiro positivo inferior a 7”
E= {1,2,3,4,5,6}
Impossíveis: nunca se verificam.
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
F: “Sair número inteiro positivo superior a 7”
F= {}

6. Lei de Laplace
• A probabilidade de realização de um acontecimento A é igual ao
quociente entre o número de casos favoráveis à sua realização e o
numero total de casos possíveis.
Simon
Laplace
Nasceu em Beaumont-en-Auge, a 23 de
março de 1749 e morreu em Paris, a 5 de
março de 1827. Foi um matemático,
astrónomo e físico francês que, entre outras criações,
fundou a Lei de Laplace.

7. Algumas propriedades que deves
ter em conta no estudo das probabilidades
• Propriedade 1: A probabilidade de um acontecimento impossível
é 0 ou 0%.
• Propriedade 2: A probabilidade de um acontecimento certo é 1
ou 100%.
• Propriedade 3: Em qualquer experiência, a probabilidade de um
acontecimento A é um número maior ou igual a 0 mas menor ou
igual a 1, ou seja:
 Se A é um acontecimento impossível, mas não certo: 0 P(A) 1.
• Propriedade 4: Quando dois acontecimentos A e B não podem
ocorrer ao mesmo tempo: P(A ou B) = P(A) + P(B).

8. Lei dos Grandes Números
• Para um grande número de experiências, a frequência relativa de um
acontecimento A é um valor aproximado da sua probabilidade.
• Assim:
P(A) ≈ Frequência relativa de A
• Sendo assim, podemos supor que, por exemplo:
- se lançarmos uma moeda ao ar 500 vezes e em 400 dessas vezes obtermos
face nacional, podemos considerar que a moeda esteja viciada.

9. Esquemas auxiliares de
contagem
Tabela de dupla entrada
Só serve no caso de haver apenas dois objetos
(moedas, dados, bolas, piões...).
Exemplo: lançamento consecutivo de dois dados.

10. Diagrama de árvore
Servem para qualquer numero de bolas, dados , moedas ou outros
objetos, embora por vezes se torne difícil de desenhar.
Exemplo: lançamento consecutivo de duas moedas ao ar.

11. Diagrama de Venn
Por exemplo, temos uma escola com 120 estudantes, em que:
50 praticam andebol (A);
60 praticam natação (B);
40 praticam andebol e natação;
os restantes não praticam desporto nenhum.
Corresponde aos alunos que
praticam os dois desportos.
50-40=10
Corresponde aos
alunos que só
praticam andebol.
60-40=20
40 20 Corresponde aos
10
alunos que só
praticam natação.
50
120-(10+40+20)=50
Corresponde aos alunos que não
praticam desporto nenhum.