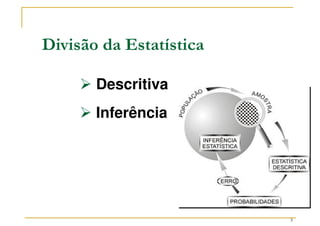
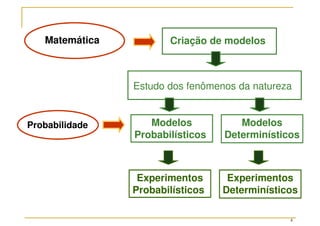
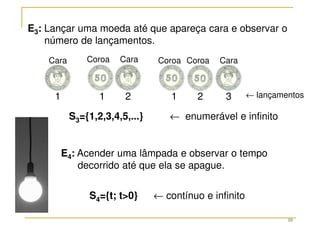
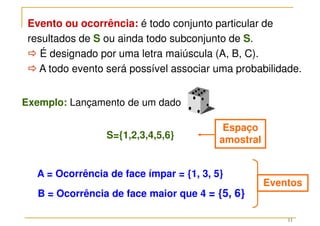
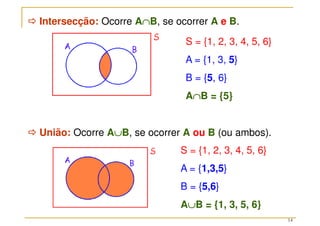
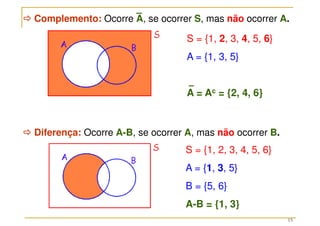
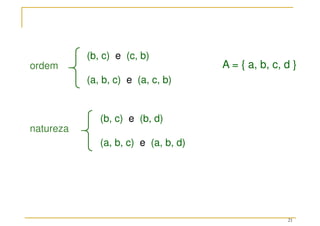
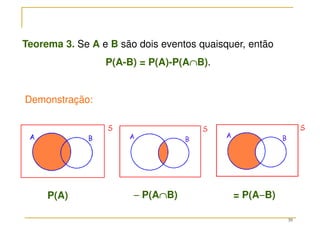
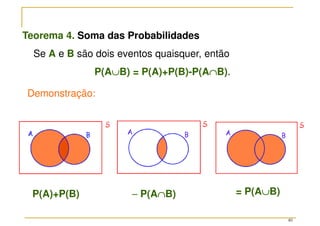
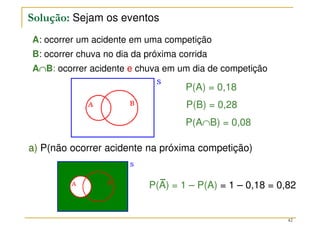
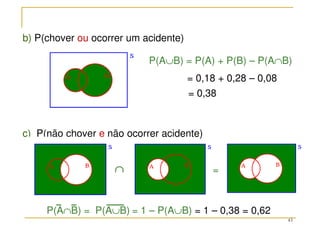
O documento discute conceitos fundamentais da teoria das probabilidades, incluindo definições de probabilidade, experimentos aleatórios e determinísticos, e as operações em eventos. Aborda também técnicas de contagem, a axiomatização de Kolmogorov e a introdução aos conceitos de probabilidade clássica e frequência relativa. Utiliza exemplos práticos para ilustrar os conceitos e métodos de cálculo de probabilidades.