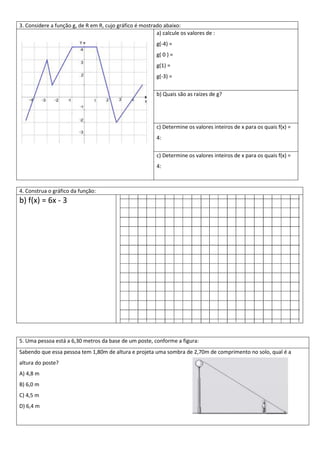
1) O documento contém uma prova suplementar de matemática do 9o ano com 10 questões sobre funções do 1o e 2o grau, trigonometria e equações. 2) A primeira questão pede para representar graficamente uma relação entre dois conjuntos e determinar se é uma função, além de calcular domínio, contradomínio e conjunto imagem. 3) A segunda questão fornece uma função do 1o grau e pede para calcular os coeficientes, a lei de formação e valores de entrada e saída.

1. PROVA SUPLEMENTAR DE MATEMÁTICA – 9º ANO
Aluno:____________________________________________________________ Nº: _______
DATA: 09/12/2011 VALOR: 3,0 PONTOS NOTA: __________
Prof. Adriano Capilupe
Faça a prova com muita calma e atenção, resolva a lápis e só passe a resposta a caneta quando tiver certeza do
resultado. BOA SORTE!
1. Dados os conjuntos A = {-3,-2, -1, 0, 1, 2, 3} e B = {-3, - 2, -1, 0, 1, 2, 3, 4, 5, 6 }, e seja uma relação
dada pela lei de formação:
Determine o que se pede:
a) Faça um diagrama de flechas que representa essa b) Essa relação representa função?
relação.
c) Determine o Domínio dessa relação:
d) Determine o Contradomínio:
e) Determine o Conjunto Imagem
2. A função do 1º grau é dada por y = ax + b sendo que f(0)=3 e f(1)=2. Determine o que se pede:
a) os coeficientes a e b dessa função:
b) A lei de formação dessa função:
c) Calcule
f(-4) e f(5)
d) os valores de x para os quais f(x) = -2

2. 3. Considere a função g, de R em R, cujo gráfico é mostrado abaixo:
a) calcule os valores de :
g(-4) =
g( 0 ) =
g(1) =
g(-3) =
b) Quais são as raízes de g?
c) Determine os valores inteiros de x para os quais f(x) =
4:
c) Determine os valores inteiros de x para os quais f(x) =
4:
4. Construa o gráfico da função:
b) f(x) = 6x - 3
5. Uma pessoa está a 6,30 metros da base de um poste, conforme a figura:
Sabendo que essa pessoa tem 1,80m de altura e projeta uma sombra de 2,70m de comprimento no solo, qual é a
altura do poste?
A) 4,8 m
B) 6,0 m
C) 4,5 m
D) 6,4 m

3. 6. Determine as medidas b e h indicadas no triângulo:
7. Caio está distante 40m da base de um obelisco de 30,4m de altura. Os olhos de Caio estão a x metros do plano
horizontal. Calcule o valor de x (Use: sen 36° = 0,58 cos 36° = 0,80 tg 36° = 0,72)
 1
8. No triangulo DEF, o cos D . Determine o valor de x
5
9. Resolva as equações a seguir:
a) (x + 2)² + x = 0 b) 3x² - 2x -8 = -2x + 67

4. x2 4 d) 9x² + 2x +1 = 0
c) x 2
5
10. Observe, na figura, o gráfico da função quadrática g(x)= ax² + bx + c. Determine o que é pedido em cada
item:
a) As raízes reais de g.
b) O sinal do coeficiente a.
c) O sinal do discriminante delta.
d) As coordenadas de seu vértice V.
e) O valor de g(-2)