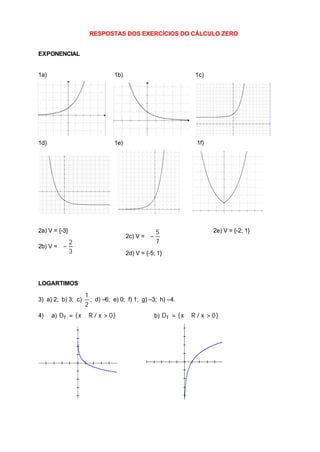
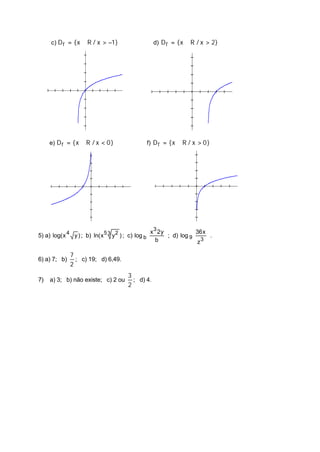
O documento apresenta 7 exercícios sobre exponenciais e logaritmos. Os exercícios incluem esboçar gráficos de funções exponenciais, resolver equações exponenciais, calcular valores de logaritmos, determinar domínios de funções logarítmicas e reduzir expressões com logaritmos. As respostas fornecem os valores ou gráficos solicitados para cada questão.

1. EXERCÍCIOS SOBRE EXPONENCIAL E LOGARITMO
1) Esboce o gráfico das seguintes funções:
a) f(x) = 2x x
x
1 
d) f(x) =   - 3
1  2
b) f(x) =  
2 e) f(x) = 3.2x
c) f(x) = 2x + 2 x
f) f(x) = 2
2) Resolva as seguintes equações exponenciais:
x d) (2x )x + 4 = 32
1 
a)   = 125 e) 4x + 1 – 9.2x + 2 = 0
5 
b) 125x = 0,04
2x + 3
 1 
c) 5 3x-1
= 
 25 
3) Calcule o valor do logaritmo dado.
1
a) log 8 64 b) log 4 64 c) log 64 8 d) log 2
64
e) log 2 1 f) log 2 2 g) log 1 8 h) log 1 81
2 3
4) Determine o domínio e faça um esboço do gráfico da função dada.
a) f (x ) = log 1 x b) f (x ) = log 2 x c) f (x ) = ln( x + 1)
4
d) f (x ) = ln( x − 2) e) f (x ) = log 1 (− x ) f) f (x ) = − log 1 x
2 3
5) Reduza a expressão dada em um único logaritmo.
1 2
a) 4 log x + log y b) 5 ln x + ln y − 3 log 6 1
2 3
c) 3 log b ( x ) + log b (2y ) − 1 d) log 9 x + log 3 6 − 3 log 9 z
3
6) Sendo ln a = 2, ln b = 5, ln = −0,51 , calcule.
5
3b 2
a) ln(ab ) b) ln ab c) ln(a 2 b3 ) d) ln( )
3
5 a
7) Resolva as seguintes equações:
a) ln x + ln 3 = ln 9 c) ln x − ln( x − 1) = ln 2 + ln( 3 − x )
b) ln (x − 2x 2 ) + ln 4 = 0 d) ln x 2 − ln x − ln 4 = 0

2. RESPOSTAS DOS EXERCÍCIOS DO CÁLCULO ZERO
EXPONENCIAL
1a) 1b) 1c)
1d) 1e) 1f)
2a) V = {-3}  5 2e) V = {-2; 1}
2c) V = − 
 2  7
2b) V = − 
 3 2d) V = {-5; 1}
LOGARTIMOS
1
3) a) 2; b) 3; c) ; d) –6; e) 0; f) 1; g) –3; h) –4.
2
4) a) D f = {x ∈ R / x > 0} b) D f = {x ∈ R / x > 0}

3. c) D f = {x ∈ R / x > −1} d) D f = {x ∈ R / x > 2}
e) D f = {x ∈ R / x < 0} f) D f = {x ∈ R / x > 0}
 x3 2y 
5) a) log( x 4 y ) ; b) ln( x 5 3 y 2 ) ; c) log b   ; d) log  36 x  .
 b  9 3 
 
   z 
7
6) a) 7; b) ; c) 19; d) 6,49.
2
3
7) a) 3; b) não existe; c) 2 ou ; d) 4.
2