1) O documento apresenta os conceitos fundamentais de funções matemáticas, incluindo relações binárias, produto cartesiano, domínio, contradomínio e conjunto imagem.
2) São definidas formalmente as noções de função e suas características principais, como cada elemento do domínio ter exatamente uma imagem no contradomínio.
3) São apresentados exemplos de funções constantes, do primeiro e segundo grau, assim como inequações do primeiro e segundo grau. O documento também aborda funções compostas, injetoras,








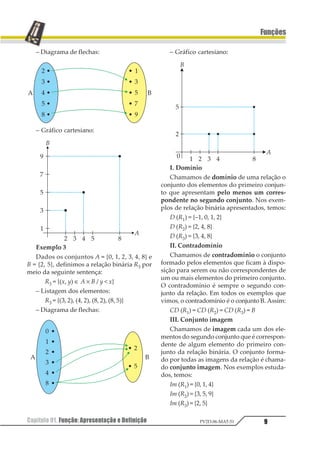

![Capítulo 01. Função: Apresentação e Definição14
Funções
PV2D-06-MAT-51
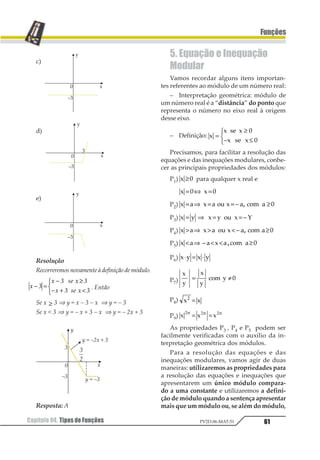
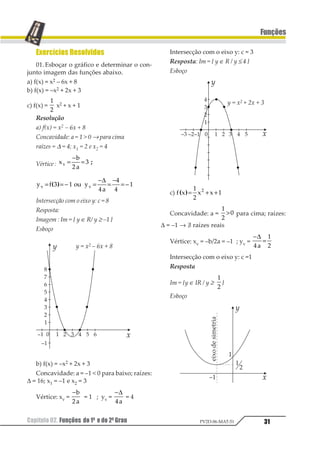
05. (UFRN) Se n(A) = 3 e n(B) = 2, então
(n(A × B))n(A ∩ B) é, no máximo, igual a:
a) 1 d) 18
b) 6 e) 36
c) 12
Resolução
n(A × B) = n(A) n(B) = 3 · 2 = 6
O número máximo de elementos de A ∩ B = 2.
Então, o máximo de (n (A × B)) n(A ∩ B) é 62 = 36
Resposta: E
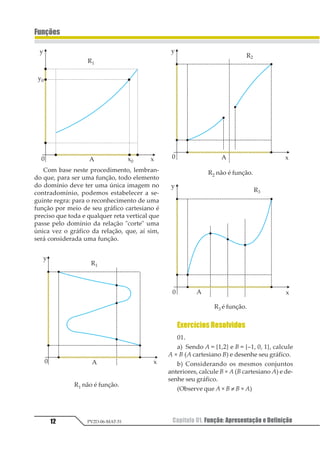
06. (UFU-MG) Quais dos seguintes dia-
gramas definem uma função de X = (a, b, c, d)
em Y = (x, y, z, w)?
a) II, III e IV
b) IV e V
c) I, II e V
d) I e IV
e) I, IV e V.
Resolução
I é função; II não é função, pois d tem 2 corres-
pondentes em Y; III não é função, pois a não tem
correspondente em Y; IV é função; V não é função,
pois a e c têm 2 correspondentes em Y e d não tem
correspondenteemY.
Resposta: D
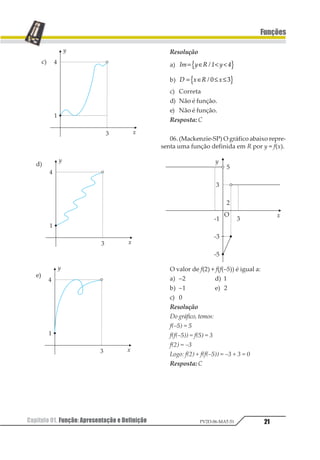
07. (UFMG) Das figuras abaixo, a única
que representa o gráfico de uma função real y
= f(x) com domínio [a, b] é:](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-14-320.jpg)

![Capítulo 01. Função: Apresentação e Definição18
Funções
PV2D-06-MAT-51
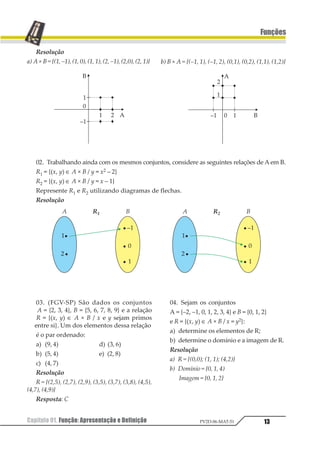
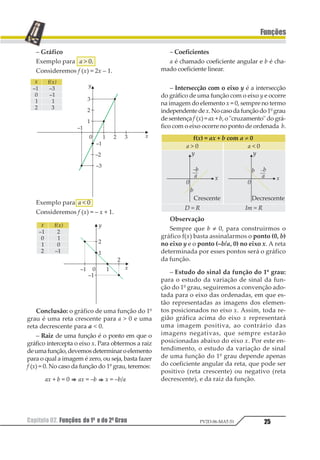
Vejamos o exemplo.
Consideremos a função real f(x) = 2x – 1.
Vamos construir uma tabela fornecendo
valores para x e, por meio da sentença f(x),
obteremos as imagens y correspondentes.
Transportados os pares ordenados para o
plano cartesiano, vamos obter o gráfico
correspondente à função f(x), como se vê a
seguir.
Podemos, por meio do gráfico de uma fun-
ção, reconhecer o seu domínio e o conjunto
imagem. Vamos observar o gráfico a seguir.
Consideremos a função f(x) definida por
A = [a, b] em R.
Domínio: projeção ortogonal do gráfico
da função no eixo x. Assim, D = [a, b] = A.
D = [a; b]
Conjunto imagem: projeção ortogonal do
gráfico da função no eixo y. Assim, Im = [c, d].](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-18-320.jpg)
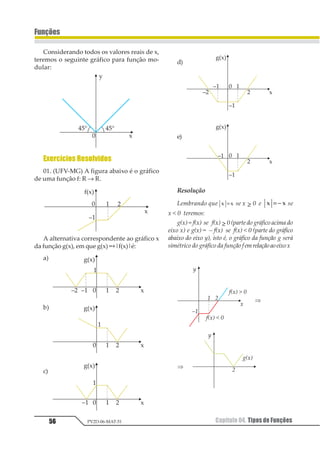
![Capítulo 01. Função: Apresentação e Definição 19
Funções
PV2D-06-MAT-51
Im = [c, d]
Observação
O contradomínio (R) é representado por
todo o eixo y.
Outra importante informação que pode-
mos retirar sobre o comportamento de uma
função, pela observação do gráfico, é a sua
monotonicidade. Uma função pode ter o se-
guinte comportamento:
I. função crescente: a função f(x), num de-
terminado intervalo, é crescente se, para
quaisquer x1 e x2 pertencentes a este interva-
lo, com x1 < x2, tivermos f(x1) < f(x2).
x1 < x2 ⇒ f(x1) < f(x2)
II. função decrescente: função f(x), num
determinado intervalo, é decrescente se, para
quaisquer x1 e x2 pertencentes a este interva-
lo, com x1 < x2, tivermos f(x1) > f(x2).
x1 < x2 ⇒ f(x1) > f(x2)
III. função constante: a função f(x), num
determinado intervalo, é constante se, para
quaisquer x1 e x2 pertencentes a este interva-
lo, com x1 < x2, tivermos f(x1) = f(x2).](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-19-320.jpg)




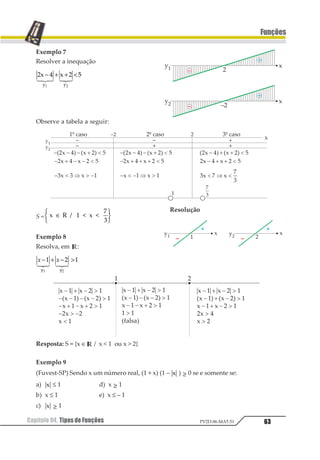
![Capítulo 02. Funções do 1º e do 2ºGrau 27
Funções
PV2D-06-MAT-51
04. Esboçar o gráfico, determinar o domínio,
contra-domínio, conjunto imagem e classificar
quanto ao crescimento as seguintes funções:
a) f(x) = 2x – 1
b) f(x) = 2 – x
c) f(x) = 2
Resolução
a) f(x) é uma função do 1º grau, então D = R,
CD = R e Im = R
Como a = 2 > 0, a função é crescente.
b) f(x) = 2 – x
f(x) é uma função do 1º grau, então D = R,
CD = R e Im = R.
Como a = –1 < 0, a função é decrescente.
c) f(x) = 2
f(x) é uma função constante, então D = R,
CD = R e Im = 2
05. (Unifor-CE) Seja f a função real definida
por 1 2
2
1 21 23
4
,paratodoxdointervalo[–3;1].
Seu conjunto imagem é:
a) R
b) −
1
23 4
56
1
2
13 d) −
1
23 4
56
1
2
3
2
4
c) −
1
23 4
56
1
2
1
2
3 e)
1
2
3
2
4
1
23 4
56
Resolução
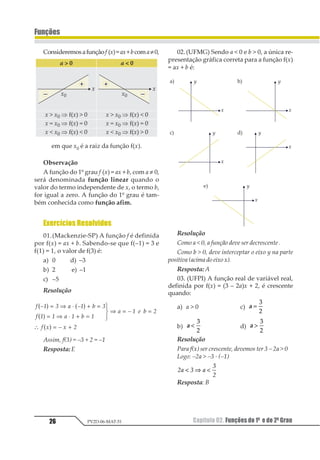
Como f(x) é do 1º grau, o gráfico seria uma reta.
Todavia, como o domínio é um intervalo real e não R,
o gráfico será um segmento de reta.
12 3 4 56 7 4
8
9
123
4
7 4
9
1
1
1
23
43
Logo,oconjuntoimagemserádefinidode
1
2
até
1
2
.
Assim:
12
3
4
5
6
4
=
1
23 4
56
Gráfico
Resposta: E](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-27-320.jpg)

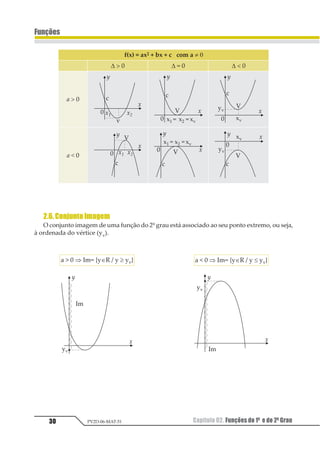
![Capítulo 02. Funções do 1º e do 2º Grau32
Funções
PV2D-06-MAT-51
02.(Vunesp) O gráfico da função
quadrática definida por y = x2 – mx + (m – 1),
onde m é um número real, tem um único ponto
em comum com o eixo das abscissas. Então o
valor de y que essa função associa a x = 2 é:
a) –2 d) 1
b) –1 e) 2
c) 0
Resolução
Como a função tem um único ponto em comum
com o eixo X, o valor de ∆ é zero. Assim:
∆ = 0 → (–m)2 –4 · 1 · (m – 1) = 0 → m = 2
Logo, y = x2 – 2x + 1. Portanto, para x = 2,
temos: y = 22 – 2 · 2 + 1 = 1
Resposta: D
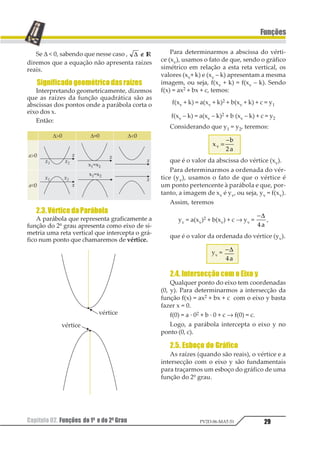
03. (UFRN) Se f(x) = x2 – 1, então é crescen-
te no intervalo:
a) [0, ∞[ d) ]–∞, 1]
b) [–1, 1] e) ]–∞, 0]
c) [–1, ∞[
Resolução
f(x) = x2 – 1
Esboçando o gráfico da função, temos:
Logo, a função é crescente para todo x ≥ 0.
Resposta: A
04.(UFPI) Uma fábrica produz p(t) = t2 + 2t
pares de sapatos t horas após o início de suas
atividades diárias. Se a fábrica começa a fun-
cionar às 8 horas da manhã, entre 10 e 11 ho-
ras serão produzidos:
a) 7 pares de sapatos.
b) 8 pares de sapatos.
c) 15 pares de sapatos.
d) 23 pares de sapatos.
Resolução
Para t = 3 horas, temos:
p(3) = 32 + 2 · 3 ⇒ p (3) = 15 pares de sapato
Para t = 2 horas, temos:
p(2) = 22 + 2 · 2 = 8 pares de sapato
Logo, entre 10 e 11 horas serão produzidos
15 – 8 = 7 pares de sapato.
Resposta: A
3. Função do 2º Grau: Pontos
Extremos
O gráfico da função do 2º grau
f(x) = ax2 + bx + c, a ≠ 0 é uma parábola. Essa
parábola tem a concavidade voltada para
cima quando a 0 e concavidade voltada para
baixo quando a 0.
3.1.VérticedaParábola
A parábola que representa graficamente
a função do 2º grau apresenta como eixo de
simetria uma reta vertical que intercepta o
gráfico num ponto chamado de vértice.
As coordenadas do vértice são:
1
2
3
1 =
−
4
e 1
2
1 =
−∆
3
3.2.ValoresExtremos
O yV representa o valor extremo da fun-
ção. Se a concavidade da parábola estiver vol-
tada para baixo, o yV será o valor máximo da
função; se a concavidade estiver voltada para
cima, o yV será o valor mínimo da função.](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-32-320.jpg)
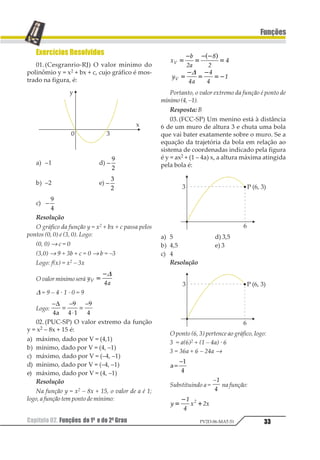








![Capítulo 03. Inequações do 1o e do 2o Grau 41
Funções
PV2D-06-MAT-51
t ≠ 1 e t ≠ 2
Resposta: D
04.(UCS-RS) O domínio da função
1 2 21 2= − +1
3 é:
a) [–2; 2] d) − 1 12
b) −1 121 2 e) − 1 121 2
c) −∞ − ∪ +∞1 12 21 2
Resolução
1 2 2 31
1 2= − +
Condição: –x2 + 2 ≥ 0
1 23 4 1 4 45 4∈ − ≤ ≤ = −1 2
Resposta: D
2. Inequação Produto
Chamamos de inequação produto toda
inequação resultante da multiplicação de ex-
pressões como (x – 1) · (x + 2) · (3 – x) 0. Nota-
mos não ser conveniente o desenvolvimento
da operação de multiplicação indicada, visto
que iríamos obter uma inequação do 3º grau de
difícil resolução. Por este motivo adotamos ou-
tro procedimento para a resolução deste tipo
de inequação, que será apresentado a seguir.
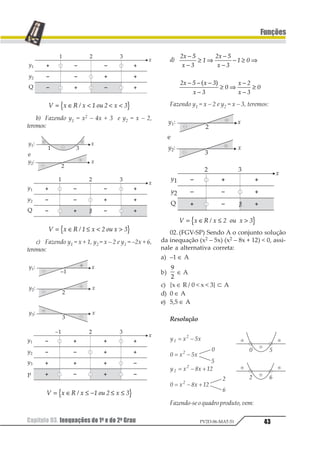
– Fazemos com que cada uma das expres-
sões (fatores do produto) seja associada a
uma função. Assim:
y1 = x – 1, y2 = x + 2 e y3 = 3 – x
– Estudamos a variação de sinal de cada
uma das funções de acordo com os seus
gráficos cartesianos.
y1
1
x
y2
–2
x
y3
3
x
– Reunimos estas variações de sinais num
quadro chamado quadro de sinais.
–2 3
y1
y2
P
y3
1
– Pela observação da última faixa do qua-
dro de sinais, que é onde aparece a varia-
ção de sinal do produto, podemos estabe-
lecer o cojunto solução da inequação:
S = 1 2 1 34 1∈ − 5 6 7 81 2
3. InequaçãoQuociente
Considerando que dois números não-nu-
los quando multiplicados apresentam o mes-
mo sinal que quando divididos, podemos re-
solver inequações fruto da divisão de duas
expressões pelo mesmo procedimento usado
para a resolução das inequações produto.
Exemplo
Resolver a inequação
1
1
+
−
≤
2
3
4.
– Fazemos com que cada uma das expres-
sões, tanto do numerador como denomi-
nador, seja associada a uma função. As-
sim:
y1 = x + 1 e y2 = x – 2](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-44-320.jpg)



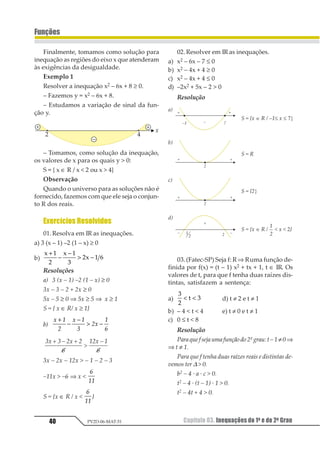
![Capítulo 04. Tipos de Funções 47
Funções
PV2D-06-MAT-51
Capítulo04.TiposdeFunções
1.FunçãoComposta
Consideremos duas funções reais (D = R e
CD = R), definidas pelas sentenças f(x) = 2x + 7
e g(x) = x2 – 1.
Vamos determinar, pelo uso da sentença
f(x), a imagem do elemento –2, ou seja,
f(–2) = 2 · (–2) + 7 = 3.
Agora, pelo uso da sentença g(x), vamos
determinar g(3) = 32 – 1 = 8.
Assim: g(3) = g [f(–2)] = 8.
Função composta de f e g é uma sentença
h capaz de diretamente conduzir o elemento
–2 até a imagem 8.
Só é possível compormos as funções g com
f se o conjunto da imagem f for o domínio da
função g.
1.1. Notação
A notação usual para indicar a composição
da função g(x) com a função f(x) é gof(x) – lê-se
“g bola f na variável x” ou “g círculo f na vari-
ável x” – mas podemos encontrar a indicação
apenas como gof ou um pouco mais sofisticada
(gof) (x). O importante é sabermos que:
gof(x) = g[(f(x)]
1.2. Determinação da Composta
Para exemplificar a determinação da fun-
ção composta, vamos utilizar as funções já
apresentadas:
f(x) = 2x + 7 e g(x) = x2 – 1
Assim:
gof(x) = g[f(x)] = f(x)2 – 1 = (2x + 7)2 – 1 = 4x2 +
+ 28x + 49 – 1 = gof(x) = 4x2 + 28x + 48
Aproveitando as mesmas duas funções e
ainda servindo como exemplo de determina-
ção da sentença que representa a composição
defunções,vamosdeterminarasentençafog(x).
Assim:
fog(x) = f[g(x)] = 2 g(x) + 7 = 2(x2 – 1) + 7 =
= 2x2 – 2 + 7 = fog (x) = 2x2 + 5
É bom compararmos esses dois exemplos
de composição de funções para notarmos que
a composição não admite a propriedade
comutativa, ou seja, em geral fog ≠≠≠≠≠ gof.
Exercícios Resolvidos
01. (AMAN-RJ) Se f(x) = 3x + 1 e g(x) = 2x2,
então f [g(–1)] – g [f(–1)] é igual a:
a) –1 d) 0
b) 1 e) nra.
c) 15
Resolução
Cálculos auxiliares:
g(–1) = 2 (–1)2 = 2
f(–1) = 3 (–1) + 1 = –2
f[g(–1)] = f(2) = 3 · 2 + 1 = 7
g[f(–1)] = g[–2] = 2 (–2)2 = 8
Logo:
f[g(–1)] – g[f(–1)] = 7 – 8 = –1
Resposta: A
02. (EESC-SP) Se f(x) = x2 e g(x) = x3, então
f[g(2)] é:
a) 16 d) 64
b) 128 e) 32
c) 12](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-51-320.jpg)
![Capítulo 04. Tipos de Funções48
Funções
PV2D-06-MAT-51
Resolução
f [g(2)] = f(23) = f(8) = 82 = 64
Resposta: D
03.(FGV-SP) Considere as funções
f(x) = 2x + 1 e g(x) = x2 – 1. Então, as raízes da
equação f[g(x)] = 0 são:
a) inteiras.
b) negativas.
c) racionais não inteiras.
d) inversas uma da outra.
e) opostas.
Resolução
f[g(x)] = 0 ⇒ f [x2 – 1] = 0
2 (x2 – 1) + 1 = 0 ⇒ 2x2 – 2 + 1 = 0
2x2 = 1 ⇒ x2 =
1
2
⇒ x = ±
1
2
⇒ x = ±
1
1
Logo, as raízes são opostas.
Resposta: E
04.Considerando que f(x) = x + 2 e f[g(x)] =
2x – 3, então g(x) é igual a:
a) 5 – x d) x2
b) 4x – 2 e) 2 – 4x
c) 2x – 5
Resolução
f [g(x)] = g(x) + 2
2x – 3 = g(x) + 2 ⇒ g(x) = 2x – 5
Resposta: C
05.Sendo g(x) = x – 7 e f[g(x)] = 3x – 1, de-
terminar a função f(x).
Resolução
g(x) = x – 7 ⇒ x = g(x) + 7
f[g(x)] = 3x – 1 ⇒ f[g(x)] = 3[g(x) + 7] – 1
f [g(x)] = 3g(x) + 20 ⇒ f(x) = 3x + 20
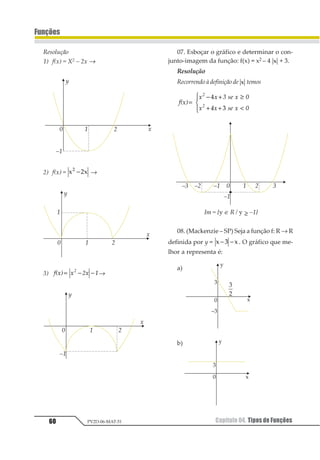
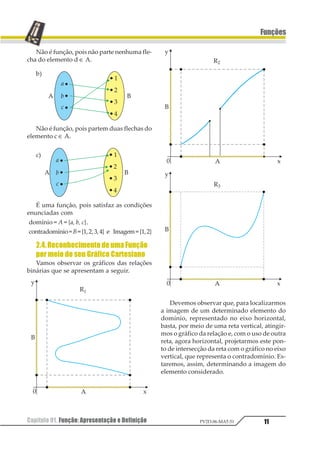
2.Classificação
2.1. Injetora
Uma função é chamada injetora quando
para ela elementos distintos do domínio apre-
sentarem imagens também distintas no con-
tra-domínio.
x1 ≠ x2 ⇒ f(x1) ≠ f(x2)
Reconhecemos, graficamente, uma função
injetora quando, uma reta horizontal, qual-
quer que seja, interceptar o gráfico da função,
uma única vez.
f(x) é injetora
g(x) não é injetora
(interceptou o gráfico mais de uma vez)](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-52-320.jpg)
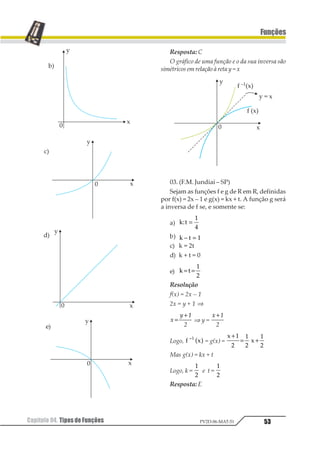
![Capítulo 04. Tipos de Funções50
Funções
PV2D-06-MAT-51
Exercícios Resolvidos
01.Os gráficos abaixo representam fun-
ções de R em R.
Verifique se elas são ou não sobrejetoras,
injetoras ou bijetoras. Justifique.
Resolução
a) D (f) = R
Im (f) = {3}
CD (f) = R
Não é sobrejetora, pois Im (f) ≠ CD (f) = R
Não é injetora, pois todos os elementos do
domíniotêmcomoimagemoelemento3.
Como não é injetora nem sobrejetora, não é
bijetora.
b) D (f) = R
Im (f) = R
CD (f) = R
É sobrejetora, pois Im (f) = CD (f).
Éinjetora,poistodososelementosdistintosx
do domínio têm imagens g distintas do
contradomínio.
Logo, é bijetora.
c) D (f) = R
Im (f) = 1 231
4
5
∈ ≥ −
123
456
CD (f) = R
Não é sobrejetora, pois Im(f) ≠ CD (f).
Nãoéinjetora,poisexistemelementosdeIm(f)
quesãoimagemdedoisvaloresdistintosdex.
Logo, não é bijetora.
02.Determinar o conjunto B de modo que
a sentença f(x) = x2 defina uma função
sobrejetora de A = { x ∈ R / –3 ≤ x ≤ 4} em B.
Dizer se, nessas condições, ela é bijetora.
Resolução
B = CD = Im [y ∈ R / 0 ≤ y ≤ 16]
Não é bijetora, pois não é injetora.
3. Função Inversa
3.1.Conceito
Vamos considerar uma função f com do-
mínio A e contradomínio B para a qual cada
elemento x pertencente ao conjunto A apre-
senta uma imagem y = f(x) pertencente ao
conjunto B. Podemos pensar na existência de
uma função que a partir da imagem y deter-
mine o elemento x, ou seja, uma função g tal](https://image.slidesharecdn.com/mat05-livro-teoria-161018151743/85/Funcoes-Teoria-54-320.jpg)