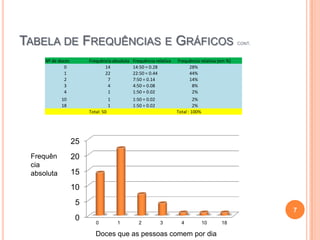
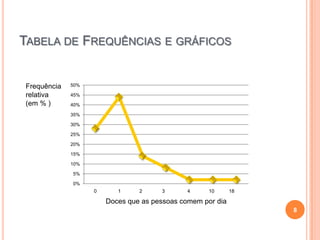
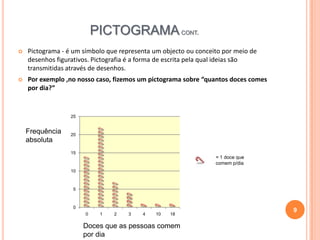
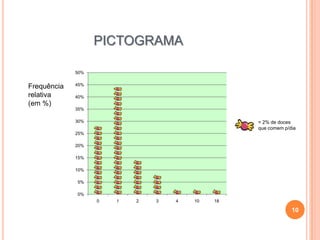
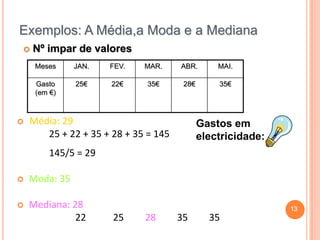
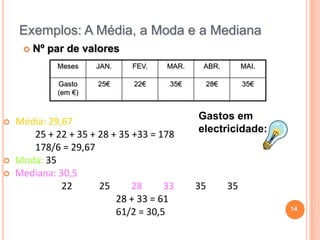
O documento fornece uma introdução sobre estatística, descrevendo o que é estatística, como surgiu, e para que serve. Inclui exemplos de tabelas de frequências, gráficos, média, moda e mediana. Conclui com curiosidades sobre estatística e uma breve bibliografia.

1. MATEMÁTICA
Estatística

2. ÍNDICE

Introdução (pág.3)

O que é a Estatística? (pág.4)

Como apareceu a Estatística? (pág.5)

Para que serve a Estatística? (pág.6)

Tabela de Frequências e Gráficos cont. (pág.7)

Tabela de Frequências e Gráficos (pág.8)

Pictograma (pág.9 e 10)

A Média ,a Moda e a Mediana (pág.11)

Situações aleatórias (pág.12)

Exemplos: A Média, a Moda e a Mediana(pág.13)

Exemplos: A Média, a Moda e a Mediana (pág. 14)

Questionário e Respostas (pág.15)

Curiosidades (pág.16)

Conclusão (pág.17)

Bibliografia (pág.18)
2

3. INTRODUÇÃO

A estatística é, hoje em dia, um instrumento útil e, nalguns casos, indispensável
para tomadas de decisão em diversos campos: científico, económico, social,
político…

A Estatística constitui um ramo da Matemática que se desenvolveu apenas a
partir do início do século passado. No entanto, apesar de recente, esta área é de
uma extraordinária importância e tem aplicações variadas. Para além da sua
aplicação mais formal, a Estatística está constantemente a ser usada no dia-a-dia,
na sociedade, para veicular informação nos órgãos de comunicação, para
fundamentar a tomada de decisões, etc.
3

4. O QUE É A ESTATÍSTICA?
A Estatística significa enumeração ou informação numérica habitualmente contida em tabelas
ou gráficos. Quando se fala em Estatística pensa-se em censos, inventários, amostras ou
médias. Em sentido restrito tudo isso se pode considerar uma Estatística.
A Estatística é uma ciência exacta que refere-se a fornecer subsídios ao analista para colectar,
organizar, resumir, analisar e apresentar dados.
Hoje em dia, no nosso dia-a-dia, precisamos de tomar decisões, muitas vezes decisões rápidas.
Existem dois tipos de Estatística diferentes:
A Estatística Descritiva que é responsável pelo estudo das características de uma dada
população; e
A Estatística Indutiva, que generaliza um conjunto de resultados, tendo por base uma amostra
de uma dada população ou universo, enunciando a(s) consequente(s) lei(s).
4

5. COMO APARECEU A ESTATÍSTICA?

As necessidades que exigiam o conhecimento numérico dos recursos disponíveis
começaram a surgir quando as sociedades primitivas se organizaram. Os Estados,
desde tempos remotos, precisaram conhecer determinadas características da
população, efectuar a sua contagem e saber a sua composição ou os seus
rendimentos.

Para que os governantes das grandes civilizações antigas tivessem conhecimento
dos bens que o Estado possuía e como estavam distribuídos pelos habitantes,
realizaram-se as primeiras estatísticas, nomeadamente para determinarem leis
sobre impostos e números de homens disponíveis para combater. Estas estatísticas,
eram frequentemente limitadas à população masculina.

Ao longo da Idade Média e até ao século XVIII a estatística foi puramente
descritiva, concorrendo duas escolas: a escola descritiva alemã, cujo representante
mais conhecido é o economista G. Achenwall (1719-1772), professor na
Universidade de Gottingen, considerado pelos alemães como o “pai da estatística”,
e a escola dos matemáticos sociais que procuravam traduzir por leis a regularidade
observada de certos fenómenos, de carácter económico e sociológico.
5

6. PARA QUE SERVE A ESTATÍSTICA?



A estatística fornece-nos as técnicas para extrair informação de dados, os quais são muitas
vezes incompletos, na medida em que nos dão informação útil sobre o problema em
estudo, sendo assim, é objectivo da Estatística extrair informação dos dados para obter
uma melhor compreensão das situações que representam.
A Estatística é muito importante nas mais diversas áreas, e diria que em todas as áreas, ela
è importante, pois através da analise de gráficos estatísticos, cientistas, estudiosos e
políticos, podem prever algumas situações e assim agir preventivamente no futuro, para
alterar os dados dos próximos tráficos, se os anteriores forem negativos.
Exemplos: através dos gráficos estatísticos, de casos de dengue, pode-se entender se em
determinada região, tem uma epidemia, e sendo assim tomar providencias para que esta
epidemia acabe ou não se expanda a outras regiões. Por isso è muito importante que os
casos de dengue, assim como todas doenças transmissíveis, sejam notificadas no posto de
saúde. Se não forem notificadas os responsáveis pela saúde, têm sempre a desculpa dos
números oficiais dados pelo centro de saúde ( isto é dos casos notificados). Da mesma
forma, os casos de assaltos, furtos de carro, roubos de casa, que muitas vezes as pessoas
não denunciam na policia, pois se conformam dizendo que não serve para nada, e
realmente não serve para nada, mas serve apara aumentar a estatística, pois os políticos
usam estes dados para mostrar que os crimes não são iguais a todas as grandes cidades do
mundo etc... é que nas grandes cidades de países desenvolvidos, todo mundo denuncia os
furtos e crimes. Mais um exemplo : com o gráfico estatístico do numero de turistas
estrangeiros que visitam uma determinada cidade, pode-se planear a necessidade ou não
de se abrir uma agencia de cambio, ou de guias turísticos multilingue.
6

7. TABELA DE FREQUÊNCIAS E GRÁFICOS
Nº de doces
0
1
2
3
4
Frequência absoluta
14
22
7
4
1
10
18
Frequência relativa (em %)
28%
44%
14%
8%
2%
1:50 = 0.02
1:50 = 0.02
1
1
Frequência relativa
14:50 = 0.28
22:50 = 0.44
7:50 = 0.14
4:50 = 0.08
1:50 = 0.02
CONT.
2%
2%
Total : 100%
Total: 50
25
Frequên
cia
absoluta
20
15
10
5
7
0
0
1
2
3
4
10
Doces que as pessoas comem por dia
18

8. TABELA DE FREQUÊNCIAS E GRÁFICOS
Frequência
relativa
(em % )
50%
45%
40%
35%
30%
25%
20%
15%
10%
5%
0%
0
1
2
3
4
10
18
Doces que as pessoas comem por dia
8

9. PICTOGRAMA CONT.

Pictograma - é um símbolo que representa um objecto ou conceito por meio de
desenhos figurativos. Pictografia é a forma de escrita pela qual ideias são
transmitidas através de desenhos.

Por exemplo ,no nosso caso, fizemos um pictograma sobre “quantos doces comes
por dia?”
25
Frequência
absoluta
20
15
= 1 doce que
comem p/dia
10
5
0
0
1
2
3
4
10
18
Doces que as pessoas comem
por dia
9

10. PICTOGRAMA
50%
Frequência
relativa
(em %)
45%
40%
35%
30%
= 2% de doces
que comem p/dia
25%
20%
15%
10%
5%
0%
0
1
2
3
4
10
18
10

11. A Média, a Moda e a Mediana

A Média de um conjunto de dados numéricos obtém-se somando os valores de todos os dados e
dividindo a soma pelo número de dados

Exº : Média = 0x14 + 1x22 + 2x7 + 3x4 + 4x1 + 10x1 + 18x1 =
50


Média = 0 + 22 + 14 + 12 + 4 + 10 + 18 = 80:50 = 1.6
50


Nota: só podemos calcular a média se as respostas forem dados numéricos

A Moda é o valor mais frequente que aparece num conjunto de dados.

Neste caso a moda é “um doce”, porque foi a resposta a que a maioria das pessoas
responderam.

Como só existe uma moda , chamamos a este estudo estatística é unimodal; se tivesse duas
modas chamava-se bimodal , se tivesse mais de duas modas chamava-se multimodal e , se não
existe moda, chamava-se amodal.

Mediana:
Depois de ordenados os valores por ordem crescente ou decrescente, a mediana é:
-o valor que ocupa a posição central, se a quantidade desses valores for ímpar;
- a média dos dois valores centrais, se a quantidade desses valores for par.
Estas Técnicas pertencem à Estatística Descritiva são aplicadas para descrever e resumir um
conjunto de dados.
11

12. SITUAÇÕES ALEATÓRIAS
 Certo – É certo as pessoas responderem 0,1,2,4,10 e 18 doces que
comem por dia.

Muito provável – É muito provável as pessoas responderm 0 e 1
doces que comem por dia.

Pouco provável – É pouco provável as pessoas responderem 10 ou
18 doces que comem por dia.

Impossível – É impossível as pessoas responderem 20 doces que
comem por dia.
12

13. Exemplos: A Média,a Moda e a Mediana

Nº impar de valores
Meses
FEV.
MAR.
ABR.
MAI.
Gasto
(em €)

JAN.
25€
22€
35€
28€
35€
Média: 29
25 + 22 + 35 + 28 + 35 = 145
Gastos em
electricidade:
145/5 = 29

Moda: 35

Mediana: 28
22
13
25
28
35
35

14. Exemplos: A Média, a Moda e a Mediana

Nº par de valores
Meses


FEV.
MAR.
ABR.
MAI.
Gasto
(em €)

JAN.
25€
22€
35€
28€
35€
Média: 29,67
25 + 22 + 35 + 28 + 35 +33 = 178
178/6 = 29,67
Moda: 35
Mediana: 30,5
22
25
28
33
28 + 33 = 61
61/2 = 30,5
Gastos em
electricidade:
35
35
14

15. QUESTIONÁRIO E RESPOSTAS
Qual o número de computadores vendidos no 1º
trimestre?
 Qual o trimestre em que se venderam mais
computadores?
 Qual o número de computadores vendidos este
ano?
 Qual a média de computadores vendidos nos
quatro trimestres?

RESPOSTAS
25«

100

15
4

15


16. CURIOSIDADES

A palavra Estatística surge, pela primeira vez, no séc. XVIII. Alguns autores atribuem
esta origem ao alemão Gottfried Achemmel (1719-1772), que teria utilizado pela
primeira vez o termo statistik, do grego statizein; outros dizem ter origem na palavra
estado, do latim status, pelo aproveitamento que dela tiravam os políticos e o
Estado.

O primeiro dado disponível sobre um levantamento estatístico foi referido por
Heródoto, que afirmava ter-se efectuado em 3050 a. C. um estudo das riquezas da
população do Egipto com a finalidade de averiguar quais os recursos humanos e
económicos disponíveis para a construção das pirâmides.

Há também notícia de que no ano 2238 a. C. se realizou um levantamento estatístico
com fins industriais e comerciais ordenado pelo imperador chinês Yao.
16

17. CONCLUSÃO

A estatística é a ciência das probabilidades , o conjunto de regras matemáticas que
permite fazer previsões sobre determinado universo estudado, a partir de uma
amostragem significativa .

A estatística é uma ciência não exacta.

Hoje em dia a Estatística está em todo o lado, de diferentes formas. A partir de
agora, espero que quando lerem uma notícia que envolva alguma coisa sobre
estatística, num jornal ou numa revista, estejam de olhos bem abertos para
pormenores que antes não tinham importância por não os conhecerem.
17

18. BIBLIOGRAFIA

http://www.notapositiva.com/trab_estudantes/trab_estudantes/matematica/mate
matica_trabalhos/estatistica.htm

http://www.educ.fc.ul.pt/icm/icm2003/icm24/introducao.htm

http://pt.wikipedia.org/wiki/Estat%C3%ADstica

http://www.mundoeducacao.com.br/matematica/estatistica.htm

http://www.brasilescola.com/matematica/estatistica-1.htm

http://br.answers.yahoo.com/question/index?qid=20070603141047AAprHCh

http://www.eccn.edu.pt/webquests/wq_soniamedeiros/conclusao.htm

http://pt.wikipedia.org/wiki/Estat%C3%ADstica

http://www.antoniolima.web.br.com/arquivos/estatistica.htm

Caderno Diário de Matemática

Neves, M.A.F, Faria, L. e Silva, J.N. (2010) Matemática – Parte 3 . Porto: Porto Editora
18