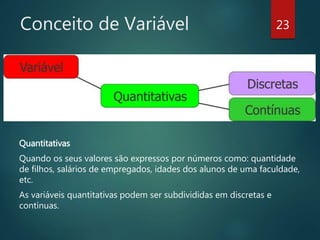
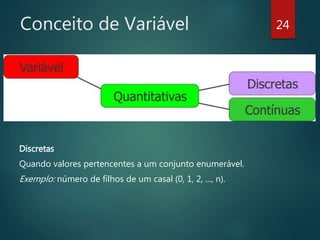
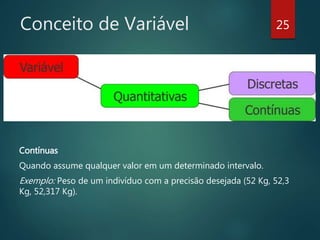
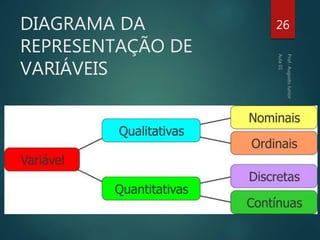
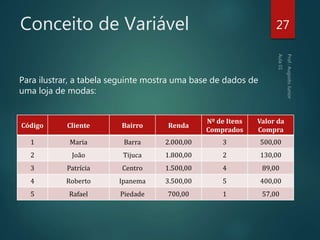
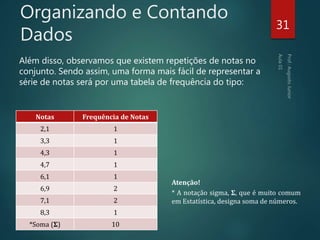
O documento fornece uma introdução à estatística, abordando seus objetivos, uma breve história da estatística, as principais classificações da estatística (descritiva, probabilidades e inferencial), conceitos importantes como população e amostra, tipos de variáveis, organização e contagem de dados, e exercícios de fixação.

1. Probabilidade e
Estatística
INTRODUÇÃO À ESTATÍSTICA
1

2. Objetivos
 Conhecer um panorama histórico e a natureza da
Estatística;
 Entender a importância da Estatística como uma poderosa
ferramenta de análise de dados para tomada de decisões e
a sua utilização em diversos tipos de pesquisas;
 Identificar as diferenças entre os três ramos da Estatística: a
Descritiva, das Probabilidades e a Inferencial;
 Diferenciar uma população de uma amostra;
 Classificar os tipos de dados em uma função de seus níveis
de informação;
 Começar a organizar os dados de um fenômeno coletivo de
forma eficiente.
2

3. A Natureza da Estatística –
Um Panorama Histórico
Antiguidade
Na Antiguidade, os povos já sentiam a necessidade de um
desenvolvimento social, registravam o número de habitantes,
de nascimentos, de óbitos, faziam estimativas das riquezas
individuais e sociais.
Embora não existisse ainda a palavra Estatística, existem
indícios de que há 3000 anos a.C. já se faziam censos na
Babilônia, China e Egito.
3

4. A Natureza da Estatística –
Um Panorama Histórico
Bíblia
 O livro quarto do Velho Testamento, intitulado “Números”,
começa com a seguinte instrução à Moisés: “-Fazer um
levantamento dos homens de Israel que estivessem aptos
para guerrear.”
 O Imperador Herodes pediu para que se fizesse o censo em
todo o Império para motivos excusos. Por isso, Maria e José
saíram da cidade e viajaram para Belém.
Idade Média
 Já na Idade Média, estatísticas foram feitas com finalidades
de cobranças de impostos e para recenseamento militar.
4

5. A Natureza da Estatística –
Um Panorama Histórico
 A Estatística teve origem na necessidade do Estado Político
em conhecer os seus domínios.
 A palavra, provavelmente derivada da palavra “status”
(estado, em latim), acumularam-se descrições e dados
relativos ao Estado.
 Nas mãos dos governantes, passou a constituir-se de uma
verdadeira ferramenta administrativa.
5

6. A Natureza da Estatística –
Um Panorama Histórico
 Em 1085, Guilherme I – O
Conquistador – ordenou que se
fizesse um levantamento
estatístico na Inglaterra.
 Informações como terras,
proprietários, uso da terra,
empregados, animais.
 Uso para o cálculo de impostos.
 Esse levantamento originou um
volume, intitulado “Domesday
Book” (Livro do dia do juízo final)
6

7. A Natureza da Estatística –
Um Panorama Histórico
Século XVII
 Século de destaque da Estatística
na Inglaterra.
 Jonh Graunt e William Petty:
Tábuas de mortalidade
 Aritmética política, que consistiu
exaustivas análises de nascimentos
e mortes.
 Principal conclusão desse trabalho:
 O percentual de nascimentos de
indivíduos do sexo masculino era
ligeiramente maior que do sexo
feminino.
7

8. A Natureza da Estatística –
Um Panorama Histórico
Século XVIII
 1708: Organizado o primeiro curso
de Estatística na Universade de
Yena, na Alemanha;
 1740: Gottfried Achenwall, sugeriu
o nome de "Estatística" para esta
nova Ciência, determinando quais
eram os seus objetivos e relações
com as demais Ciências.
8

9. A Natureza da Estatística –
Um Panorama Histórico
 Contudo, foi o casamento entre o cálculo das
probabilidades e a estatística, em meados do século XIX,
que permitiu que a Estatística fosse melhor estruturada e
ampliasse o seu campo de ação.
 O avanço na teoria das probabilidades possibilitou a
descoberta das distribuições de probabilidade.
 Consequência: criação de técnicas de amostragens mais
adequadas e início da relação das amostras com as populações
de onde vieram.
 Séculos XX e XXI: Computação eletrônica
 Pacotes estatísticos como o Statistica, Stata, SAS, Eviews, R-
Project e outros se tornaram populares e vem ajudando no
processamento das informações.
9

10. O que é Estatística?
É a Ciência que estuda método de
coleta, organização, descrição, análise
e interpretação de dados, para a
obtenção de conclusões válidas e
tomadas de decisões.
10

11. Classificação das Estatísticas
 Estatística Descritiva
Cuida do resumo e apresentação dos dados observados por
meio de tabelas, gráficos e medidas, sem se preocupar com as
populações de onde foram tirados os dados.
 Inferência Estatística
Fornecer métodos para possibilitar a inferência sobre
populações a partir de amostras delas provenientes.
Tem como base o cálculo de probabilidades e compreende
dois grandes tópicos: a estimação de parâmetros e os testes de
hipóteses.
11

12. Classificação das Estatísticas
 Embora a estatística descritiva seja um ramo fundamental, em
muitos casos ela não é suficiente.
 Informações obtidas de amostras;
 A análise requer generalizações que ultrapassam os dados
disponíveis.
 Essa necessidade, aliada ao desenvolvimento dos métodos
probabilísticos, promoveu o crescimento da estatística,
agregando os métodos generalizadores (Inferência Estatística).
 Exemplos que ilustram a necessidade desses métodos
generalizadores:
 Prever o tempo de vida útil de uma calculadora, com base no
desempenho de várias dessa calculadora;
 Comparar a eficiência de duas dietas para reduzir peso, com base na
perda de peso de pessoas que se submeteram às dietas;
 Determinar a dosagem ideal de um medicamento novo, com base
em testes feitos em pacientes voluntários de hospitais selecionados
aleatoriamente;
 Prever o fluxo de tráfego de uma rodovia ainda em construção, com
no tráfego observado em rodovias alternativas.
12

13. Aplicações da Estatística
Algumas das aplicações da Estatística em algumas situações
distintas e sua influência em processos decisórios.
 Na Saúde: Fornece metodologia adequada que possibilita
decidir sobre a eficiência de um novo tratamento no
combate à uma doença.
 Na Política: Utiliza-se de pesquisas prévias de opiniões para
muitas vezes corrigir estratégias de campanha para uma
determinada ação.
 No Controle de Qualidade: Testa a reação de um grupo de
consumidores sobre um novo produto e com base nas
respostas decidem-se pela sua produção e distribuição em
uma escala nacional.
13

14. Aplicações da Estatística
 Na Mídia: Calcula índices de audiência de um determinado
canal e em um determinado horário, para estabelecer o
preço a ser cobrado aos anunciantes pela veiculação de
suas propagandas.
 Em Marketing: Testa a reação de um grupo de
consumidores sobre um novo produto e com base nas
respostas decidem-se pela sua produção e distribuição em
uma escala nacional.
 Em Finanças: Observa índices de inflação, emprego e
desemprego para estimar alguns aspectos econômicos do
cenário nacional.
14

15. População e Amostra
Ao conjunto ou grupo de indivíduos que possuem pelo menos
uma característica em comum, denominamos de população
estatística ou de universo estatístico.
Exemplos:
 Estudantes constituem uma população, pois apresentam
pelo menos uma característica em comum: são os que
estudam.
 Os brasileiros que votaram nas últimas eleições.
 As peças produzidas em um determinado setor de uma
indústria no mês passado.
15

16. População e Amostra
Uma Amostra é um subconjunto finito não vazio de uma
população estatística.
Exemplos:
 Apenas estudantes universitários.
 Apenas os eleitores do Sul do país.
 Apenas peças produzidas na última semana do mês.
Para obtermos previsões válidas sobre um determinado
problema quase nunca utilizamos todos os elementos da
população, trabalhamos apenas com amostras desta
população.
16

17. População e Amostra
Exemplo - Previsão baseada em amostra
Antes de uma eleição, os institutos de pesquisa entrevistaram
2000 pessoas e, com base em suas respostas, conseguem
prever o resultado da eleição.
17

18. Conceito de Variável
Para cada experimento ou informação, obtemos um número
de resultados possíveis, por exemplo:
 Se o experimento refere-se a uma categoria como "gênero
de uma pessoa" são dois os resultados possíveis: masculino
ou feminino.
 Se o experimento refere-se a uma categoria como "estatura
de uma pessoa" temos vários resultados possíveis dentro
de um intervalo de números.
18

19. Conceito de Variável
Variável
É o conjunto de resultados possíveis de um experimento ou
informação.
Dependendo dos dados coletados em um experimento as variáveis
podem ser classificadas em qualitativas e quantitativas.
19

20. Conceito de Variável
Qualitativas
Quando os seus valores são expressos por um atributo como: gênero
(masculino ou feminino); cor da pele (branco, pardo, amarelo, preto);
estatura (alto, médio, baixo).
As variáveis qualitativas podem ser subdivididas em nominais e
ordinais.
20

21. Conceito de Variável
Nominais
Quando não permitem comparações.
Exemplos: o nome ou o gênero de um indivíduo (João ou Maria;
masculino ou feminino).
Não é possível estabelecer qual a prioridade ou o mais importante
nessas características.
21

22. Conceito de Variável
Ordinais
Quando permitem comparações.
Exemplo: Atribuição de status (alto, médio ou baixo) para um indivíduo.
É possível estabelecer comparações de intensidade e ordenamento.
22

23. Conceito de Variável
Quantitativas
Quando os seus valores são expressos por números como: quantidade
de filhos, salários de empregados, idades dos alunos de uma faculdade,
etc.
As variáveis quantitativas podem ser subdivididas em discretas e
contínuas.
23

24. Conceito de Variável
Discretas
Quando valores pertencentes a um conjunto enumerável.
Exemplo: número de filhos de um casal (0, 1, 2, ..., n).
24

25. Conceito de Variável
Contínuas
Quando assume qualquer valor em um determinado intervalo.
Exemplo: Peso de um indivíduo com a precisão desejada (52 Kg, 52,3
Kg, 52,317 Kg).
25

26. DIAGRAMA DA
REPRESENTAÇÃO DE
VARIÁVEIS
26

27. Conceito de Variável
Para ilustrar, a tabela seguinte mostra uma base de dados de
uma loja de modas:
27
Código Cliente Bairro Renda
Nº de Itens
Comprados
Valor da
Compra
1 Maria Barra 2.000,00 3 500,00
2 João Tijuca 1.800,00 2 130,00
3 Patrícia Centro 1.500,00 4 89,00
4 Roberto Ipanema 3.500,00 5 400,00
5 Rafael Piedade 700,00 1 57,00

28. Conceito de Variável
A classificação das seis variáveis apresentadas a seguir:
28
Variável Classificação
Código Qualitativa nominal
Cliente Qualitativa nominal
Bairro Qualitativa nominal
Renda Quantitativa contínua
Nº de Itens Comprados Quantitativa discreta
Valor da Compra Quantitativa contínua

29. Organizando e Contando
Dados
Os dados coletados da observação de um fenômeno coletivo,
sem manipulação ou ordenação, são chamados de dados
brutos.
Exemplo:
As notas de matemática de um grupo de alunos ao final da
primeira avaliação são:
2,1; 7,1; 4,3; 3,3; 4,7; 6,9; 6,1; 7,1; 8,3; 6,9.
A série numérica exposta poderia ser de melhor forma
apresentada se estabelecêssemos uma ordenação para as
notas. Esta etapa consiste na elaboração de um Rol ou
conjunto ordenado de dados.
29

30. Organizando e Contando
Dados
Um tipo de Rol para esta série de notas poderia ser colocá-las
em ordem crescente na forma:
{2,1; 3,3; 4,3; 4,7; 6,1; 6,9; 6,9; 7,1; 7,1; 8,3}
Além de visualizar melhor a série o Rol evidência os seus
valores extremos (maiores e menores notas).
“Neste ponto vale comentar que as presenças de valores
extremos em conjuntos de dados distorcem a maior parte das
medidas estatísticas obtidas. Esta discussão será abordada com
mais profundidade em materiais futuros”.
30

31. Organizando e Contando
Dados
Além disso, observamos que existem repetições de notas no
conjunto. Sendo assim, uma forma mais fácil de representar a
série de notas será por uma tabela de frequência do tipo:
31
Notas Frequência de Notas
2,1 1
3,3 1
4,3 1
4,7 1
6,1 1
6,9 2
7,1 2
8,3 1
*Soma (Σ) 10
Atenção!
* A notação sigma, Σ, que é muito comum
em Estatística, designa soma de números.

32. Introdução à
Estatística
EXERCÍCIOS DE FIXAÇÃO
32

33. Exercícios de Fixação
1. A parcela da população convenientemente escolhida
para representa-la é chamada de:
a) Variável.
b) Rol.
c) Amostra.
d) Dados Brutos.
e) Nada podemos afirmar, a informação é incompleta.
33

34. Exercícios de Fixação
1. A parcela da população convenientemente escolhida
para representa-la é chamada de:
a) Variável.
b) Rol.
c) Amostra.
d) Dados Brutos.
e) Nada podemos afirmar, a informação é incompleta.
34

35. Exercícios de Fixação
2. Ao nascer os bebês são pesados e medidos, para se
saber se estão dentro das tabelas de peso e altura
esperados. Estas duas variáveis são:
a) Qualitativas.
b) Discretas.
c) Contínuas.
d) Contínua e Discreta, respectivamente.
e) Discreta e Contínua, respectivamente.
35

36. Exercícios de Fixação
2. Ao nascer os bebês são pesados e medidos, para se
saber se estão dentro das tabelas de peso e altura
esperados. Estas duas variáveis são:
a) Qualitativas.
b) Discretas.
c) Contínuas.
d) Contínua e Discreta, respectivamente.
e) Discreta e Contínua, respectivamente.
36

37. Exercícios de Fixação
3. Por definição, o rol é qualquer sequência ordenada de valores
referentes a uma mesma variável. Então, dadas as sequências da
mesma variável x:
I. -2, 4, 5, 6, 7.
II. 1, 3, 3, 6, 7
III. 8, 7, 5, 2, 1.
IV. 5, 4, 4, -1.
podemos afirmar que:
a) Todas elas constituem róis.
b) Só a sequência I constitui rol.
c) A sequência II não é um rol, mas as outras sim.
d) Apenas as sequências I e IV são róis.
e) Somente a sequência III é um rol, as demais não.
37

38. Exercícios de Fixação
3. Por definição, o rol é qualquer sequência ordenada de valores
referentes a uma mesma variável. Então, dadas as sequências da
mesma variável x:
I. -2, 4, 5, 6, 7.
II. 1, 3, 3, 6, 7
III. 8, 7, 5, 2, 1.
IV. 5, 4, 4, -1.
podemos afirmar que:
a) Todas elas constituem róis.
b) Só a sequência I constitui rol.
c) A sequência II não é um rol, mas as outras sim.
d) Apenas as sequências I e IV são róis.
e) Somente a sequência III é um rol, as demais não.
38

39. Exercícios de Fixação
4. O método estatístico tem como um dos seus fins:
a) Estudar os fenômenos estatísticos.
b) Estudar qualidades concretas dos indivíduos que
formam grupos.
c) Determinar qualidades abstratas dos indivíduos que
formam grupos.
d) Determinar qualidades abstratas de grupos de
indivíduos.
e) Estudar fenômenos numéricos.
39

40. Exercícios de Fixação
4. O método estatístico tem como um dos seus fins:
a) Estudar os fenômenos estatísticos.
b) Estudar qualidades concretas dos indivíduos que
formam grupos.
c) Determinar qualidades abstratas dos indivíduos que
formam grupos.
d) Determinar qualidades abstratas de grupos de
indivíduos.
e) Estudar fenômenos numéricos.
40

41. Introdução à
Estatística
EXTRAS
41

42. Links
 Para pesquisa e obtenção de dados e tabelas
estatísticas do Instituto de Planejamento Urbano de
Curitiba - www.ippuc.org.br
 Para informações educacionais do Instituto Nacional
de Estudos Educacionais - www.inep.gov.br
42