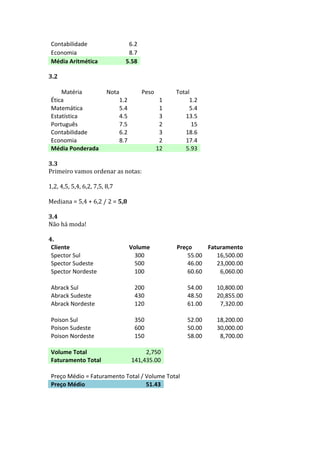
O documento apresenta 10 exercícios de estatística envolvendo distribuição de frequência, medidas de tendência central, probabilidade e outros conceitos. Os exercícios solicitam o cálculo de medidas como média, mediana, moda, quartis, probabilidades e índices numéricos com base em tabelas de dados sobre pesos de jogadoras, notas de alunos, vendas de produtos, salários e outros.