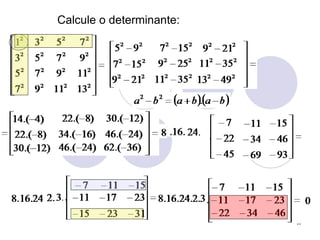
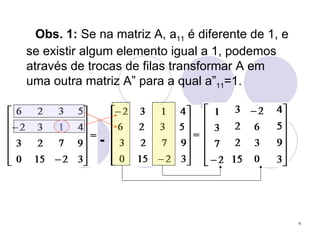
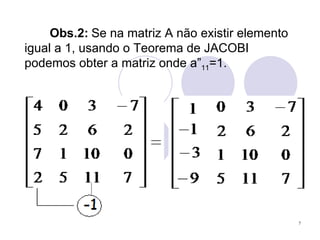
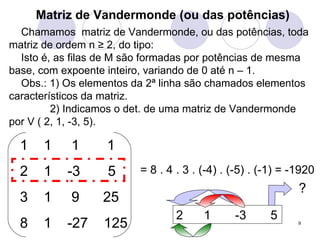
1) O documento apresenta as regras de Chiò e de Vandermonde para calcular determinantes de matrizes. 2) A regra de Chiò permite calcular determinantes de ordem maior que 4 reduzindo a ordem de 1. 3) Matrizes de Vandermonde são aquelas cujas linhas são potências de uma mesma base, e seu determinante pode ser calculado de forma direta.

1. DETERMINANTES Regra de Chiò Matriz de Vandermonde Cálculo de Matriz Inversa por meio de Determinantes

2. Relembrando o que já sabemos... Já vimos que podemos calcular o determinante de qualquer matriz de ordem n > 1 utilizando o Teorema de Laplace, mas percebemos que para facilitar nossos cálculos precisamos obter uma fila com o maior número de elementos nulos e para conseguirmos uma fila desse tipo utilizamos o Teorema de Jacobi.

3. Contudo, o que podemos observar se a matriz em questão for de ordem n > 4 ? Como por exemplo: Calcule o determinante da matriz D: D = 2 4 6 7 8 0 0 0 1 0 9 1 5 7 4 2 8 6 3 1 0 7 9 0 6

4. Abaixamento da ordem de um determinante: REGRA DE CHIÒ 1º) Deve-se ter a 11 = 1 ; suprimi-se a 1ª linha e a 1ª coluna. 2º) De cada elemento restante em A, subtraímos o produto daqueles elementos que se encontram nas “extremidades das perpendiculares” traçadas, do elemento considerado, sobre a 1ª linha e sobre a 1ª coluna. Exemplo:

5. Se na matriz A não existir elemento igual a 1 ?

6. Obs. 1: Se na matriz A, a 11 é diferente de 1, e se existir algum elemento igual a 1, podemos através de trocas de filas transformar A em uma outra matriz A” para a qual a” 11 =1. -

7. Obs.2: Se na matriz A não existir elemento igual a 1, usando o Teorema de JACOBI podemos obter a matriz onde a” 11 =1.

8. Também podemos: Obs.: P6) multiplicando-se (ou dividindo-se) os elementos de uma fila por um número, o determinante fica multiplicado (ou dividido) por esse número. R = R = 2 . det (R)  R/2 = det (R)

9. Matriz de Vandermonde (ou das potências) Chamamos matriz de Vandermonde, ou das potências, toda matriz de ordem n ≥ 2, do tipo: Isto é, as filas de M são formadas por potências de mesma base, com expoente inteiro, variando de 0 até n – 1. Obs.: 1) Os elementos da 2ª linha são chamados elementos característicos da matriz. 2) Indicamos o det. de uma matriz de Vandermonde por V ( 2, 1, -3, 5). = 8 . 4 . 3 . (-4) . (-5) . (-1) = -1920 2 1 -3 5 ? 1 1 1 1 -3 5 1 9 25 8 1 -27 125

10. Calcule o determinante:

11. Cálculo da Matriz Inversa por meio de Determinantes Antes precisamos saber: 1) Matriz dos cofatores – Seja A uma matriz quadrada de ordem n. Chamamos de matriz dos cofatores de A, e indicamos por A’, a matriz que se obtém de A, substituindo cada elemento de A por seu cofator.

12. 2) Matriz adjunta – Seja A uma matriz quadrada de ordem n e A’ a matriz dos cofatores de A. Chamamos de matriz adjunta de A, e indicamos por A , a transposta da matriz A’, isto é, A = ( A’ ) t

13. Relação para o Cálculo da inversa de uma matriz quadrada K Se K é uma matriz quadrada de ordem n e det ( K ) ≠ 0, então a inversa de K é: K -1 = 1 . K det (K) Teorema : K . K = K . K = det (K) . I n