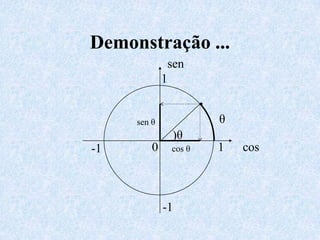
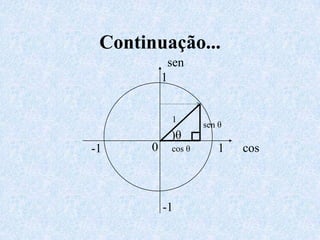
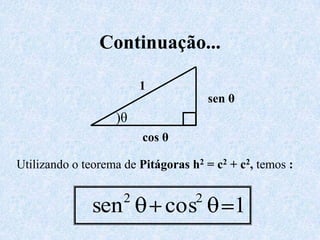
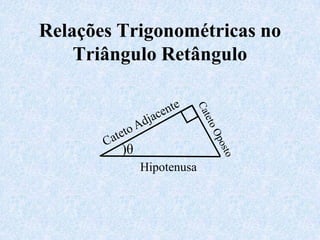
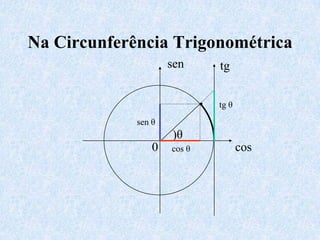
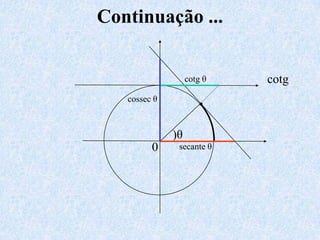
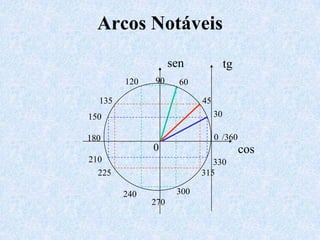
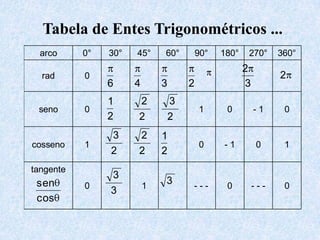
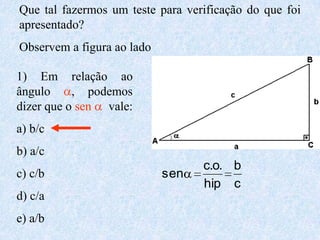
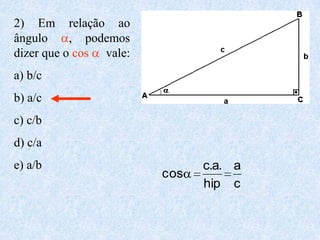
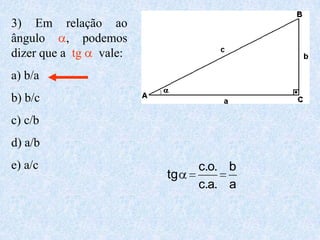
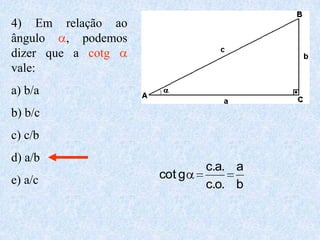
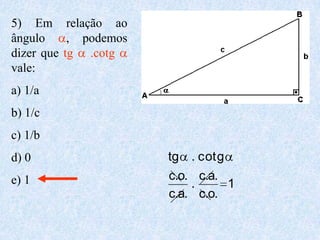
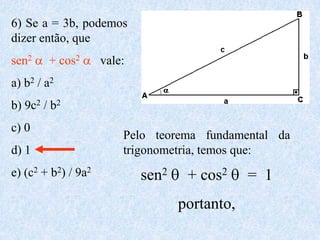
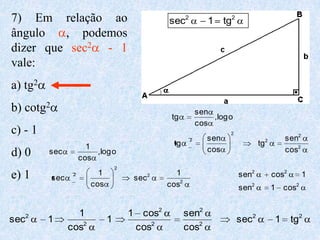
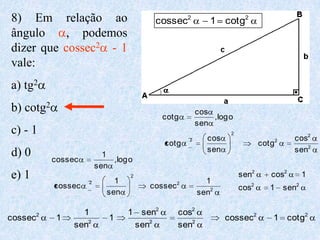
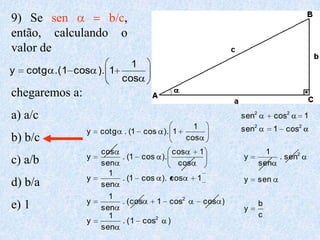
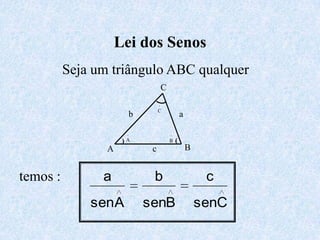
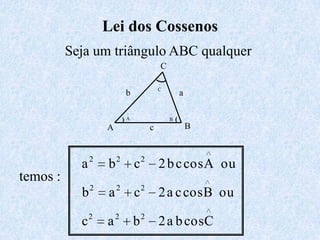
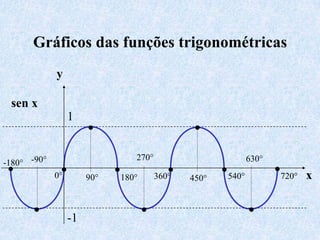
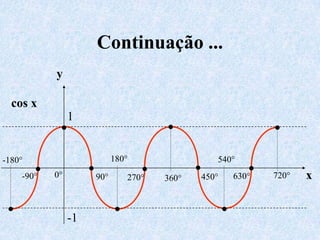
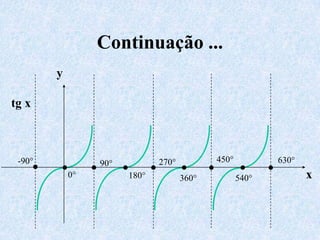
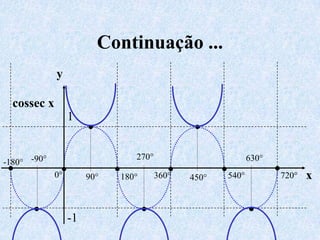
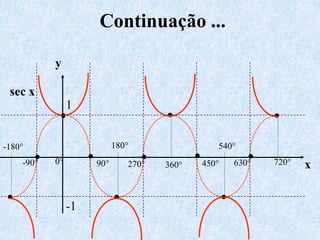
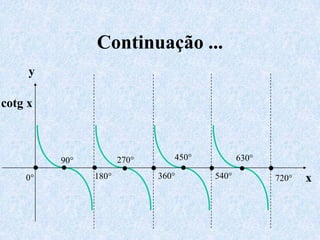
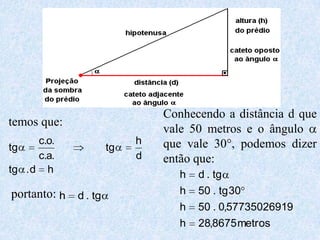
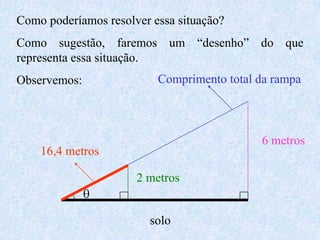
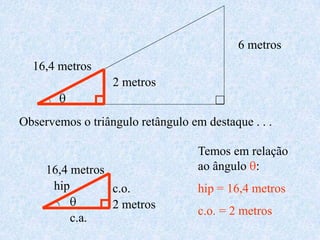
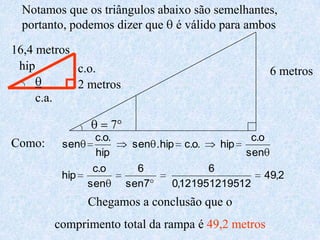
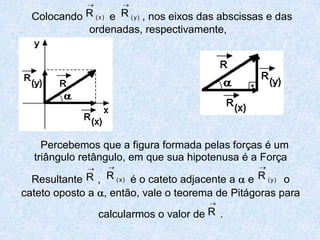
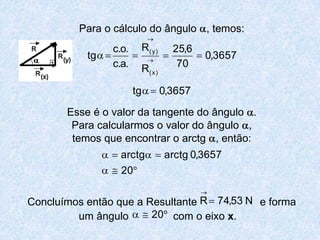
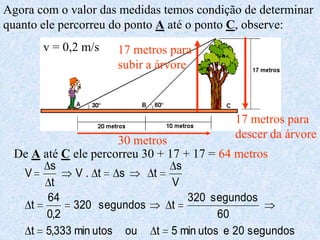
O documento apresenta os conceitos fundamentais da trigonometria, incluindo o teorema fundamental da trigonometria, relações trigonométricas no triângulo retângulo, gráficos das funções trigonométricas e aplicações em problemas geométricos e de mecânica.

1. Teorema Fundamental da Trigonometria

2. Demonstração ... sen 1 sen θ1 cos0-1cos θ-1·θ)θ

3. Continuação... sen 1 1sen θ)θ01 cos-1cos θ-1

4. Continuação...1sen θ)θcos θUtilizando o teorema de Pitágorash2 = c2 + c2, temos :

5. Relações Trigonométricas no Triângulo Retângulo)θCateto AdjacenteCateto OpostoHipotenusa

6. Continuação ...Relação no Triângulo RetânguloEnte TrigonométricoSeno de θCosseno de θTangente de θCossecante de θSecante de θCotangente de θ

7. Na Circunferência Trigonométricatg θsen θcos θ sen tg ·)θ cos0

8. Continuação ...cotg cotg θcossec θsecante θ·)θ0

9. sen tg90°120°135°150°0°/360°180°0cos210°330°225°315°300°240°270°Arcos Notáveis60°45°30°

10. Tabela de Entes Trigonométricos ...

11. Vamos pensar . . .

12. Que tal fazermos um teste para verificação do que foi apresentado?Observem a figura ao lado1) Em relação ao ângulo a, podemos dizer que o sen a vale:a) b/cb) a/cc) c/bd) c/ae) a/b

13. 2) Em relação ao ângulo a, podemos dizer que o cos a vale:a) b/cb) a/cc) c/bd) c/ae) a/b

14. 3) Em relação ao ângulo a, podemos dizer que a tg a vale:a) b/ab) b/cc) c/bd) a/be) a/c

15. 4) Em relação ao ângulo a, podemos dizer que a cotg a vale:a) b/ab) b/cc) c/bd) a/be) a/c

16. 5) Em relação ao ângulo a, podemos dizer que tg a .cotg a vale:a) 1/ab) 1/cc) 1/bd) 0e) 1

17. 6) Se a = 3b, podemos dizer então, que sen2a + cos2avale:a) b2 / a2b) 9c2 / b2c) 0d) 1e) (c2 + b2) / 9a2Pelo teorema fundamental da trigonometria, temos que:sen2q + cos2q = 1portanto,

18. 7) Em relação ao ângulo a, podemos dizer que sec2a - 1 vale:a) tg2ab) cotg2ac) - 1d) 0e) 1

19. 8) Em relação ao ângulo a, podemos dizer que cossec2a - 1 vale:a) tg2ab) cotg2ac) - 1d) 0e) 1

20. 9) Se sen a = b/c, então, calculando o valor de chegaremos a:a) a/c b) b/c c) a/bd) b/ae) 1

21. Voltando a parte teórica

22. Lei dos SenosCab ()BAcSeja um triângulo ABC qualquertemos :

23. Cabc ()BALei dos CossenosSeja um triângulo ABC qualquertemos :

24. Continuação ...Curiosidade : Quando um dos ângulos do triângulo é reto, por exemplo, Â= 90°, temos :Sabe-se que cos 90° = 0, logo ...Temos, portanto ...Teorema de Pitágoras

25. Gráficos das funções trigonométricasy1 • • 270°630°-90°-180° • • • • • • x0°540°720°360°180°90°450° • • • -1senx

26. Continuação ...y1 • • • 180°540°-180° • • • • • x0°720°630°-90°450°90°270°360° • • • -1cosx

27. Continuação ...y450°630°-90° • • • • • • • • • 270°90°x0°180°360°540°tg x

28. Continuação ...ycossecx1270°630°-90°-180° • x0°540°720°360°180°90°450°-1 • • • • • • • • • •

29. Continuação ...ysecx1 • • • 180°540°-180°x • • • • • 0°720°630°-90°450°90°270°360° • • • -1

30. Continuação ...ycotg x450°630°270°90° • • • • • • • • • x360°540°180°0°720°

31. TRIGONOMETRIA APLICADA• Modelo matemático que indica ao número de horas do dia, com luz solar, de uma determinada cidade norte americana,“t” dias após 1º de janeiro.Fonte : J.Stewart – Cálculo vol. I – Pág. 34

32. Trigonometria Algumas Aplicações

33. Parte PráticaO exemplo clássico da Sombra Para que possamos medir (aproximadamente) a altura de um prédio, sem a necessidade de subir ao terraço, ou utilizar equipamentos sofisticados, seria necessário somente 2 elementos. São eles: uma distância um ângulo Observe a seguir . . .

34. Conhecendo a distância d que vale 50 metros e o ângulo a que vale 30°, podemos dizer então que:temos que:portanto:

35. Exemplo 1A inclinação de uma rampa

36. Uma rampa com inclinação constante, (como a que existe em Brasília) tem 6 metros de altura na sua parte mais elevada. Um engenheiro começou a subir, e nota que após ter caminhado 16,4 metros sobre a rampa está a 2,0 metros de altura em relação ao solo. Será que este engenheiro somente com esses dados e uma calculadora científica conseguiria determinar o comprimento total dessa rampa e sua inclinação em relação ao solo?

37. Como poderíamos resolver essa situação?Como sugestão, faremos um “desenho” do que representa essa situação.Observemos:Comprimento total da rampa6 metros16,4 metros2 metrosqsolo

38. Observemos o triângulo retângulo em destaque . . .Temos em relação ao ângulo q:hip = 16,4 metrosc.o. = 2 metros16,4 metroshipc.o.q2 metrosc.a.

39. Como: hip = 16,4 metrosc.o. = 2 metros16,4 metroshipc.o.q2 metrosc.a.Obs.: quando dizemos que arcsen a = 1/2 , podemos transformar essa igualdade em uma pergunta: “qual é o arco, cujo seno vale 1/2?”, a resposta seria dizer que a = 30°.

40. Em nosso exercício, chegamos a conclusão que:sen q = 0,121951219512, logo podemos encontrar o ângulo q, com o auxílio da calculadora que normalmente utiliza as funções ASIN ou SIN-1, então, devemos digitar 0,121951219512 e a opção acima de sua calculadora. Se o processo foi realizado corretamente, deverá ser encontrado o valor 7,00472640907, que iremos considerar como aproximadamente 7°. Encontramos assim, a inclinação da rampa!

41. Notamos que os triângulos abaixo são semelhantes, portanto, podemos dizer que q é válido para ambos16,4 metroshipc.o.6 metrosq2 metrosc.a.q = 7°Como:Chegamos a conclusão que o comprimento total da rampa é 49,2 metros

42. Exemplo 2Mecânica Geral ou Trigonometria?

43. Os conceitos trigonométricos aparecem com muita freqüência no estudo da Física, Topografia, Astronomia e de muitos outros assuntos.Observemos os exemplos a seguir:Em relação ao sistema de forças representado na figura, onde F1 = 20N, F2 = 100N, F3 = 40N e F4 = 10N, você seria capaz de determinar a intensidade da resultante do sistema e o ângulo que essa resultante forma com o eixo das abscissas (x)?

50. Desafio !

51. Um alpinista muito ágil, percorre um trajeto passando pelos pontos A e B. Não se sabe ao certo o que ocorreu, mas ele conseguiu com o material apropriado chegar a conclusão das medidas abaixo mencionadas. Quando chega até a árvore ele percebe que o único caminho que o levará até o ponto C é escalando-a. (a altura da árvore é representada por h - despreze a largura do tronco) Se sua velocidade média é de 0,2 m/s, quantos minutos ele demorou para sair do ponto A e chegar ao ponto C? ( )

52. Solução:Resumidamente, temos o triângulo ao lado que representa nosso desafio.

53. Igualando o h das equações ( I ) e (II)Como

54. Agora com o valor das medidas temos condição de determinar quanto ele percorreu do ponto A até o ponto C, observe:v = 0,2 m/s17 metros para subir a árvore17 metros para descer da árvore30 metrosDe A até C ele percorreu 30 + 17 + 17 = 64 metros

55. Obrigado pela participação de todos!!!Prof. LucianoRibeiro