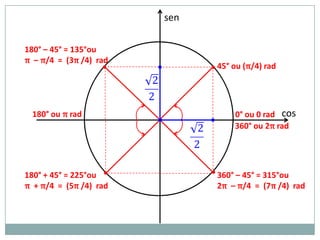
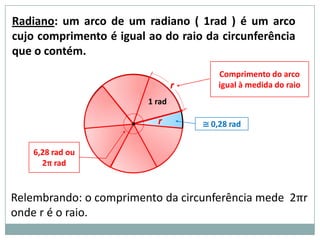
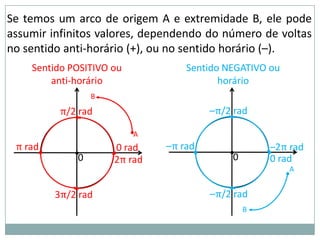
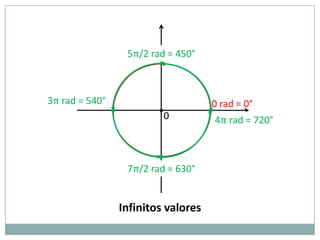
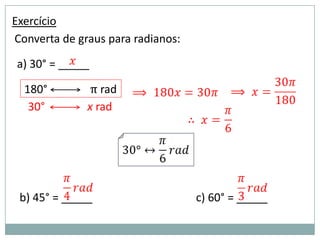
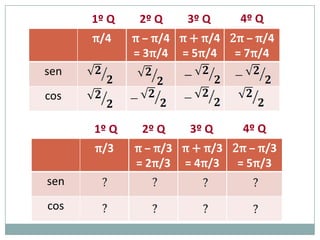
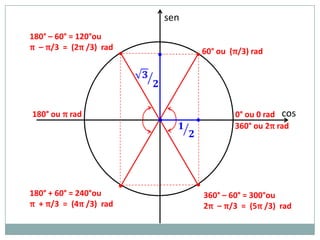
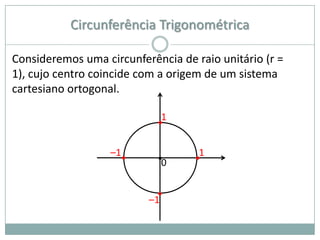
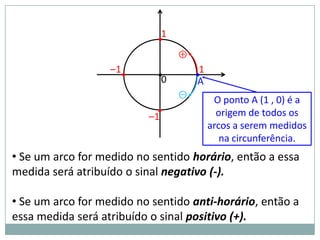
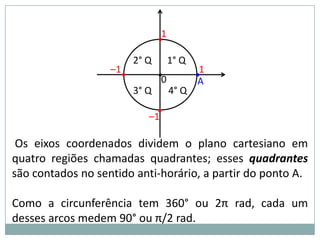
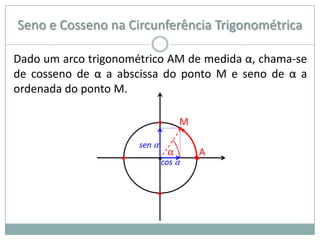
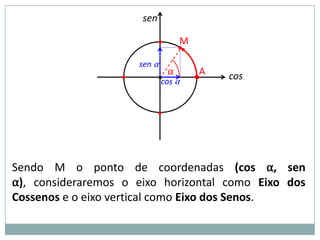
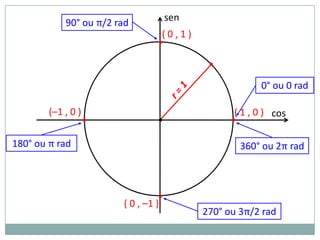
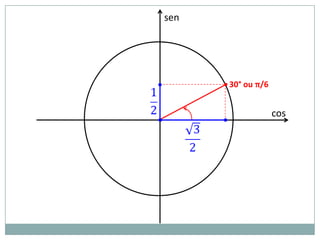
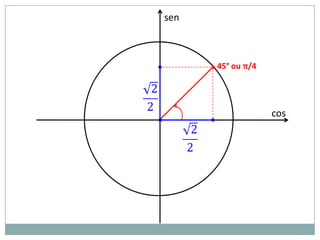
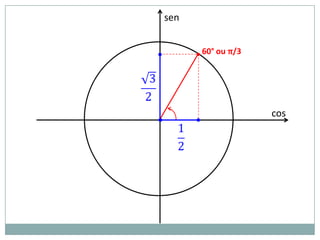
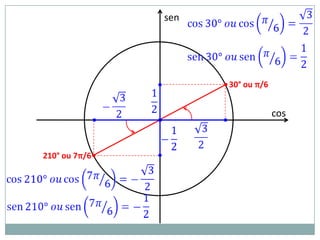
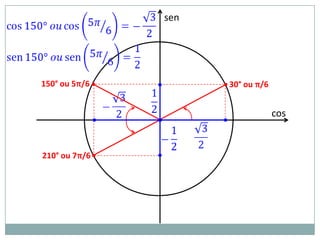
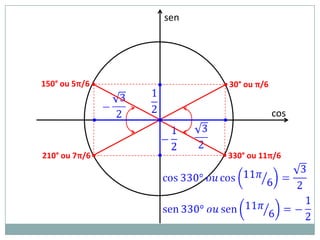
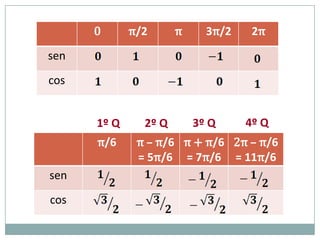
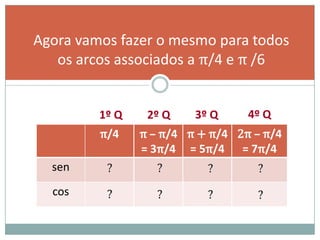
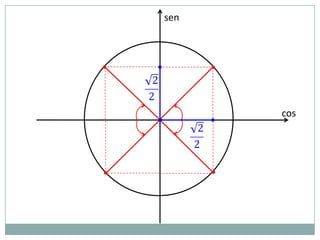
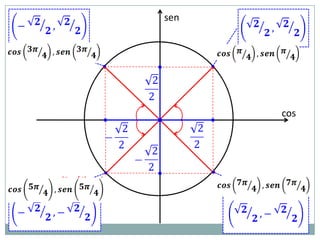
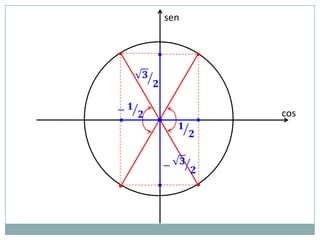
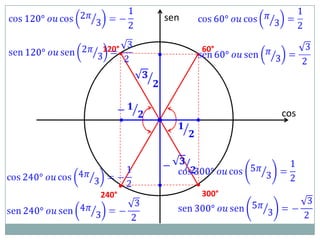
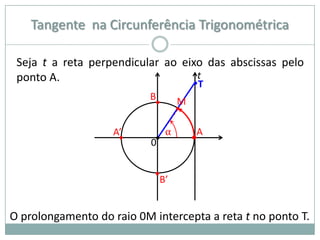
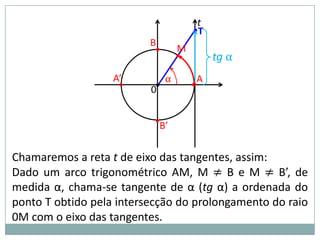
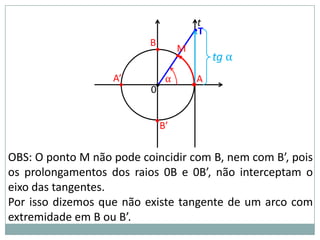
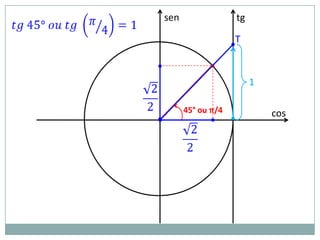
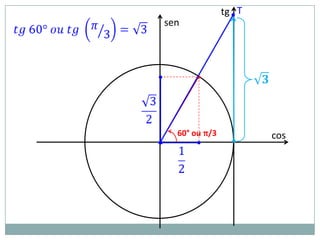
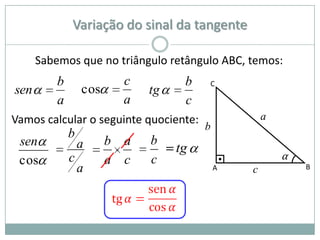
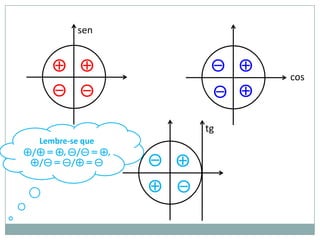
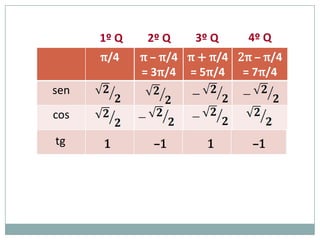
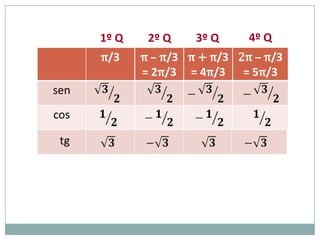
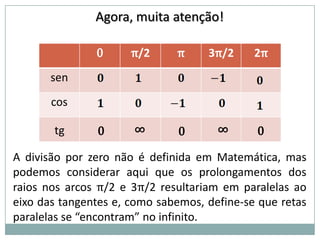
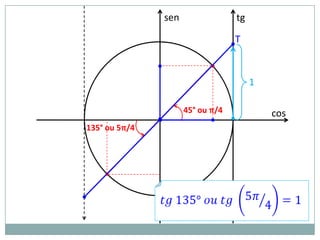
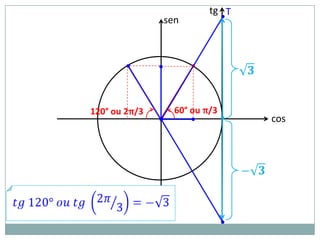
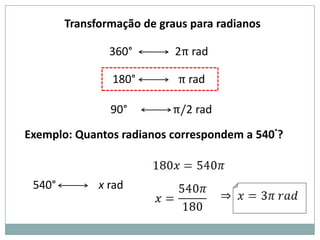
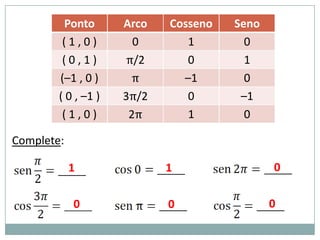
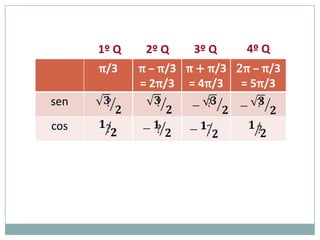
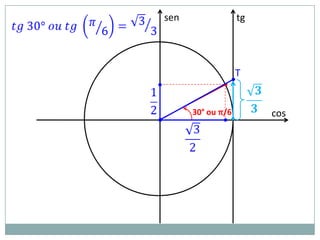
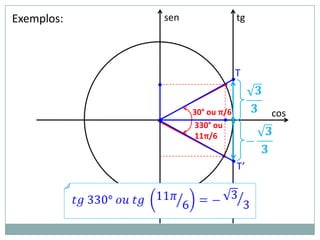
O documento apresenta os conceitos fundamentais do ciclo trigonométrico, incluindo: 1) As unidades grau e radiano para medidas de arcos; 2) A circunferência trigonométrica e a definição de seno, cosseno e tangente de um ângulo; 3) Exemplos numéricos de conversão entre graus e radianos e cálculos de seno, cosseno e tangente.

1. CICLO TRIGONOMÉTRICO
P R O F E S S O R A T E L M A C A S T R O S I LV A

2. Medidas de Arcos
As unidades mais usadas são o grau (°) e o radiano (rad).
Grau: é quando dividimos uma circunferência em 360
partes congruentes, sendo cada uma dessas partes
correspondentes a um arco de um grau (1o).

3. Radiano: um arco de um radiano ( 1rad ) é um arco
cujo comprimento é igual ao do raio da circunferência
que o contém.
Comprimento do arco
r igual à medida do raio
1 rad
•
• r ≅ 0,28 rad
6,28 rad ou
2π rad
Relembrando: o comprimento da circunferência mede 2πr
onde r é o raio.

4. Transformação de graus para radianos
360° 2π rad
180° π rad
90° π/2 rad
Exemplo: Quantos radianos correspondem a 540°?
540° x rad

5. Circunferência Trigonométrica
Consideremos uma circunferência de raio unitário (r =
1), cujo centro coincide com a origem de um sistema
cartesiano ortogonal.
1
•
–1•
•0 •1
•
–1

6. 1
•
⊕
–1•
•0 •1
A
⊖
O ponto A (1 , 0) é a
• origem de todos os
–1
arcos a serem medidos
na circunferência.
• Se um arco for medido no sentido horário, então a essa
medida será atribuído o sinal negativo (-).
• Se um arco for medido no sentido anti-horário, então a
essa medida será atribuído o sinal positivo (+).

7. 1
•
2° Q 1° Q
–1•
•0 •1
A
3° Q 4° Q
•
–1
Os eixos coordenados dividem o plano cartesiano em
quatro regiões chamadas quadrantes; esses quadrantes
são contados no sentido anti-horário, a partir do ponto A.
Como a circunferência tem 360° ou 2π rad, cada um
desses arcos medem 90° ou π/2 rad.

8. Se temos um arco de origem A e extremidade B, ele pode
assumir infinitos valores, dependendo do número de voltas
no sentido anti-horário (+), ou no sentido horário (–).
Sentido POSITIVO ou Sentido NEGATIVO ou
anti-horário horário
B
π/2 rad –π/2 rad
• •
A
π rad –π rad
• •0 •0 rad • •0 •–2π rad
2π rad 0 rad
A
• •
3π/2 rad –π/2 rad
B

9. 5π/2 rad = 450°
π/2 rad = 90°
•
3ππ rad =540°
rad = 180° 0 rad = 0°
• • •
0 2π rad = 360°
4π rad = 720°
•
3π/2 rad ==270°
7π/2 rad 630°
Infinitos valores

10. Seno e Cosseno na Circunferência Trigonométrica
Dado um arco trigonométrico AM de medida α, chama-se
de cosseno de α a abscissa do ponto M e seno de α a
ordenada do ponto M.
• M
•
sen α
α A
• •cos α •
•

11. sen
• M
•
sen α
α A
• •cos α • cos
•
Sendo M o ponto de coordenadas (cos α, sen
α), consideraremos o eixo horizontal como Eixo dos
Cossenos e o eixo vertical como Eixo dos Senos.

12. 90° ou π/2 rad sen
(0,1)
•
•
0° ou 0 rad
(–1 , 0 ) ( 1 , 0 ) cos
• • •
180° ou π rad 360° ou 2π rad
•
( 0 , –1 )
270° ou 3π/2 rad

13. Ponto Arco Cosseno Seno
(1,0) 0 1 0
(0,1) π/2 0 1
(–1 , 0 ) π –1 0
( 0 , –1 ) 3π/2 0 –1
(1,0) 2π 1 0
Complete:
1 1 0
0 0 0

14. Exercício
Converta de graus para radianos:
a) 30° = _____
180° π rad
30° x rad
b) 45° = _____ c) 60° = _____

15. sen
• 30° ou π/6
cos
•

16. sen
• 45° ou π/4
cos
•

17. sen
• 60° ou π/3
cos
•

18. sen
• 30° ou π/6
cos
•
210° ou 7π/6•

19. sen
150° ou 5π/6 • • 30° ou π/6
cos
•
210° ou 7π/6 •

20. sen
150° ou 5π/6 • • 30° ou π/6
cos
•
210° ou 7π/6 • • 330° ou 11π/6

21. 0 π/2 π 3π/2 2π
sen
cos
1º Q 2º Q 3º Q 4º Q
π/6 π – π/6 π + π/6 2π – π/6
= 5π/6 = 7π/6 = 11π/6
sen
cos

22. Agora vamos fazer o mesmo para todos
os arcos associados a π/4 e π /6
1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos

23. sen
180° – 45° = 135°ou
π – π/4 = (3π /4) rad
• • 45° ou (π/4) rad
180° ou π rad 0° ou 0 rad cos
•
360° ou 2π rad
• •
180° + 45° = 225°ou 360° – 45° = 315°ou
π + π/4 = (5π /4) rad 2π – π/4 = (7π /4) rad

24. sen
• •
cos
•
• •

25. sen
(3π /4) rad (π/4) rad
• •
cos
•
• •
(5π /4) rad (7π /4) rad

26. 1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos
1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos

27. sen
180° – 60° = 120°ou
π – π/3 = (2π /3) rad
• • 60° ou (π/3) rad
180° ou π rad 0° ou 0 rad cos
•
360° ou 2π rad
• •
180° + 60° = 240°ou 360° – 60° = 300°ou
π + π/3 = (4π /3) rad 2π – π/3 = (5π /3) rad

28. sen
• •
cos
•
• •

29. sen
120° 60°
• •
cos
•
• •
240° 300°

30. 1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos

31. Tangente na Circunferência Trigonométrica
Seja t a reta perpendicular ao eixo das abscissas pelo
ponto A. t
• T
B
• M
•
A’ α A
• 0• •
•
B’
O prolongamento do raio 0M intercepta a reta t no ponto T.

32. t
•T
B
• M
• tg α
A’ α A
• 0• •
•B’
Chamaremos a reta t de eixo das tangentes, assim:
Dado um arco trigonométrico AM, M ≠ B e M ≠ B’, de
medida α, chama-se tangente de α (tg α) a ordenada do
ponto T obtido pela intersecção do prolongamento do raio
0M com o eixo das tangentes.

33. t
•T
B
• M
• tg α
A’ α A
• 0• •
•B’
OBS: O ponto M não pode coincidir com B, nem com B’, pois
os prolongamentos dos raios 0B e 0B’, não interceptam o
eixo das tangentes.
Por isso dizemos que não existe tangente de um arco com
extremidade em B ou B’.

34. Tabela das principais razões trigonométricas
30º ou 45º ou 60º ou
(π/6) rad (π/4) rad (π/3) rad
1 2 3
sen
2 2 2
3 2 1
cos
2 2 2
3 1
tg 3
3

35. sen tg
T
•
30° ou π/6 cos
•

36. sen tg
T
•
1
45° ou π/4 cos
•

37. tg T
sen
•
60° ou π/3 cos
•

38. Variação do sinal da tangente
Sabemos que no triângulo retângulo ABC, temos:
b c b C
sen cos tg
a a c
Vamos calcular o seguinte quociente: a
b
b
sen a b a b
tg
cos c a c c α
a A c B

39. sen
⊕ ⊕ ⊖ ⊕
cos
⊖ ⊖ ⊖ ⊕
tg
Lembre-se que
⊕/⊕ = ⊕, ⊖/⊖ = ⊕,
⊕/⊖ = ⊖/⊕ = ⊖ ⊖ ⊕
⊕ ⊖

40. 1º Q 2º Q 3º Q 4º Q
π/6 π – π/6 π + π/6 2π – π/6
= 5π/6 = 7π/6 = 11π/6
sen
cos
tg

41. 1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos
tg 1 –1 1 –1

42. 1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos
tg

43. Agora, muita atenção!
0 π/2 π 3π/2 2π
sen
cos
tg 0 ∞ 0 ∞ 0
A divisão por zero não é definida em Matemática, mas
podemos considerar aqui que os prolongamentos dos
raios nos arcos π/2 e 3π/2 resultariam em paralelas ao
eixo das tangentes e, como sabemos, define-se que retas
paralelas se “encontram” no infinito.

44. Exemplos: sen tg
T
•
30° ou π/6 cos
• 330° ou
11π/6
•
T’

45. sen tg
T
•
1
45° ou π/4 cos
•
135° ou 5π/4
•

46. tg T
sen
• •
120° ou 2π/3 60° ou π/3
• cos

47. ISERJ – 2011
Fonte: Trabalho da Professora Gertrudes , PUC-RS