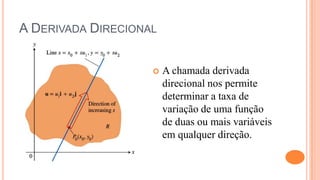
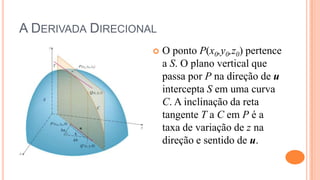
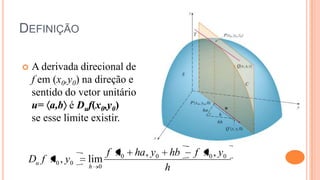
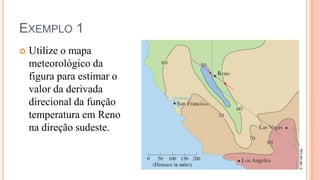
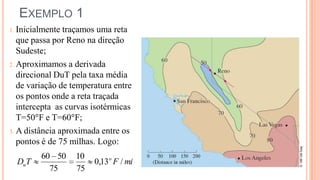
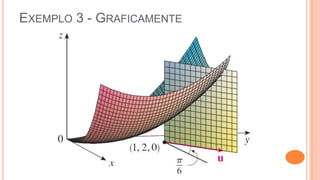
O documento discute derivadas direcionais, que fornecem a taxa de variação de uma função de várias variáveis em qualquer direção. A derivada direcional é definida como o limite da taxa de variação da função ao longo de uma reta na direção de um vetor unitário. Ela pode ser calculada como a combinação linear das derivadas parciais com os componentes do vetor unitário. Exemplos ilustram o cálculo da derivada direcional em diferentes situações.

1. Faculdade de Ciência e Tecnologia de Montes Claros
Disciplina: Cálculo III – Profª Sara Morais
Engenharia de Controle e Automação
DERIVADAS DIRECIONAIS
Acadêmicos:
Amanda Ramos, Ana Laissa, Elcimar, Érika e Warley

2. INTRODUÇÃO
 As derivadas parciais nos fornecem as taxas de variação de uma
função em direções paralelas aos eixos coordenados x, y e/ou z.
 Utilizando a regra da cadeia, suponha que z=f(x,y) seja uma
função diferenciável de x e y, onde x=g(t) e y=h(t) são funções
diferenciáveis de t. Então:
dz f x f y
dt x t y t
 Podemos calcular a taxa de variação em relação a uma
direção qualquer?

3. A DERIVADA DIRECIONAL
 A chamada derivada
direcional nos permite
determinar a taxa de
variação de uma função
de duas ou mais variáveis
em qualquer direção.

4. A DERIVADA DIRECIONAL
 Suponha que queiramos
determinar a taxa de
variação de z no ponto
(x0,y0) na direção e sentido
de um vetor unitário
arbitrário u= a,b .
Devemos considerar a
superfície S com equação
z=f(x,y) e tomar z0=f(x0,y0).

5. A DERIVADA DIRECIONAL
 O ponto P(x0,y0,z0) pertence
a S. O plano vertical que
passa por P na direção de u
intercepta S em uma curva
C. A inclinação da reta
tangente T a C em P é a
taxa de variação de z na
direção e sentido de u.

6. DEFINIÇÃO
 A derivada direcional de
f em (x0,y0) na direção e
sentido do vetor unitário
u= a,b é Duf(x0,y0)
se esse limite existir.
f x0 ha , y0 hb f x0 , y0
Du f x0 , y0 lim
h 0 h

7. TEOREMA
 Se é uma função diferenciável em x e y então f tem
derivada direcional na direção de qualquer vetor u= a,b
e
Du f x0 , y0 f x x0 , y0 a f y x0 , y0 b
 Se o versor u faz um ângulo com o eixo x positivo,
então podemos escrever u= cos ,sen e a fórmula do
Teorema fica:
Du f x0 , y0 f x x0 , y0 cos f y x0 , y0 sen

9. EXEMPLO 1
 Utilize o mapa
meteorológico da
figura para estimar o
valor da derivada
direcional da função
temperatura em Reno
na direção sudeste.

10. EXEMPLO 1
1. Inicialmente traçamos uma reta
que passa por Reno na direção
Sudeste;
2. Aproximamos a derivada
direcional DuT pela taxa média
de variação de temperatura entre
os pontos onde a reta traçada
intercepta as curvas isotérmicas
T=50 F e T=60 F;
3. A distância aproximada entre os
pontos é de 75 milhas. Logo:
60 50 10
DuT 0,13o F / mi
75 75

11. EXEMPLO 2
 Encontre a derivada de f(x,y)=x2+xy em P0(1,2) na
direção do versor u.
1 1
u i j
2 2
Solução:
1 1 1 1 5
Du f 2x y x 21 2 1
2 2 2 2 2

12. EXEMPLO 3
 Determine a derivada direcional Duf(x,y) se
f(x,y)=x3-3xy+4y2 e u é o vetor unitário dado pelo ângulo
= /6. Qual será Duf(1,2)?
1
Du f x, y 3 3x 2 3x 8 3 3 y
2
13 3 3
Du f 1,2 3,901
2

13. EXEMPLO 3 - GRAFICAMENTE

14. OBRIGADO!
Fontes:
THOMAS, George. Cálculo 2
STEWART, James. Cálculo 2