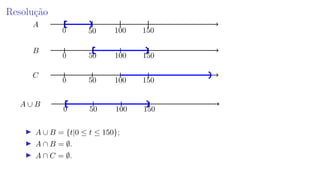
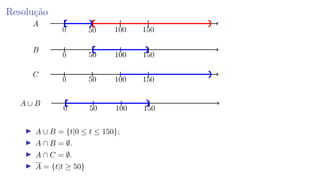
A aula introduz conceitos básicos de probabilidade como experimentos aleatórios, espaço amostral, eventos e operações entre conjuntos. É resolvida uma questão sobre eventos relacionados ao tempo para realização de uma tarefa por um marinheiro, onde a alternativa correta é que o evento A é igual a {t|t ≥ 50}.

1. Concurseiro Estatístico
Anselmo Alves de Sousa
Estatístico - CONRE 9743
+5521980721945
concurseiro_estatistico@outlook.com

2. Aula 1 Introdução à Probabilidade
Experimentos Aleatórios;
Espaço amostral Ω;
Eventos;
Notações e Operações entre Conjuntos;
Resolução de questão: CAP Marinha.

3. Experimento Aleatório
Na natureza, muitas situações que envolvem incertezas. Elas são
denominadas de fenômenos ou experimentos aleatórios.
Qual a chance do Ceará ser rebaixado para a série B do campeonato brasileiro?

4. Experimento Aleatório
Na natureza, muitas situações que envolvem incertezas. Elas são
denominadas de fenômenos ou experimentos aleatórios.
Uma lâmpada é fabricada. Em seguida é colocada em um soquete e anota-se o
tempo decorrido (em horas) até queimar.

5. Experimento Aleatório
Na natureza, muitas situações que envolvem incertezas. Elas são
denominadas de fenômenos ou experimentos aleatórios.
Em uma linha de produção, fabrica-se peças em série. Conta-se o número de
peças defeituosas produzidas em um período de 24h.

6. Experimento Aleatório
Na natureza, muitas situações que envolvem incertezas. Elas são
denominadas de fenômenos ou experimentos aleatórios.
Uma moeda é jogada 4 vezes e anota-se o número de caras obtido;

7. Experimento Aleatório
Características dos fenômenos ou experimentos aleatórios.
(Para uma certa abordagem probabilística)
um experimento poderá ser repetido indenidamente, sob condições inalteradas;
Não somos capazes de armar que resultado ocorrerá, mas podemos desccever o
conjunto de todos os resultados possíveis;
Quando o experimento for realizado repetidas vezes, os resultados mostrarão
certa regularidade (um número grande de vezes).

8. Espaço Amostral
Para cada experimento aleatório, denimos o espaço amostral como o
conjunto de todos os resultados possíveis.
Tempo de vida da lâmpada:
Ω = {t ∈ R : t ≥ 0}
Número de peças defeituosas:
Ω = {0, 1, 2, . . . , N}
N é o número máximo que se pode produzir em 24h.
Moeda jogada 4 vezes (# caras):
Ω = {0, 1, 2, 3, 4}

9. Eventos
Uma noção fundamental em probabilidade é o conceito de evento.
Um evento A, associado a um particular espaço amostral, Ω , associado a um
experimento aleatório, é um subconjunto de Ω;
Admitimos que o próprio Ω é um evento. É o chamado evento certo.
Dizemos que ∅ é o evento impossível (de ocorrer).
Exemplos:
A = {t ∈ R : t 3} ⇒ lâmpada queima em menos de 3 h;
B = {0} ⇒ todas as peças sem defeito;
C = {2} ⇒ duas caras ocorrem.

10. Eventos
Um espaço amostral nito ou innito enumerável é tal que qualquer de
seus subconjuntos pode ser considerado um evento;
Exemplo:
Ω = {ω1, ω2, . . . , ωn, . . .}
Os elementos de Ω são pontos amostrais ou eventos elementares:
A = {ω1}, B = {ω2}, C = {ω3} . . .
Essa notação é praticamente útil para entendermos algumas abordagens
em probabilidade.
A medida que avançarmos introduziremos novas notações úteis.

11. Notações e Operações entre Conjuntos
Sejam A e B eventos e A1, A2, . . . , An uma coleção nita de eventos.
A ∪ B é o evento que ocorrerá se, e somente se, A ou B (ou ambos) ocorrerem;
A ∩ B é o evento que ocorrerá se, e somente se, A e B ocorrerem;
A ou Ac
é o evento que ocorrerá se, e somente se, não ocorrer A;
n
i=1
Ai é o evento que ocorrerá se, e somente se, ao menos um dos Ai ocorrer;
n
i=1
Ai é o evento que ocorrerá se, e somente se, todos os Ai ocorrer;

12. Aula 1 Introdução à Probabilidade
Experimentos Aleatórios;
Espaço amostral Ω;
Eventos;
Notações e Operações entre Conjuntos;
Resolução de questão: CAP Marinha.

13. MARINHA CAP Técnico em Estatística
34. Considere que, num experimento, uma determinada tarefa é realizada
por um marinheiro em um tempo determinado t. Admita que o espaço
amostral seja {t|t 0} e que A, B e C sejam três eventos denidos da
seguinte maneira:
A = {t|t 50}; B = {t|50 t ≤ 150}; C = {t|t 100}
Sendo assim, é correto armar que:
(A) A ∪ B = {t|50 t ≤ 150}
(B) A ∩ B = {t|t ≤ 150}
(C) A ∩ B = ∅
(D) A = {t|t ≥ 50}
(E) B ∪ C = {t|t ≥ 50}

14. Resolução
0 100 15050
A
0 100 15050
B
0 100 15050
C
0 100 15050
A ∪ B
A ∪ B = {t|0 ≤ t ≤ 150};
A ∩ B = ∅.
A ∩ C = ∅.

15. Resolução
0 100 15050
A
0 100 15050
B
0 100 15050
C
0 100 15050
A ∪ B
A ∪ B = {t|0 ≤ t ≤ 150};
A ∩ B = ∅.
A ∩ C = ∅.
A = {t|t ≥ 50}

16. MARINHA CAP Técnico em Estatística
34. Considere que, num experimento, uma determinada tarefa é realizada
por um marinheiro em um tempo determinado t. Admita que o espaço
amostrai seja {t|t 0} e que A, B e C sejam três eventos denidos da
seguinte maneira:
A = {t|t 50}; B = {t|50 t ≤ 150}; C = {t|t 100}
Sendo assim, é correto armar que:
(A) A ∪ B = {t|50 t ≤ 150}
(B) A ∩ B = {t|t ≤ 150}
(C) A ∩ B = ∅
(D) A = {t|t ≥ 50}
(E) B ∪ C = {t|t ≥ 50}

17. MARINHA CAP Técnico em Estatística
34. Considere que, num experimento, uma determinada tarefa é realizada
por um marinheiro em um tempo determinado t. Admita que o espaço
amostrai seja {t|t 0} e que A, B e C sejam três eventos denidos da
seguinte maneira:
A = {t|t 50}; B = {t|50 t ≤ 150}; C = {t|t 100}
Sendo assim, é correto armar que:
(A)
(B)
(C)
(D) A = {t|t ≥ 50}
(E)

18. Conteúdo Exclusivo
concurseiro_estatistico@outlook.com
+5521980721945
Anselmo Alves de Sousa
Estatístico - CONRE 9743