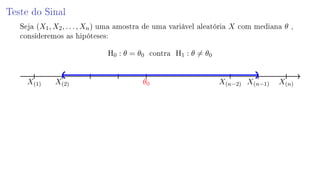
O documento descreve um teste estatístico para verificar se a mediana do teor de impureza de um produto químico é igual a 2,5 ppm. Foram observadas 36 amostras aleatórias, sendo que 24 tinham teor de impureza menor que 2,5 ppm. O teste estatístico utilizado foi o teste dos sinais, que comparou o número de amostras com teor menor ou maior que 2,5 ppm. O valor-p calculado para este teste foi 0,0228.

1. Concurseiro Estatístico
concurseiro_estatistico@outlook.com

2. Conteúdo Exclusivo
concurseiro_estatistico@outlook.com
+5521980721945
Anselmo Alves de Sousa
Estatístico - CONRE 9743

4. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm.

5. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm.

6. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As demais
apresentaram teor de impureza maior que 2, 5 ppm.

7. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As demais
apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais

8. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As demais
apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais , utilizando a aproximação pela distribuição
normal.

9. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As demais
apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais , utilizando a aproximação pela distribuição
normal. O valor-p desse teste é

10. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t = 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As demais
apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais , utilizando a aproximação pela distribuição
normal. O valor-p desse teste é
(A) 0, 0114
(B) 0, 0228
(C) 0, 0456
(D) 0, 9772

11. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ

12. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:

13. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0

14. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0
X(1) X(2) θ0 X(n−2) X(n−1) X(n)

15. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0
X(1) X(2) θ0 X(n−2) X(n−1) X(n)
Sejam as variáveis Di = Xi − θ0, i = 1, 2, . . . , n.

16. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0
X(1) X(2) θ0 X(n−2) X(n−1) X(n)
Sejam as variáveis Di = Xi − θ0, i = 1, 2, . . . , n.
Estatística de teste T = número de diferenças Di +.

17. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0
X(1) X(2) θ0 X(n−2) X(n−1) X(n)
Sejam as variáveis Di = Xi − θ0, i = 1, 2, . . . , n.
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)

18. Teste do Sinal
Seja (X1, X2, . . . , Xn) uma amostra de uma variável aleatória X com mediana θ ,
consideremos as hipóteses:
H0 : θ = θ0 contra H1 : θ = θ0
X(1) X(2) θ0 X(n−2) X(n−1) X(n)
Sejam as variáveis Di = Xi − θ0, i = 1, 2, . . . , n.
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)
A regra de rejeição no caso das hipóteses acima é: jeitaremos H0, a um nível
de signicância α, se (T ≤ t) ou (T ≥ t∗
).

19. CBTU-/2014 CONSULPLAN

20. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.

21. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)

22. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)
E(T) = np ⇒ E(T) = 0, 5n

23. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)
E(T) = np ⇒ E(T) = 0, 5n
Var(T) = np(1 − p) ⇒ Var(T) = 0, 25n

24. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)
E(T) = np ⇒ E(T) = 0, 5n
Var(T) = np(1 − p) ⇒ Var(T) = 0, 25n
Aproximação pela distribuição normal:

25. CBTU-/2014 CONSULPLAN
Estatística de teste T = número de diferenças Di +.
T ∼ Binomial(n, 1/2)
E(T) = np ⇒ E(T) = 0, 5n
Var(T) = np(1 − p) ⇒ Var(T) = 0, 25n
Aproximação pela distribuição normal:
T − 0, 5n
0, 5
√
n
∼ N(0, 1)

26. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5

27. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36

28. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒

29. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12

30. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)

31. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n

32. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n 12 − 18)

33. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n 12 − 18)
= Pr
T − 0, 5n
0, 5
√
n

34. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n 12 − 18)
= Pr
T − 0, 5n
0, 5
√
n
12 − 18
0, 5
√
36

35. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n 12 − 18)
= Pr
T − 0, 5n
0, 5
√
n
12 − 18
0, 5
√
36
= Pr(Z −2)

36. CBTU-/2014 CONSULPLAN
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36 , # observações 2, 5 igual a 24 ⇒ # sinais positivos = 12
p-valor = Pr(T 12)
= Pr(T − 0, 5n 12 − 18)
= Pr
T − 0, 5n
0, 5
√
n
12 − 18
0, 5
√
36
= Pr(Z −2) = 0, 0228

37. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:

38. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5

39. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36, # observações 2, 5 igual a 24 ⇒ # sinais negativos = 24

40. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36, # observações 2, 5 igual a 24 ⇒ # sinais negativos = 24
p-valor = Pr(T 24)

41. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36, # observações 2, 5 igual a 24 ⇒ # sinais negativos = 24
p-valor = Pr(T 24)
= Pr
T − 0, 5n
0, 5
√
n
24 − 18
0, 5
√
36

42. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36, # observações 2, 5 igual a 24 ⇒ # sinais negativos = 24
p-valor = Pr(T 24)
= Pr
T − 0, 5n
0, 5
√
n
24 − 18
0, 5
√
36
= Pr(Z 2)

43. CBTU-/2014 CONSULPLAN
Se considerarmos como estatística o número de sinais negativos:
H0 : θ = 2, 5 contra H1 : θ = 2, 5
n = 36, # observações 2, 5 igual a 24 ⇒ # sinais negativos = 24
p-valor = Pr(T 24)
= Pr
T − 0, 5n
0, 5
√
n
24 − 18
0, 5
√
36
= Pr(Z 2) = 0, 0228

44. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t= 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As
demais apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais, utilizando a aproximação pela distribuição
normal. O valor-p desse teste é
(A) 0, 0114
(B) 0, 0228
(C) 0, 0456
(D) 0, 9772

45. CBTU-/2014 CONSULPLAN
35. Deseja-se vericar se a mediana do teor de impureza de um produto químico
intermediário é igual a 2, 5 ppm. Observou-se que t= 24 das 36 amostras
aleatórias do produto tinham teor de impureza menor que 2, 5 ppm. As
demais apresentaram teor de impureza maior que 2, 5 ppm. Seja
Z0 =
t − 0, 5n
0, 5
√
n
a estatística do Teste dos Sinais, utilizando a aproximação pela distribuição
normal. O valor-p desse teste é
(A)
(B) 0, 0228
(C)
(D)

46. Conteúdo Exclusivo
concurseiro_estatistico@outlook.com
+5521980721945
Anselmo Alves de Sousa
Estatístico - CONRE 9743