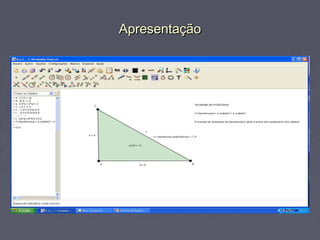
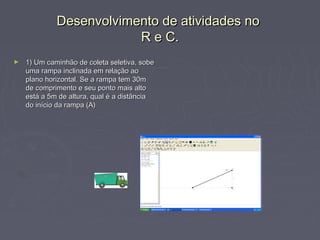
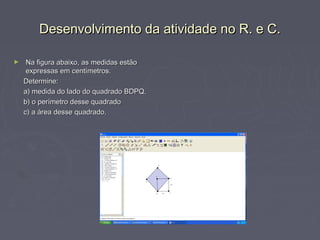
O documento apresenta um resumo de uma aula sobre o Teorema de Pitágoras, incluindo exemplos de aplicações do teorema em triângulos retângulos, quadrados e triângulos equiláteros. As etapas da atividade prática com alunos usando o software R.e C. são descritas, assim como atividades complementares propostas. Referências bibliográficas são fornecidas no final.

1. Teorema de Pitágoras
Curso de Informática Educativa I
Projeto de Execução
Aluna: Jucilene

2. Aplicações importantes do
Teorema de Pitágoras
Triângulo retângulo
Quadrado
Números irracionais

3. 1ª aula – Problema envolvendo teorema de
Pitágoras
► Observe a seguinte situação:
Rosa é arquiteta. Ao fazer a planta
de uma casa, deparou-se com a
seguinte situação: Se a altura da
escada é de 4m e o afastamento
da escada à parede é de 6m, qual
deve ser a medida do comprime-
to da escada?

4. Etapas atividade 1 – Construindo o triângulo
retângulo
1) Com a turma dividida em grupos de no máximo três aluno iniciaremos
as atividades, no laboratório de informática usando o R. e C..
Apresentando o software e os principais botões a serem utilizados na
execução da atividade.
2) Usando o botão segmento de reta traçaremos o segmento AB (cateto) e
em seguida usando a reta perpendicular da barra de ferramentas
traçamos o segmento AC (cateto), formando o ângulo de 90º e faremos
a união BC formando o triângulo retângulo.
3) Registraremos o valor do segmento AB = 6 m, em seguida AC = 4 m e
para BC = x.
4) Usando o R.e C. efetuaremos os cálculos para determinar o valor da
hipotenusa, usando o valor com aproximação de duas casas decimais.
5) Nesse momento discutiremos os valores assumido quando elevamos os
(catetos)² e efetuamos a soma determinando logo em seguida a raiz e o
valor de x que é a hipotenusa.

5. Apresentação

6. O teorema de Pitágoras no quadrado
1) Usando o papel quadriculado,
construir um quadrado ABCD
qualquer e de lado 1, em seguida
traçar a diagonal desse quadrado.
2) Em seguida mostrar aos alunos que
a diagonal do quadrado nos
apresenta dois triângulos retângulos.
3) Identificar os elementos
(cateto/hipotenusa e ângulo reto) e
em seguida usando a medida L = 1,
aplicar o teorema de Pitágoras e
apresentando o resultado como
segue:

7. O teorema de Pitágoras no triângulo equilátero
► Usando o papel quadriculado traçar o
triângulo equilátero lado = L e altura H.
Identificar os pontos do triângulo ABC,
identificar os ângulos retos.
► Comentar com os alunos sobre a
coincidência entre a altura e a medida,
pois o ponto H é ponto médio do lado
BC.
► Usando o teorema de Pitágoras
determinar a altura desse triângulo.

8. Desenvolvimento de atividades no
R e C.
► 1) Um caminhão de coleta seletiva, sobe
uma rampa inclinada em relação ao
plano horizontal. Se a rampa tem 30m
de comprimento e seu ponto mais alto
está a 5m de altura, qual é a distância
do início da rampa (A)

9. Desenvolvimento da atividade no R. e C.
► Na figura abaixo, as medidas estão
expressas em centímetros.
Determine:
a) medida do lado do quadrado BDPQ.
b) o perímetro desse quadrado
c) a área desse quadrado.

10. Atividades complementares
1) Os alunos desenvolveram exercícios em sala de aula como
complementação do assunto abordado.
2) Com a turma dividida em grupos, já na sala de aula apresentaremos o
conteúdo descrito como segue:
Considerado um dos mais importantes teoremas da matemática, o teorema
de Pitágoras foi desenvolvido por Pitágoras de Samos, filósofo grego que
viveu no século VI a.C., fundado da mística escola Pitagórica. Além de sua
aplicação para determinar medidas não conhecidas no triângulo retângulo, o
equilátero e, entre outras, a diagonal do quadrado, temas abordas em
nossa aula, foi através das aplicações do teorema que teve início o estudo
dos números irracionais.
O teorema consiste: “ A medida do quadrado da hipotenusa é igual a medida
da soma dos quadrados dos catetos”.

11. Referências bibliográficas
Disponível em < http://colegioweb.com.br/matematica >. Acessado em
27/10/2012.
Disponível em < http://mundodaeducacao.com.br/matematica >. Acessado em
27/10/2012.
Disponível em < http://rpedu.pintoricardo.com/atividades >. Acessado em
28/10/2012.