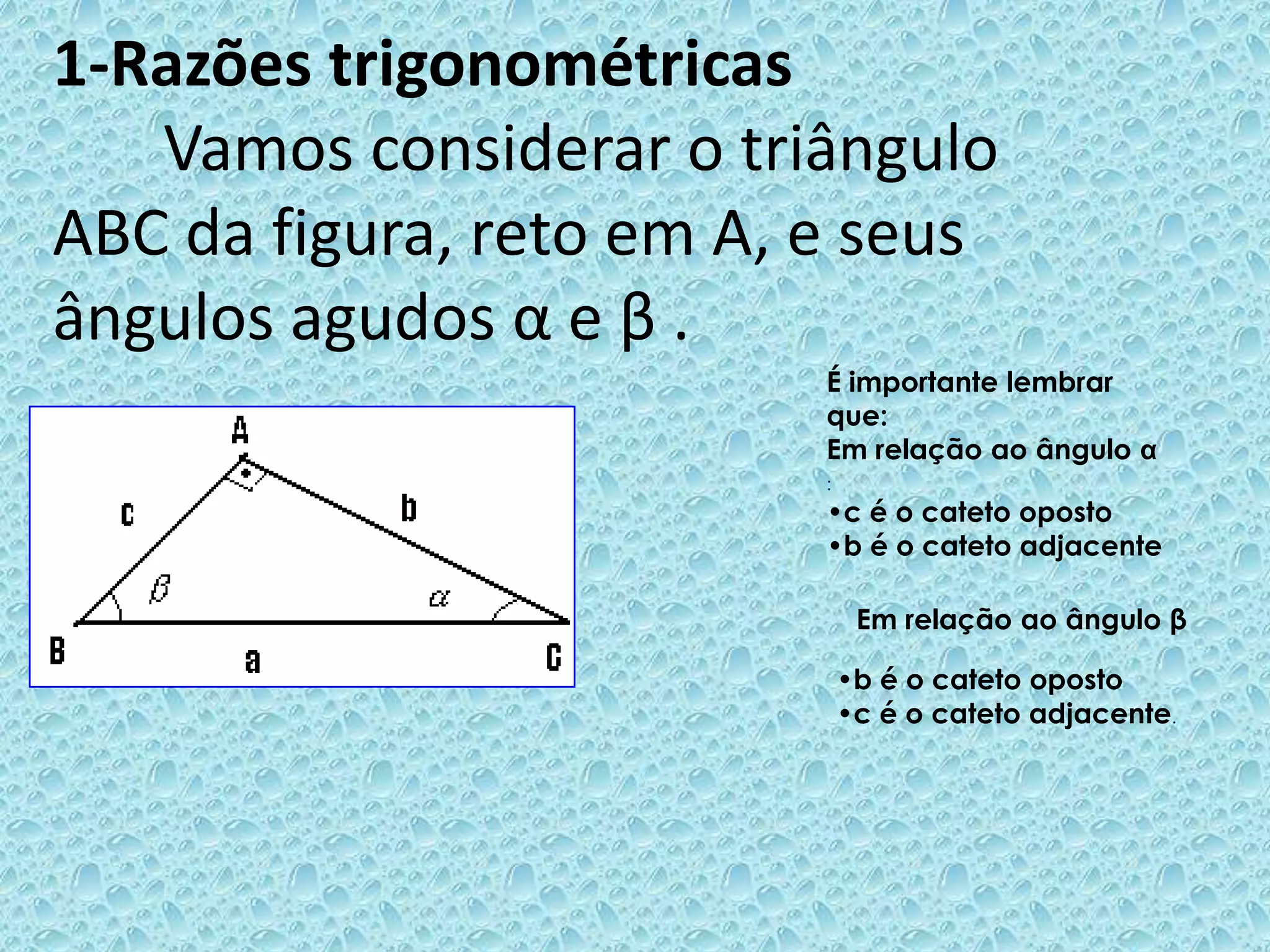
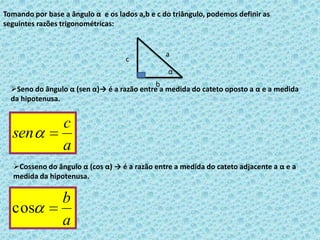
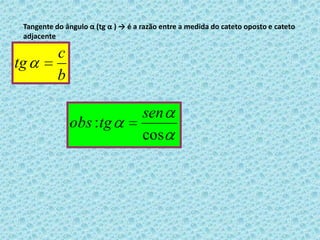
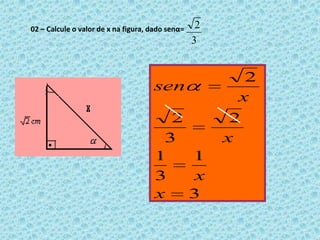
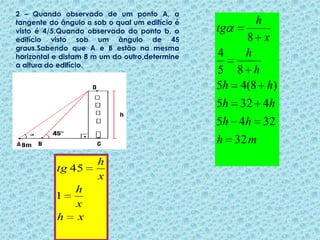
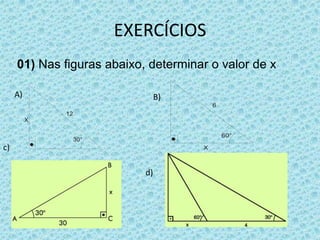
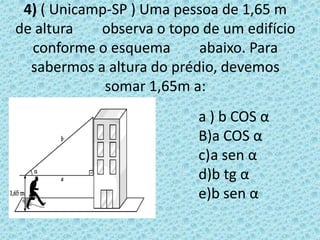
O documento discute razões trigonométricas em triângulos retângulos. Ele define seno, cosseno e tangente de um ângulo em termos das medidas dos lados do triângulo. Fornece exemplos de como calcular essas razões trigonométricas para ângulos dados e problemas envolvendo distâncias e ângulos.

1. 1-Razões trigonométricas Vamos considerar o triângulo ABC da figura, reto em A, e seus ângulos agudos α e β.É importante lembrar que:Em relação ao ângulo α:c é o cateto oposto

2. b é o cateto adjacenteEm relação ao ângulo βb é o cateto oposto

3. c é o cateto adjacente.Tomando por base a ângulo α e os lados a,b e c do triângulo, podemos definir as seguintes razões trigonométricas:acαbSeno do ângulo α (senα)-> é a razão entre a medida do cateto oposto a α e a medida da hipotenusa.

4. Cosseno do ângulo α (cosα) -> é a razão entre a medida do cateto adjacente a α e a medida da hipotenusa. Tangente do ângulo α (tgα ) -> é a razão entre a medida do cateto oposto e cateto adjacente

5. Exemplo1: Dado o triângulo retângulo, calcule senα ,cosα e tg α.

6. 02 – Calcule o valor de x na figura, dado senα=

7. 02 – Razões trigonométricas dos ângulos 30 ,45 e 60 graus.Exemplo1– uma pequena esfera é abandonada no ponto A de uma rampa. Sabendo que o ponto A está a 0,8 m do solo, calcule a distancia que a esfera deverá percorrer até chegar ao solo (ponto B).

8. 2 – Quando observado de um ponto A, a tangente do ângulo α sob o qual um edifício é visto é 4/5.Quando observado do ponto b, o edifício visto sob um ângulo de 45 graus.Sabendo que A e B estão na mesma horizontal e distam 8 m um do outro,determine a altura do edifício.

9. Relação fundamentalExiste uma outra relação importante entre seno e cosseno de um ângulo.Exemplo:Conhecendo o valor de senα= ,α ângulo agudo, determine cosα e tgα:

10. EXERCÍCIOS01) Nas figuras abaixo, determinar o valor de xA)B)c)d)

11. 02) Na cidade de Pisa, Itália, está localizada a Torre de Pisa, um dos monumentos mais famosos do mundo. Atualmente, a torre faz, na sua inclinação, um ângulo de 74º com o solo. Quando o sol está bem em cima da torre (a pino) ela projeta uma sombra de 15 m de comprimento. A que distância se encontra o ponto mais alto da torre em relação ao solo? (dados: sen 74º = 0,96 cos 74º = 0,28 tg74º = 3,4)

12. 03) ( UFSC ) Num vão entre duas paredes, deve-se construir uma rampa que vai da parte inferior de uma parede até o topo da outra. Sabendo-se que a altura das paredes é de 4 m e o vão entre elas é de 12m, determine o ângulo, em graus, que a rampa formará com o solo.