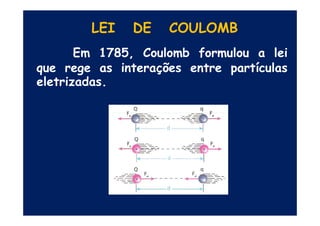
O documento discute a carga elétrica elementar e, em particular, a determinação de seu valor por Robert Millikan em 1909. Também menciona a hipótese de Murray Gell-Mann na década de 1960 sobre a existência de quarks como partículas subatômicas formadoras de prótons e nêutrons, apesar de existirem seis tipos de quarks.

1. ELETRICIDADE
Prof. Alves

2. CARGAS ELÉTRICAS
Por convenção, o próton tem carga
elétrica positiva, enquanto o elétron
possui carga negativa. O nêutron não
apresenta carga elétrica.
Legenda: nêutron
próton
elétron

3. FIQUE SABENDO !!!
Descobertas: elétron, próton e nêutron
ELÉTRON: 1897
Joseph Thomson (inglês, 1856-1940)
PRÓTONS: 1919
Ernest Rutherford (neozelandês, 1871-1937)
PRÓTONS: 1919
Ernest Rutherford (neozelandês, 1871-1937)
NÊUTRON: 1932
James Chadwick (inglês, 1891-1974)

4. CORPO NEUTRO E CORPO ELETRIZADO
± ± Corpo eletricamente neutro:
± ± ± para cada próton existe um elétron
± ±
+ ± Corpo eletrizado positivamente:
+ ± + existem mais prótons do que elétrons
+ ±+ ±
±-± Corpo eletrizado negativamente:
±-±-± apresenta mais elétrons do que prótons
±-±
ATENÇÃO !!! Um corpo neutro adquire carga positiva ao
perder elétrons. Se eletriza com carga negativa ao
receber elétrons.

5. A unidade de medida de carga elétrica no
SI é coulomb (símbolo:C), em homenagem a
Charles de Coulomb (francês, 1736-1806).
Principais submúltiplos do coulomb:
milicoulomb ( mC ), onde 1 mC = 10–3 C
microcoulomb ( µC ), onde 1 µC = 10–6 C
nanocoulomb ( nC ), onde 1 nC = 10–9 C
microcoulomb ( µC ), onde 1 µC = 10 C
nanocoulomb ( nC ), onde 1 nC = 10–9 C
Exemplos
a) 2 nC = 2.10-9 C
b) – 5 µC = - 5.10-6 C
c) 3,4 mC = 3,4.10-3 C
d) – 7,2 µC = - 7,2.10-6 C

6. CARGA DE ELÉTRICA DE UM CORPO
A quantidade de carga elétrica (Q) de um
corpo é dada por:
Q = ± N.e,
onde:
N=número de elétrons (perdidos ou ganhos)
e=carga elétrica elementar

7. FIQUE SABENDO !!!
(1) Valor da carga elétrica elementar
e = 1,6.10–19 C
(2) Carga elétrica elementar é a menor
quantidade de carga elétrica isolada existente na
natureza. Em valor absoluto (módulo) a carga do
próton e do elétron são iguais a carga elementar. Oupróton e do elétron são iguais a carga elementar. Ou
seja:
Carga do próton: + e = + 1,6.10–19 C
Carga do elétron: - e = – 1,6.10–19 C
(3) A carga elétrica de um corpo é quantizada,
isto é, ela sempre é múltiplo inteiro da carga elétrica
elementar.

8. VAMOS RESOLVER !!!
1) Uma régua de alumínio, inicialmente
neutra, perde 50 milhões de
elétrons.Determine a carga elétrica
por ela adquirida.
(Dado: e = 1,6.10–19 C)
por ela adquirida.
(Dado: e = 1,6.10–19 C)

9. Solução
Dados:
N = 50.000.000 elétrons = 5.107 elétrons
e = 1,6.10–19 C
Q = + N.eQ = + N.e
Q = + 5.107.1,6.10–19
Q = + 8.10–12 C
Resp.: Q = + 8.10–12 C

10. 2) Seja uma esfera de ferro e considere
que ela está eletricamente neutra. Caso
ela ganhe 200 bilhões de elétrons,
qual será a sua carga ?
(Dado: e = 1,6.10–19 C)(Dado: e = 1,6.10–19 C)

11. Solução
Dados:
N = 200.000.000.000 elétrons = 2.1011 elétrons
e = 1,6.10–19 C
Q = – N.eQ = – N.e
Q = – 2.1011.1,6.10–19
Q = – 3,2.10–8 C
Resp.: Q = – 3,2.10–8 C

12. 3) Mercúrio é o elemento químico de número atômico
80 e símbolo Hg. Considerando apenas prótons,
nêutrons e elétrons, responda:
(Dado: e = 1,6.10–19 C)
a) Qual a carga elétrica do núcleo do átomo de
mercúrio.
b) Qual a carga elétrica de sua eletrosfera ?
c) Qual a carga elétrica do átomo em questão.

13. Solução
Dados: Número atômico = 80 (80 prótons e 80 elétrons)
e = 1,6.10–19 C
a) Qnúcleo = + N.e
Qnúcleo = + 8.10.1,6.10–19
Qnúcleo = + 12,8.10–18 C
Qnúcleo = + 1,28.10–17 C
b) Qeletrosfera = - N.e
Qeletrosfera = - 8.10.1,6.10–19Qeletrosfera = - 8.10.1,6.10–19
Qeletrosfera = - 12,8.10–18 C
Qeletrosfera = - 1,28.10–17 C
c) A carga elétrica de um átomo é NULA ( Qátomo = zero )
Resp.: a) Qnúcleo = + 1,28.10–17 C
b) Qeletrosfera = - 1,28.10–17 C
c) Qátomo = zero

14. PRINCÍPIO DA ATRAÇÃO E REPULSÃO
Partículas com cargas elétricas de sinais iguais se
repelem, enquanto as partículas eletrizadas com cargas
de sinais opostos se atraem.

15. PROCESSOS DE ELETRIZAÇÃO
A eletrização de um corpo inicialmente
neutro pode ocorrer:
- Por atrito- Por atrito
- Por contato
- Por indução

16. • Por atrito
Corpos de materiais diferentes iniciamente
neutros ao serem atritados adquirem cargas
elétricas de mesmo módulo e sinais contrários.

17. • Por contato
Quando dois ou mais condutores são colocados
em contato, com pelo menos um deles eletrizado,
observa-se uma retribuição da carga elétrica.
ATENÇÃO!!!
Esferas condutoras idênticas (raios iguais)
ao serem contactadas adquirem cargas iguais.ao serem contactadas adquirem cargas iguais.

18. •• PorPor induçãoindução
A eletrização de um condutor neutro pode
ocorrer por uma simples aproximação de um outro
corpo eletrizado, com o aterramento do neutro. No
processo da indução eletrostática, o corpo induzido
será eletrizado sempre com carga de sinal contrário ao
da carga do indutor.

19. VAMOS RESOLVER !!!
1)Dois corpos, um de vidro e outro de
plástico, são atritados. Inicialmente ambos
estavam descarregados eletricamente, ou
seja, apresentavam-se neutros. Após o
atrito, o corpo de vidro ficou eletrizado com
uma carga de 8 milicoulombs (8 mC).uma carga de 8 milicoulombs (8 mC).
a) Qual a carga (em coulomb) adquirida pelo
corpo de plástico após o atrito ?
b) O corpo de plástico perdeu ou ganhou
elétrons? E o de vidro ?

20. Solução
O que ocorre quando corpos neutros e de materiais diferentes
são atritados é que um dos corpos transfere elétrons para o
outro.
Assim:
a) Depois do atrito, o corpo de plástico fica eletrizado com
uma carga de – 8 mC, ou seja, – 8.10-3C.
b) Como o corpo de vidro ficou eletrizado positivamenteb) Como o corpo de vidro ficou eletrizado positivamente
significa que ele perdeu elétrons para o de plástico, que adquiriu
carga negativa.
Resp.:
a) Q plástico = – 8.10-3C
b) Corpo de vidro → Perdeu elétrons
Corpo de plástico → Ganhou elétrons

21. 2) Sejam A e B corpos metálicos.O corpo A
encontra-se eletrizado, enquanto o B, neutro.
Considerando que tais corpos serão postos
em contato:
a) Qual o sinal da carga adquirida pelo
corpo B após serem contactados se o A tem
carga negativa ?
corpo B após serem contactados se o A tem
carga negativa ?
b) Caso o corpo A tivesse eletrizado
positivamente, qual seria o sinal da carga
adquirida pelo corpo B ?

22. Solução
Verifica-se que corpos condutores, inicialmente um
eletrizado e outro neutro, depois de entrarem em contato
apresentam cargas de sinais iguais.
Assim:
a) O corpo B fica eletrizado negativamente porque o corpo
A transfere elétrons para ele até que seja estabelecido o
equilíbrio eletrostático.
b) O corpo B fica eletrizado positivamente porque ele
transfere elétrons para o corpo A até que seja estabelecido o
equilíbrio eletrostático.
Resp.:
a) Corpo B: carga negativa
b) Corpo B: carga positiva

23. 3) Uma esfera A com carga 15nC
faz contato com a esfera B, com
carga de –7nC. Sendo informado
que as esferas em questão são
idênticas e metálicas, determine,
em coulomb, as cargas de cadaem coulomb, as cargas de cada
esfera após o contato.

24. Solução
Se esferas condutoras e idênticas forem contactadas,
então suas cargas serão iguais depois do contato.
15nC –7nC q q
Qtotal final = Qtotal inicial
q + q = 15 – 7
2q = 8
q + q = 15 – 7
2q = 8
q = 8/2
q = 4 nC
q = 4.10-9C
Resp.: Esfera A: carga 4.10-9C
Esfera B: carga 4.10-9C

25. LEI DE COULOMB
Em 1785, Coulomb formulou a lei
que rege as interações entre partículas
eletrizadas.

26. A intensidade da força de interação
eletrostática (força elétrica:Fe) entre duas
partículas eletrizadas é dada pela fórmula:
Fe = K.IQI.IqI
d2
onde, K: constante eletrostática do meio
IQI e IqI: módulos das cargasIQI e IqI: módulos das cargas
d: distância entre as partículas
ATENÇÃO !!!
A intensidade da força elétrica é diretamente
proporcional ao produto dos módulos das cargas e
inversamente proporcional ao quadrado da distância
entre as partículas.

27. VAMOS RESOLVER !!!
1) Sejam duas partículas eletrizadas com
cargas Q=2µC e q=–3nC.Tais esferas
estão no vácuo e a distância entre elas é
1 metro. Calcule a intensidade da força
elétrica que uma carga exerce sobre aelétrica que uma carga exerce sobre a
outra. Dado: Constante eletrostática do
vácuo (K) = 9.109 N.m²/C²

28. Solução
Dados: IQI = 2µC = 2.10-6 C
IqI = 3nC = 3.10-9 C
d = 1 m
K = 9.109 unidades do SI
Pela Lei de Coulomb:
Fe = K.IQI.IqI
d2d2
Fe = 9.109.2.10-6.3.10-9
12
Fe = 54.10-6 N
Fe = 5,4.10-5 N
Resp.: Fe = 5,4.10-5 N

29. 2) Na tabela temos informações sobre cargas
elétricas pontuais (ou puntiformes) localizadas no
vácuo e a distância entre cada par de cargas. Por
sua vez, F1, F2 e F3 correspondem aos módulos
das forças de interação eletrostática entre
cargas Q e q, 3Q e 5q e Q e q,
respectivamente.
Cargas Distância Força elétrica
a) Compare F2 e F1.
b) Compare F3 e F1.
Q e q d F1
3Q e 5q d F2
Q e q 2d F3

30. Solução
Com base na Lei de Coulomb, Fe = K.IQI.IqI , temos:
d2
F1 = K.Q.q
d2
a) F2 = K.3Q.5q = 15. K.Q.q = 15.F1 , ou seja, F2=15.F1
d2 d2
b) F3 = K.Q.q = K.Q.q = 1. K.Q.q = 1.F1 , isto é, F3 = 1.F1
(2d)2 4d2 4 d² 4 4
Resp.: a) F2 é 15 vezes maior do que F1.
b) F3 é a quarta parte de F1.

31. QUESTÃO ENEM
Chama-se carga elétrica elementar, indicada por e, a menor
quantidade de carga elétrica isolada existente na natureza. Em módulo,
as cargas do próton e do elétron são iguais a carga elementar e. O valor
da carga elétrica elementar (e = 1,6.10–19 C) foi determinado por Robert
Millikan (norte-americano, 1868-1953) em 1909. Por esse brilhante
trabalho experimental Millikan foi laureado com o Premio Nobel de Física
de 1923. Na década de 1960 Murray Gell-Mann (norte-americano, n.
1929) - Prêmio Nobel de Física de 1969 por seus estudos sobre
partículas subatômicas - levantou a hipótese da existência do quarks. Os
quarks são partículas elementares (experimentalmente detectadas a partir
da década de 1970) formadoras dos prótons e dos nêutrons. Apesar de
existirem 6 tipos de quarks, somente os quarks up e down entram naexistirem 6 tipos de quarks, somente os quarks up e down entram na
composição de prótons e nêutrons. O próton é formado por dois quarks
up e um quark down, por sua vez em cada nêutron há um quark up e dois
quarks up.
A partir dessas informações, é correto concluir, com relação à
carga elementar e, que a carga elétrica dos quarks up e down são,
nesta ordem:
A) + 2e/3 e + 1e/3
B) + 1e/3 e + 2e/3
C) + 1e/3 e – 2e/3
D) – 2 e/3 e + 1e/3
E) + 2e/3 e – 1e/3

32. Solução
1 próton = 2 quarks up + 1 quark down
1 nêutron = 1 quark up + 2 quarks down.
Sabemos que:
Carga elétrica do próton = + 1,6.10–19 C = + e (carga elementar)
Carga elétrica do nêutron = zero (carga nula).
Testando as alternativas:
A) Próton: 2.(+ 2e/3) + 1.(+ 1e/3) = + 4e/3 + 1e/3 = + 5e/3 (Falsa)
B) Próton: 2.(+ 1e/3) + 1.(+ 2e/3) = + 2e/3 + 2e/3 = + 4e/3 (Falsa)
C) Próton: 2.(+ 1e/3) + 1.(– 2e/3) = + 2e/3 – 2e/3 = zero (Falsa)
D) Próton: 2.(– 2e/3) + 1.(+ 1e/3) = – 4e/3 +1e/3 = – 3e/3 = – e (Falsa)
E) Próton:2.(+2e/3) + 1.(–1e/3) = +4e/3 – 1e/3) = + 3e/3 = +e (Verdadeira)
Nêutron: 1.(+2e/3) + 2.(– 1e/3) = + 2e/3 – 2e/3 = zero (Verdadeira)
Resposta: E