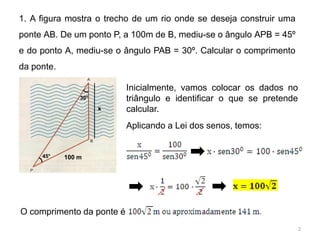
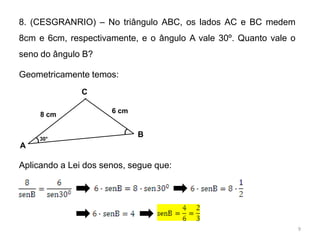
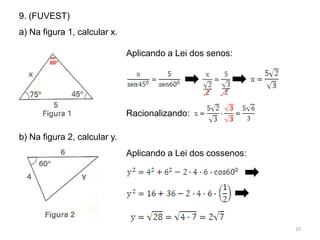
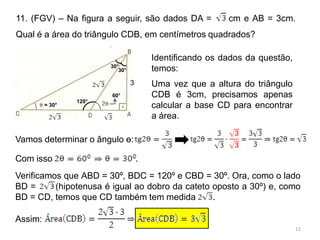
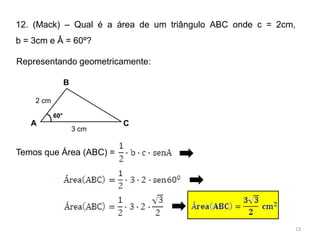
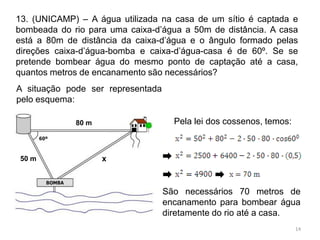
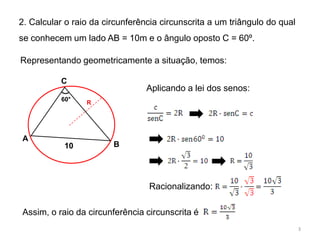
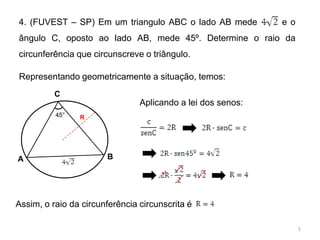
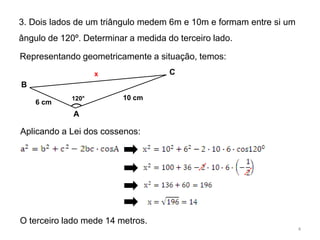
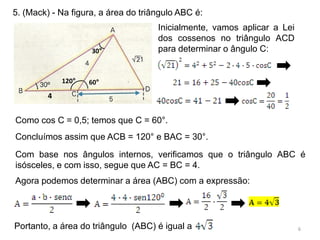
1. O comprimento da ponte é calculado aplicando a Lei dos Senos ao triângulo formado pelos pontos A, B e P. 2. O raio da circunferência circunscrita é igual a 10m dividido pelo seno de 60 graus. 3. Aplicando a Lei dos Cossenos, o terceiro lado do triângulo cujos outros dois lados medem 6m e 10m e formam um ângulo de 120° entre si é 14m.

1. Resolução comentada
Lista sobre lei dos senos e lei dos cossenos
1

2. 1. A figura mostra o trecho de um rio onde se deseja construir uma
ponte AB. De um ponto P, a 100m de B, mediu-se o ângulo APB = 45º
e do ponto A, mediu-se o ângulo PAB = 30º. Calcular o comprimento
da ponte.
Inicialmente, vamos colocar os dados no
30° triângulo e identificar o que se pretende
x calcular.
Aplicando a Lei dos senos, temos:
45° 100 m
O comprimento da ponte é
2

3. 2. Calcular o raio da circunferência circunscrita a um triângulo do qual
se conhecem um lado AB = 10m e o ângulo oposto C = 60º.
Representando geometricamente a situação, temos:
C
Aplicando a lei dos senos:
60°
R
A
10 B
Racionalizando:
Assim, o raio da circunferência circunscrita é
3

4. 3. Dois lados de um triângulo medem 6m e 10m e formam entre si um
ângulo de 120º. Determinar a medida do terceiro lado.
Representando geometricamente a situação, temos:
x C
B
120° 10 cm
6 cm
A
Aplicando a Lei dos cossenos:
O terceiro lado mede 14 metros.
4

5. 4. (FUVEST – SP) Em um triangulo ABC o lado AB mede eo
ângulo C, oposto ao lado AB, mede 45º. Determine o raio da
circunferência que circunscreve o triângulo.
Representando geometricamente a situação, temos:
C
Aplicando a lei dos senos:
45° R
A B
Assim, o raio da circunferência circunscrita é
5

6. 5. (Mack) - Na figura, a área do triângulo ABC é:
Inicialmente, vamos aplicar a Lei
dos cossenos no triângulo ACD
30° para determinar o ângulo C:
120° 60°
4
Como cos C = 0,5; temos que C = 60°.
Concluímos assim que ACB = 120° e BAC = 30°.
Com base nos ângulos internos, verificamos que o triângulo ABC é
isósceles, e com isso, segue que AC = BC = 4.
Agora podemos determinar a área (ABC) com a expressão:
Portanto, a área do triângulo (ABC) é igual a 6

7. 6. (UNIRIO) – Deseja-se medir a distância entre duas cidades B e C
sobre um mapa, sem escala. Sabe-se que AB = 80km e AC = 120km,
onde A é uma cidade conhecida, como mostra a figura. Logo, a
distância entre B e C, em km, é:
a) menor que 90 x
b) maior que 90 e menor que 100
c) maior que 100 e menor que 110 80
d) maior que 110 e menor que 120
120
e) maior que 120
Vamos introduzir os dados do problema no triângulo ABC:
Aplicando a Lei dos cossenos:
Como ; temos que
7

8. 7. (FEI) – Calcule c, sabendo que a = 4, b = e C = 45º.
4=
45°
Vamos introduzir os dados do problema no triângulo ABC:
Aplicando a Lei dos cossenos, temos:
Concluímos que a medida do lado c é
8

9. 8. (CESGRANRIO) – No triângulo ABC, os lados AC e BC medem
8cm e 6cm, respectivamente, e o ângulo A vale 30º. Quanto vale o
seno do ângulo B?
Geometricamente temos:
C
6 cm
8 cm
30°
B
A
Aplicando a Lei dos senos, segue que:
9

10. 9. (FUVEST)
a) Na figura 1, calcular x.
Aplicando a Lei dos senos:
60°
Racionalizando:
b) Na figura 2, calcular y.
Aplicando a Lei dos cossenos:
10

11. 10. (PUC – MG) – Na figura, AB = 5dm, AD = dm, DBC = 60º e
DCA = 90º. Qual é a medida de CD, em decímetros?
Vamos colocar os dados no triângulo e
identificar o que se pretende calcular.
30° Chamando BC de y, segue que BD = 2y.
(A medida da hipotenusa sempre será o
x
2y dobro da medida do cateto oposto ao
ângulo de 30º).
120°
60° . Como o ângulo ABD = 120º, aplicaremos
5 y =5 a Lei dos cossenos em ABD para obter o
valor de y.
Segue que:
Finalmente, do triângulo BCD:
Com isso, a medida de CD é
11

12. 11. (FGV) – Na figura a seguir, são dados DA = cm e AB = 3cm.
Qual é a área do triângulo CDB, em centímetros quadrados?
Identificando os dados da questão,
30°
30° temos:
3 Uma vez que a altura do triângulo
60° CDB é 3cm, precisamos apenas
120°
= 30° calcular a base CD para encontrar
a área.
Vamos determinar o ângulo ɵ:
Com isso .
Verificamos que ABD = 30º, BDC = 120º e CBD = 30º. Ora, como o lado
BD = (hipotenusa é igual ao dobro da cateto oposto a 30º) e, como
BD = CD, temos que CD também tem medida .
Assim:
12

13. 12. (Mack) – Qual é a área de um triângulo ABC onde c = 2cm,
b = 3cm e  = 60º?
Representando geometricamente:
B
2 cm
60°
A C
3 cm
Temos que Área (ABC) =
13

14. 13. (UNICAMP) – A água utilizada na casa de um sítio é captada e
bombeada do rio para uma caixa-d’água a 50m de distância. A casa
está a 80m de distância da caixa-d’água e o ângulo formado pelas
direções caixa-d’água-bomba e caixa-d’água-casa é de 60º. Se se
pretende bombear água do mesmo ponto de captação até a casa,
quantos metros de encanamento são necessários?
A situação pode ser representada
pelo esquema:
80 m Pela lei dos cossenos, temos:
50 m x
São necessários 70 metros de
encanamento para bombear água
diretamente do rio até a casa.
14

15. 14. (FEI) – Num triângulo ABC, BC = a, AC = b, Â = 45º e B = 30º. Qual
é o valor de a, sendo ?
De acordo com os dados:
C
b a
45° 30°
A B
Aplicando a Lei dos senos:
Como , segue que:
Mas , assim
15

16. 15. (Fatec) - Na figura seguinte, qual é a área do triângulo ABC?
1º modo:
. Basta observar que a base do triângulo
h = 0,5
ABC é e a altura é 0,5.
Assim:
2º modo:
16

17. 17