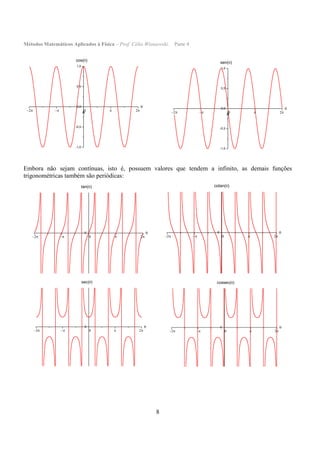
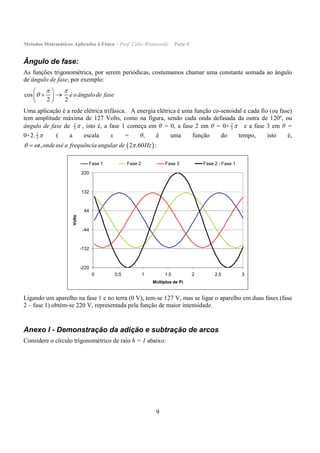
O documento descreve conceitos básicos de trigonometria, incluindo: 1) definições de seno, cosseno e tangente em termos dos lados de um triângulo retângulo; 2) o Teorema de Pitágoras para relacionar os lados de um triângulo retângulo; 3) o uso das funções trigonométricas para resolver problemas de altura e distância.

1. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
1
Trigonometria e relações trigonométricas
Em trigonometria, os lados dos triângulos retângulos
assumem nomes particulares, apresentados na figura ao lado. O lado
mais comprido, oposto ao ângulo de 90º (ângulo reto), chama-se
hipotenusa e os demais se chamam catetos. O cateto que forma o
ângulo θ, na figura, com a hipotenusa é o cateto adjacente ao ângulo
e o outro o cateto oposto.
Teorema de Pitágoras
O grego Pitágoras formulou o seguinte teorema para o triângulo retângulo: a soma do quadrado
dos catetos é igual ao quadrado da hipotenusa. Isto é:
² ² ²x y h 
Relações trigonométricas de ângulos
Os lados do triângulo podem ser relacionados com o ângulo θ, através de relações denominadas
trigonométricas:
Seno do ângulo θ ou sen(θ)
É o quociente entre o cateto oposto ao ângulo θ e a hipotenusa:
 
cateto oposto
sen
hipotenusa
y
h
   .
Cosseno do ângulo θ ou cos(θ)
É o quociente entre o cateto adjacente ao ângulo θ e a hipotenusa;
 
cateto adjacente
cos
hipotenusa
x
h
  
Tangente do ângulo θ ou tan(θ)
É o quociente entre o cateto oposto e o cateto adjacente:
 
cateto oposto
tan
cateto adjacente
y
x
   .
Note que a tangente pode ser escrita como:
sen( ) sen( )
tan( ) tan( )
cos( ) cos( )
y h
x h
 
 
 

   


2. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
2
Funções trigonométricas derivadas
Secante do ângulo θ ou sec(θ)
 
 
1
sec
cos



Co-Secante do ângulo θ ou cosec(θ)
 
 
1
cosec
sen



Co-Tangente do ângulo θ ou cotan(θ)
 
 
1
cotan
tan



A equação fundamental da trigonometria
A equação fundamental da trigonometria surge como um caso particular do teorema de Pitágoras:
   
   
2 2 2
2 2
2 2
1 mas sen e cos
sen cos 1
x y h
x y x y
h h h h
 
 
 
   
      
   
 
.
Desta equação podemos derivar outras. Dividindo ambos os lados por  2
cos  :
 
 
 
   
 
 
2 2
2 2 2
2
2
sen cos 1
cos cos cos
1
tan 1
cos
 
  


 
 
ou, dividindo por  2
sen  :
 
 
 
   
 
 
2 2
2 2 2
2
2
sen cos 1
sen sen sen
1
cotan 1
sen
 
  


 
 

3. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
3
Problema da altura da torre
Um problema interessante é o cálculo da altura da torre a partir dos ângulos α e β.
Fazendo a medição dos ângulos separados pela distância de 10 m mostrado na figura, mediu-se
20 18o o
e   . Então, das funções trigonométricas obtemos:
 
 
tan( ) tan( )
tan( ) tan( )
tan( ) tan( )
mas 10
então:
10 tan( ) tan( )
10tan( )
tan( ) tan( ) 10tan( )
tan( ) tan( )
mas
tan( )
10tan( ) 10tan( ) tan( )
tan( ) tan( ) tan( )
h
h b
b
b a
h
h a
a
b a
a a
a a
h
a
h
h
 
 
 
 

  
 

  
  

   
 
  

 
 
    


  
 tan( ) tan( ) 
Substituindo os valores das tangentes dos ângulos:
tan( ) tan(20 ) 0,367
tan( ) tan(18 ) 0,325
10tan( )tan( )
30,3m
tan( ) tan( )
o
o
h


 
 
 
 
 


4. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
4
Outro problema de medição de altura
A medição da altura do prédio pode ser feita utilizando-se a luz
solar (e a sombra produzida pelo prédio) e uma estaca de altura
conhecida colocada ao lado.
Note que, neste caso, a
tan( ) para o prédio, e é a mesma relação para a estaca:
tan( ) , então,
H
X
h
x
H h h
H X
X x x




  
Port
anto, conhecendo-se o comprimento das sombras e a altura da
estaca, pode-se determinar o valor da altura do prédio H.
Seno, cosseno e tangente como funções reais de variável real
Na figura ao lado, a circunferência foi dividida em ângulos na unidade radianos, onde uma volta inteira
corresponde a 2π radianos ou rad. Isto é, π é a razão entre o diâmetro da circunferência e o comprimento
dela:
2
2
comprimento comprimento
diâmetro raio
comprimento
raio


 


.
Portanto θ tem unidade rad e, neste caso, pode ser usado como
qualquer número nas operações matemáticas, por exemplo:
3,14
2 2 1,41 2,2
4 4 4
se então a operação
 
       
O mesmo não poderia ser feito se θ fosse expresso em graus.
A origem da medida dos ângulo é no eixo das abscissas (x). O eixo
vertical y (ordenadas) corresponde, portanto, a um ângulo de 90º ou θ
= π/2.

5. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
5
Considere o triângulo retângulo à direita do eixo y. O ângulo é θ e o valor das funções trigonométricas
seno e cosseno é:
sen( ) cos( )
y x
h h
  
Agora considere o triângulo retângulo à esquerda do eixo y. O ângulo agora é π – θ. Então:
   
       
sen cos
sen sen cos cos
y x
h h
   
     

   
    
Portanto, a função  sen  é uma função par e  cos  uma função
ímpar.
Agora analisemos o triângulo inferior. Neste caso,
       
       
sen sen 2 cos cos 2
sen sen cos cos
y x
h h
     
   

       
    
Portanto, isto prova novamente o caráter ímpar para a função
cosseno e par para a função seno.
Agora analisemos os casos em que θ =0 e θ = π/2.
Quando θ =0, x será igual ao valor da hipotenusa, isto é, x = h, enquanto que y = 0. Portanto:
   sen 0 0 cos 0 1
y x h
h h h
    
Portanto, podemos construir uma tabela com valores de θ mais comuns:
Θ graus x y  sen
y
h
   cos
x
h
   tan
y
x
 
0 0º h 0 0 1 0
1
2  90º 0 h 1 0 
1
4  45º 2
2 h 2
2 h 2
2
2
2 1
4
3  270º 0 h -1 0 
π 180º -h 0 0 -1 0

6. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
6
Soma e subtração de ângulos.
Algumas propriedades trigonométricas interessantes referem-se à soma ou subtração de ângulos. São elas:
         
         
cos cos cos sen sen
sen sen cos cos sen
     
     
   
    

*Prova no anexo 1
Estas equações podem ser usadas para determinar o valor do seno ou cosseno de ângulos desconhecidos.
Por exemplo, qual o    6sen ou sen 30o
?
sen sen sen cos cos sen
2 6 6 6 6 6 6 6 6 6
1 sen cos cos sen sen cos sen cos cos
6 6 6 6 6 6 6 6 6
         
        
            
                    
            
                  
                      
                  
3 2 2 2
3 2 3
3
sen
6
1 sen 3sen cos cos 1 sen
6 6 6 6 6
1 sen 3sen 1 sen 4sen 3sen
6 6 6 6 6
4sen 3sen 1 0
6 6
Aresoluç

    
    
 
  
   
  
         
              
         
          
                
          
   
     
   
1 2 3
ãodesta equaçãodoterceirograufornece3raízes:
1
sen 1, sen sen
6 6 6 2
comosen está noprimeiroquadrante, asoluça o negativa nãoé valida.
6
1
Portanto sen
6 2
  


     
        
     
 
 
 
 
 
 
Tente fazer      6 12 3cos , sen e sen  
Também podemos obter
 
 
 
 
       
       
       
   
       
   
 
   
   
sen cos cos sen
cos cos
cos cos sen sen
cos cos
sen
tan
cos
sen cos cos sen
tan
cos cos sen sen
tan tan
tan
1 tan tan
   
 
   
 
 
 
 
   
 
   
 
 
 
  

 


 

  
  
 

 





7. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
7
Soma de ângulos iguais
Da primeira equação, fazendo α = θ, obtemos:
         
     
       
       
2 2
2 2 2 2
2 2
cos cos cos sen sen
cos 2 cos sen
cos sen 1 sen 1 cos
cos 2 2cos 1 cos 2 1 2sen
mas
ou
     
  
   
   
    
 
    
   
Da segunda equação, fazendo α = θ, obtemos:
         
     
sen sen cos cos sen
sen 2 2sen cos
     
  
    
 
Periodicidade das funções trigonométricas
As funções seno e cosseno são funções periódicas, cujo período é π.
Note que, ao substituirmos θ nas equações abaixo por  2n  , onde n é um número inteiro, ou o número
de voltas em torno da circunferência, obtemos:
         
         
 
   
   
       
cos cos cos sen sen
cos 2 cos cos 2 sen sen 2
mas sen 2 0 para qualquer
e cos 2 cos 2 1 pois 2 é para qualquer e portanto tem-se múliplos de 2 .
portanto cos 2 cos
sen 2 sen cos 2 cos sen
n n n
n n
n n n par n
n
n n
     
     

  
  
    
    
    

  
 
      
   
2
sen 2 sen
n
n

   
n
Portanto as funções seno e cosseno tem o mesmo valor para 1 2 , 2 2 , 3 2 , ..., 2n               .
Observe no gráfico a periodicidade com que a função se repete:

8. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
8
-1,0
-0,5
0,0
0,5
1,0
A
cos()


-1,0
-0,5
0,0
0,5
1,0
A
sen()


Embora não sejam contínuas, isto é, possuem valores que tendem a infinito, as demais funções
trigonométricas também são periódicas:
0
tan()


0
cotan()


0
sec()


0
cossec()



9. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
9
Ângulo de fase:
As funções trigonométrica, por serem periódicas, costumamos chamar uma constante somada ao ângulo
de ângulo de fase, por exemplo:
cos
2 2
é oângulode fase
 

 
  
 
Uma aplicação é a rede elétrica trifásica. A energia elétrica é uma função co-senoidal e cada fio (ou fase)
tem amplitude máxima de 127 Volts, como na figura, sendo cada onda defasada da outra de 120º, ou
ângulo de fase de 2
3  , isto é, a fase 1 começa em θ = 0, a fase 2 em θ = 0+ 2
3  e a fase 3 em θ =
0+2. 2
3  ( a escala x = θ, é uma função do tempo, isto é,
 , 2 .60t onde é a frequênciaangular de Hz    :
-220
-132
-44
44
132
220
0 0,5 1 1,5 2 2,5 3
Múltiplos de Pi
Volts
Fase 1 Fase 2 Fase 3 Fase 2 - Fase 1
Ligando um aparelho na fase 1 e no terra (0 V), tem-se 127 V, mas se ligar o aparelho em duas fases (fase
2 – fase 1) obtém-se 220 V, representada pela função de maior intensidade.
Anexo I - Demonstração da adição e subtração de arcos
Considere o círculo trigonométrico de raio h = 1 abaixo:

10. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
10
Observando as construções geométricas no círculo trigonométrico acima, podemos deduzir que os
triângulos OMP, OVS e QTS são retângulos e semelhantes. Então, podemos construir algumas relações:
Os triângulos OVS e OMP são semelhantes, logo:
Substituindo as relações (1), (2), (7) na igualdade acima, obtemos:

11. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
11
Os triângulos QTS e OMP são semelhantes, logo:
Substituindo as relações (3), (4) e (7) na igualdade acima, obtemos:
Agora que já construímos algumas relações principais, vamos às demonstrações:
cos(a + b) = cos(a)cos(b) – sen(b)sen(a)
Observando o círculo trigonométrico da figura 1, notamos que:
Podemos concluir também que:
Se substituirmos as relações (5) e (8) na igualdade acima, obteremos:
cos(a – b) = cos(a)cos(b) + sen(b)sen(a)
Da relação (10) temos que:
Se quisermos determinar cos(a – b), podemos escrever a relação acima como:

12. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
12
Mas, se observarmos o círculo trigonométrico da figura 1, deduzimos que:
Então:
Em contrapartida, podemos escrever:
Então teremos:
sen(a + b) = sen(a)cos(b) + sen(b)cos(a)
Sabemos que:
Se fizermos θ = (a + b), teremos:
Da mesma forma, temos:
Temos aqui um cosseno da diferença entre dois arcos e é dado pela relação (11), logo:
Mas, observando a relação (12), vemos algumas similaridades coma relação (13) e podemos escrevê-la
assim:

13. Métodos Matemáticos Aplicados à Física – Prof. Célio Wisniewski. Parte 4
13
sen(a – b) = sen(a)cos(b) – sen(b)cos(a)
Da relação (14) temos que:
Se quisermos determinar sen(a – b), podemos escrever a relação acima como:
No entanto:
e
Fazemos: