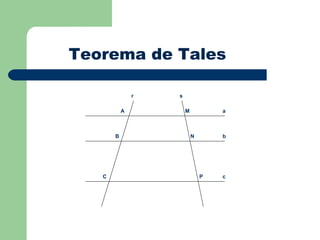
O documento descreve Tales de Mileto, um matemático e filósofo grego do século VI a.C. que contribuiu para a matemática, astronomia e filosofia. O texto também explica o Teorema de Tales, estabelecendo que os segmentos determinados por paralelas cortadas por transversais têm medidas proporcionais.

1. Teorema de Tales Um pouco da vida de Tales O matemático e filosofo grego Tales de Mileto viveu por volta de 624 a 548 a.C. e é considerado um dos “sete sábios” que se conhece da antiguidade. Tales contribuiu tanto na área da Matemática quanto na Astronomia e Filosofia.

2. Utilizando os conhecimentos sobre segmentos sobre segmentos proporcionais, Tales calculou a altura de uma das pirâmides dos faraós do Egito. Para isso, Tales observou o comprimento da sombra da pirâmide e aplicou as propriedades dos segmentos proporcionais. Teorema de Tales

3. Teorema de Tales O teorema linear de Tales estabelece as relações existentes entre os segmentos determinados quando um feixe de paralelas é cortado por duas transversais.

4. Teorema de Tales a b c r s A B C M N P

5. Teorema de Tales Considere as retas a, b e c , paralelas duas a duas, e as transversais r e s . Nesta situação, as medidas dos segmentos determinados em r são diretamente proporcionais às medidas dos segmentos na reta s . AB = MN ou, ainda, AB = BC BC NP MN NP

6. Teorema de Tales Uma aplicação do teorema de Tales está no estabelecimento das condições de semelhança entre dois triângulos retângulos obtidos quando, a partir do lado de um deles, traçamos uma ao outro. Se PQ//CB , então AQ = AP = PQ . Isso AB AC CB quer dizer que os lados são proporcionais e portanto os triângulos são congruentes. A Q B P C