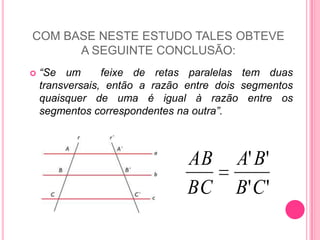
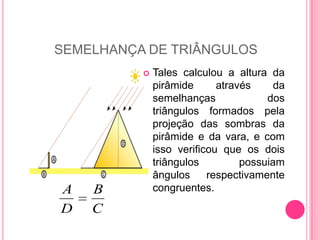
Tales de Mileto observou que os raios solares paralelos formavam triângulos semelhantes com as sombras de objetos e desenvolveu o Teorema de Tales, que estabelece que a razão entre segmentos de uma reta transversal é igual à razão dos segmentos correspondentes de outra reta paralela. Ele aplicou esse princípio para calcular a altura da Grande Pirâmide de Gizé a pedido do faraó. O Teorema de Tales tem diversas aplicações práticas e é uma importante ferramenta matemática.

1. TALES DE MILETO E SEU IMPOTANTE “TEOREMA DE TALES”

2. TEOREMA DE TALESTales observou que os raios solares que chegavam à Terra na posição inclinada eram paralelos, dessa forma, ele concluiu que havia uma proporcionalidade entre as medidas da sombra e da altura dos objetos.

3. COM BASE NESTE ESTUDO TALES OBTEVE A SEGUINTE CONCLUSÃO: “Se um feixe de retas paralelas tem duas transversais, então a razão entre dois segmentos quaisquer de uma é igual à razão entre os segmentos correspondentes na outra”.

4. UM POUCO DE SUA HISTÓRIATales de Miletofoi o primeiro matemático grego do século VII a.C., prósperocomerciante, queemuma de suasviagensaoEgito, foilançado à ele um desafiopeloFaraó e todasuacorte:“Vocêconseguiriamedir a altura de uma das pirâmides de Quéops?Tales de Mileto(640 - 550 a.c.)

5. COMO TALES CALCULOU A ALTURA DA PIRÂMIDE?Segundo as história, Tales fincou uma vara vertical no extremo da sombra projetada pela pirâmide, formando no solo dois triângulos semelhantes, aplicando seus conhecimentos de proporcionalidade e sabendo que a razão entre a altura de um objeto e o comprimento da sombra que esse objeto projeta é sempre a mesma para quaisquer objetos, ele obteve o valor da altura da pirâmide.

6. SEMELHANÇA DE TRIÂNGULOSTales calculou a altura da pirâmide através da semelhanças dos triângulos formados pela projeção das sombras da pirâmide e da vara, e com isso verificou que os dois triângulos possuiam ângulos respectivamente congruentes.

7. AS UTILIDADES DO TEOREMA DE TALESO Teorema de Tales possui diversas aplicações no cotidiano, como por exemplo descobrir a altura de um prédio, de uma casa, de uma árvore, de distâncias inacessíveis, ou até mesmo quando precisamos tomar um remédio e queremos saber a quantia que deve ser administrada, para todos estes experimentos podemos recorrer ao “Teorema de Tales”, ou melhor, a “Regra de Três”.

8. CONCLUSÃOAtravés deste estudo, concluímos que o Teorema de Tales é uma das mais importantes ferramentas matemáticas, que utiliza as noções de semelhança e proporção tanto na geometria, como na área financeira, na biologia, na medicina, e em diversas situações do cotidiano.