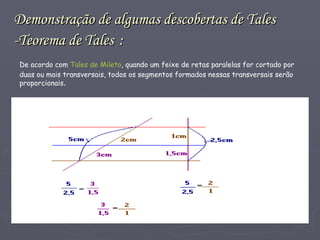
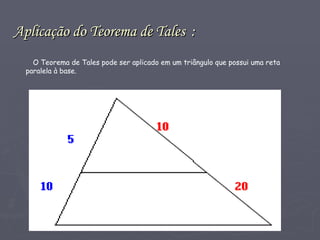
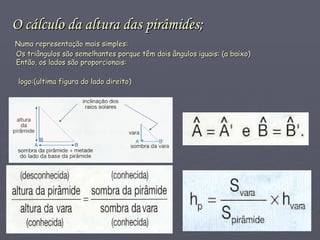
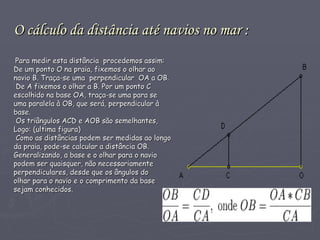
Tales de Mileto foi um filósofo, astrônomo e matemático grego do século VI a.C. considerado o fundador da geometria demonstrativa. Ele fez descobertas fundamentais em matemática, como o teorema de que ângulos opostos pelo vértice são iguais e métodos para calcular a altura de pirâmides e distância de navios. Suas ideias deram início à sistematização da matemática pelos gregos a partir dos conhecimentos egípcios e babilônicos.

1. Matemático Tales de Mileto Alunas:Ana Carolina , Pâmilla karine ,Tais Cristina N°: 02-28-32 9°ano A

2. Introdução: Neste trabalho iremos ver a vida do filósofo e matemático grego Tales de Mileto, que foi simultaneamente geómetra, filósofo e astrônomo, mas celebrizou-se sobretudo como geômetra, dando o seu nome a um famoso teometra de geometria.Também veremos suas descoberta que são fundamentas na matemática

3. Quem foi Tales de Mileto ? Tales de mileto era filósofo, astrônomo e matemático, descobrimos que ele viveu no século VI a.C. Para alguns historiadores da matemática antiga, a geometria demonstrativa iniciou-se com Tales de Mileto, um dos sete sábios da Grécia. Tales é uma figura imprecisa historicamente, pois não sobreviveu nenhuma obra sua. O que sabemos é baseado em antigas referências gregas à história da matemática que atribuem à ele um bom número de descobertas matemáticas definidas. Pouco sabemos sobre a vida e obra de Tales. Supõe-se que começou sua vida como mercador, tornando-se rico o suficiente para dedicar a parte final de sua vida ao estudo e a realização de algumas viagens.

4. Quem foi Tales de mileto ? Supõe-se que viveu algum tempo no Egito onde provavelmente aprendeu geometria e na Babilônia onde entrou em contato com tabelas e instrumentos astronômicos. Faz parte do seu mito o fato de ter previsto o eclipse solar de 585 a.C., embora muitos historiadores da ciência duvidem que os meios existentes na época permitissem tal proeza. Tales foi o primeiro personagem conhecido a quem associam-se descobertas matemáticas. Acredita-se que obteve seus resultados mediante alguns raciocínios lógicos e não apenas por intuição ou experimentação . Através de Tales e sua escola filosófica os gregos começaram a reunir em corpo a ciência matemática que provinha dos Egípcios e Caldeus. Tales de mileto morreu asfixiado pela multidão ao sair de um espetáculo .

5. Descobertas Tales chamou a atenção para o fato de que se duas retas se cortam , então os ângulos opostos pelo vértice são iguais . Ele descobriu vários pontos que ajudam na matemática até hoje: - A demonstração de que os ângulos da base de dois triângulos isósceles são iguais; - O cálculo da altura das pirâmides; - O cálculo da distância até navios no mar; - A demonstração do seguinte teorema: se dois triângulos tem dois ângulos e um lado respectivamente iguais,então são iguais; - A demonstração de que todo diâmetro divide um círculo em duas partes iguais; - A demonstração de que unir qualquer ponto de uma circunferência aos extremos de um diâmetro AB obtém-se um triângulo retângulo em C.

6. Demonstração de algumas descobertas de Tales -Teorema de Tales : De acordo com Tales de Mileto , quando um feixe de retas paralelas for cortado por duas ou mais transversais, todos os segmentos formados nessas transversais serão proporcionais .

7. Aplicação do Teorema de Tales : O Teorema de Tales pode ser aplicado em um triângulo que possui uma reta paralela à base.

8. O cálculo da altura das pirâmides; Numa representação mais simples: Os triângulos são semelhantes porque têm dois ângulos iguais: (a baixo) Então, os lados são proporcionais: logo:(ultima figura do lado direito)

9. O cálculo da distância até navios no mar : Para medir esta distância procedemos assim: De um ponto O na praia, fixemos o olhar ao navio B. Traça-se uma perpendicular OA a OB. De A fixemos o olhar a B. Por um ponto C escolhido na base OA, traça-se uma para se uma paralela à OB, que será, perpendicular à base. Os triângulos ACD e AOB são semelhantes, Logo: (ultima figura) Como as distâncias podem ser medidas ao longo da praia, pode-se calcular a distância OB. Generalizando, a base e o olhar para o navio podem ser quaisquer, não necessariamente perpendiculares, desde que os ângulos do olhar para o navio e o comprimento da base sejam conhecidos.

10. Triângulos isósceles : Seja ABC um triângulo isósceles com os lados AB e AC iguais, e sejam as linhas retas BD e CE produzidas numa linha resta com AB e AC. Digo que o ângulo ABC é igual ao ângulo ACB e o ângulo CBD é igual ao ângulo BCE. Tome-se um ponto arbitrário F na linha Rita BD. Corte-se da linha Rita maior AE uma parte AG igual à linha Rita menor AF e desenhem-se as linhas Rita FC e GB. Como AF é igual a AG e AB é igual a AC então os dois lados FA e AC são iguais aos dois lados GA e AB respectivamente, e compreendem um ângulo igual, o ângulo FAG. Portanto a base FC é igual à base GB, o triângulo AFC é igual ao triângulo AGB e os outros ângulos são iguais aos outros ângulos respectivamente, isto é, os que são opostos a lados iguais, ou seja, o ângulo ACF é igual ao ângulo ABG e o ângulo AFC é igual ao ângulo AGB. Como AF é igual a AG e AB igual a AC então BF é igual a CG. Mas foi demonstrado que FC é igual GB, logo os dois lados BF e FC são iguais aos dois lados CG e GB respectivamente, e o ângulo BFC é igual ao ângulo CGB, enquanto a base BC é comum aos dois. Portanto o triângulo BFC é igual ao triângulo CGB e os outros ângulos são iguais aos outros ângulos, isto é, os que são opostos a lados iguais. Assim, o ângulo FBC é igual ao ângulo GCB e o ângulo BCF é igual ao ângulo CBG. Como foi e mostrado que o triângulo ABG é igual ao triângulo ACF e o ângulo CBG é igual ao ângulo BCF, o outro ângulo ABC é igual ao outro ângulo ACB, os quais estão na base do triângulo ABC. Mas também foi demonstrado que o ângulo FBC é igual ao ângulo GCB os quais estão debaixo da base do triângulo ABC. Assim, em triângulos isósceles os ângulos da as e são iguais e, se as linhas retas iguais forem produzidas, então os ângulos que se formam debaixo da base também são iguais .

11. IMPORTÂNCIA DE TALES # Caráter dedutivo que deu à ciência # Através de Tales e sua escola filosófica os gregos começaram a reunir em corpo a ciência matemática que provinha dos Egípcios e Caldeus # Aumentaram os conhecimentos desta ciência, Matemática, em em diversos sentidos

12. Conclusão: Com este trabalho conhecemos melhor a vida e obra de Tales de Mileto e qual sua importância na matemática, sua descobertas que ajudam a matemática até os dias de hoje, além do seu valiosoo contributo para o seu desenvolvimento da MATEMÁTICA.