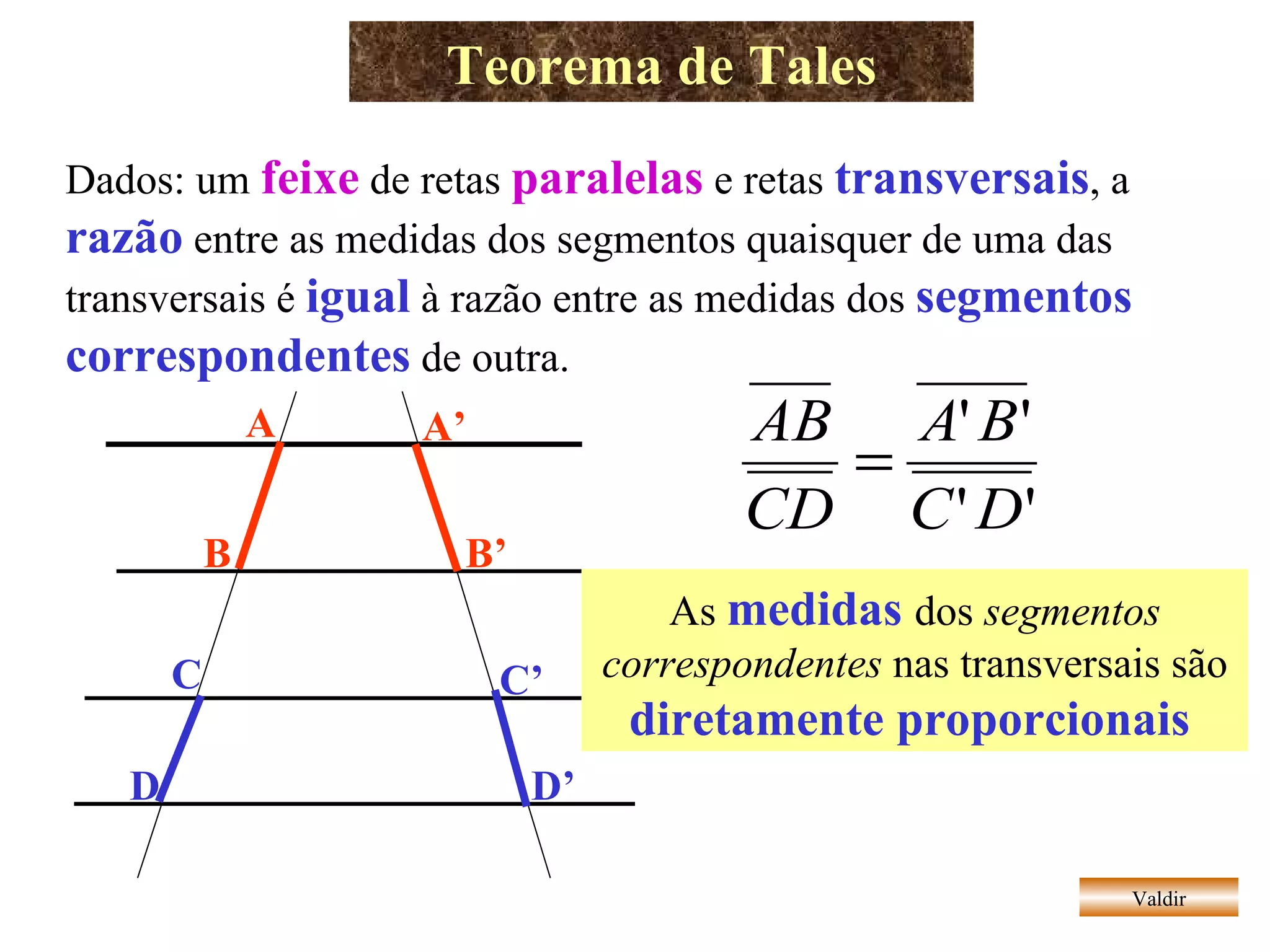
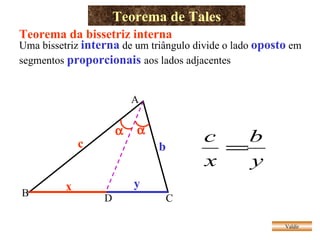
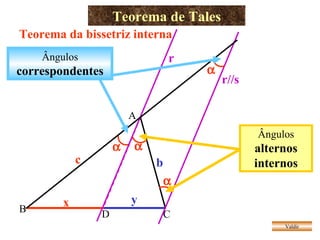
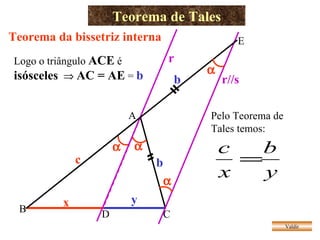
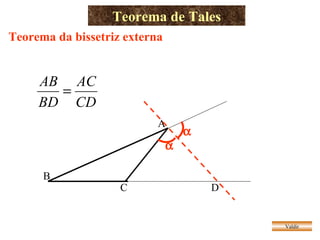
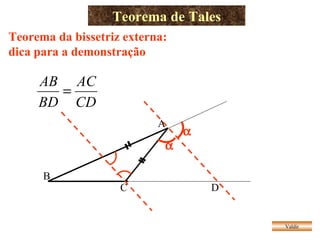
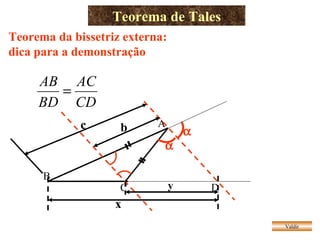
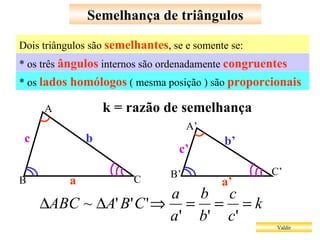
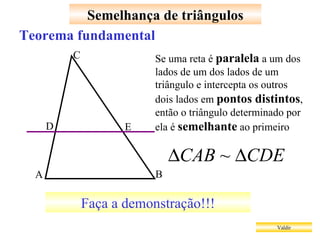
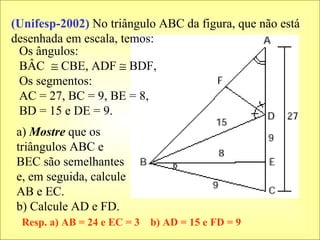
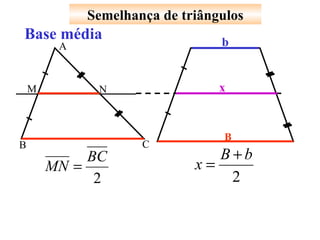
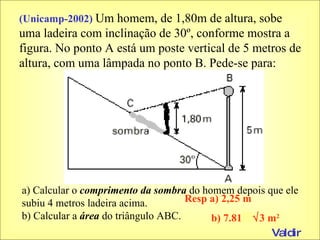
O documento apresenta vários teoremas geométricos, incluindo: 1) Teorema de Tales, que estabelece que a razão entre segmentos de retas transversais é igual à razão entre os segmentos correspondentes de outra reta paralela; 2) Teorema da bissetriz interna, que divide o lado oposto em segmentos proporcionais aos lados adjacentes; 3) Semelhança de triângulos quando possuem ângulos correspondentes congruentes ou lados proporcionais.

1. Teorema de Tales Valdir Dados: um feixe de retas paralelas e retas transversais , a razão entre as medidas dos segmentos quaisquer de uma das transversais é igual à razão entre as medidas dos segmentos correspondentes de outra. As medidas dos segmentos correspondentes nas transversais são diretamente proporcionais A B A’ B’ C D C’ D’

2. Teorema de Tales Valdir c b D Teorema da bissetriz interna Uma bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes A B C   x y

3. Teorema de Tales Valdir Teorema da bissetriz interna r r//s Ângulos alternos internos Ângulos correspondentes A B C   c b D x y  

4. Teorema de Tales Valdir Teorema da bissetriz interna E Logo o triângulo ACE é isósceles  AC = AE = b b Pelo Teorema de Tales temos: A B C   c b D x y r r//s  

5. Teorema de Tales Valdir Teorema da bissetriz externa D A B C  

6. Teorema de Tales Valdir Teorema da bissetriz externa: dica para a demonstração D A B C  

7. Teorema de Tales Valdir Teorema da bissetriz externa: dica para a demonstração y A B C   D c b x

8. Semelhança de triângulos Valdir * os três ângulos internos são ordenadamente congruentes Dois triângulos são semelhantes , se e somente se: * os lados homólogos ( mesma posição ) são proporcionais a a’ b’ b c c’ k = razão de semelhança A B C A’ B’ C’

9. Semelhança de triângulos Valdir Teorema fundamental Se uma reta é paralela a um dos lados de um dos lados de um triângulo e intercepta os outros dois lados em pontos distintos , então o triângulo determinado por ela é semelhante ao primeiro Faça a demonstração!!! A B C D E

10. Semelhança de triângulos Valdir Casos ( ou critérios ) de semelhança 1- dois ângulos ordenadamente congruentes 2- LAL lados proporcionais e ângulos entre eles congruentes 3- LLL lados homólogos proporcionais

11. a) Mostre que os triângulos ABC e BEC são semelhantes e, em seguida, calcule AB e EC. b) Calcule AD e FD. Os ângulos: BÂC  CBE, ADF  BDF, Os segmentos: AC = 27, BC = 9, BE = 8, BD = 15 e DE = 9. (Unifesp-2002) No triângulo ABC da figura, que não está desenhada em escala, temos: Resp. a) AB = 24 e EC = 3 b) AD = 15 e FD = 9

12. Semelhança de triângulos Base média A B C M N B b x

13. (Acafe-SC-2001)Uma pessoa caminha sobre uma rampa inclinada (inclinação constante) de 3,5m de altura. Após caminhar 12m sobre ela, se encontra a 1,5m de altura em relação ao solo. Para atingir o ponto mais alto da rampa, quantos metros esta pessoa deve ainda caminhar? A)16 B)28 C) 9 D)14 E)24

14. (Unicamp-2002) Um homem, de 1,80m de altura, sobe uma ladeira com inclinação de 30º, conforme mostra a figura. No ponto A está um poste vertical de 5 metros de altura, com uma lâmpada no ponto B. Pede-se para: a) Calcular o comprimento da sombra do homem depois que ele subiu 4 metros ladeira acima. b) Calcular a área do triângulo ABC. Resp a) 2,25 m b) 7.8125  3 m 2 Valdir

15. (Ita-2000)Considere a circunferência inscrita num triângulo isósceles com base de 6cm e altura de 4cm. Seja t a reta tangente a esta circunferência e paralela à base do triângulo. O segmento de t compreendido entre os lados do triângulo mede A) 1cm B) 1,5cm C) 2cm D) 2,5cm E) 3cm A) 1cm B) 1,5cm C) 2cm D) 2,5cm E) 3cm