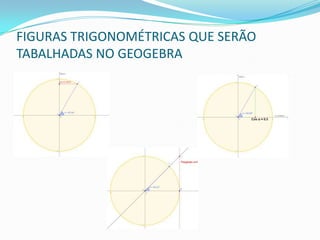
Este documento descreve três atividades para explorar funções trigonométricas usando o Geogebra. A Atividade 1 explora o seno movendo um ponto P ao redor de uma circunferência trigonométrica. A Atividade 2 explora o cosseno da mesma forma. A Atividade 3 explora a tangente usando um eixo tangente. Os objetivos são entender como os valores dessas funções variam com o ângulo.

1. ATIVIDADES TRIGONOMÉTRICASTRABALHANDO COM SENO,COSSENO E TANGENTE NO CICLO TRIGONOMÉTRICO CONTRUIDO NO GEOGEBRA

2. ATIVIDADE 1Seno na Circunferência Trigonométrica1)Movimente o ponto P livremente sobre a circunferência, em quais quadrantes o valor do Seno é positivo e em quais quadrantes o valor é negativo? Você consegue esclarecer porque isso ocorre?2) Encontre dois ângulos tais que os valores de seno sejam iguais, por que isso ocorre?3) Alguns ângulos são chamados ângulos notáveis: 30º 45º , 60º ,verifique na circunferência trigonométrica o valor dos senos de cada um desses ângulos.4) Qual o valor máximo e o valor mínimo para o Seno de P ? Como você explica esse fato?

3. ATIVIDADE 1Explorando o Cosseno na Circunferência Trigonométrica1)Movimente o ponto P livremente sobre a circunferência, em quais quadrantes o valor do Cosseno é positivo e em quais quadrantes o valor é negativo? Você consegue esclarecer porque isso ocorre?2) Encontre dois ângulos tais que o valor de cosseno seja igual, por que isso ocorre?3) Alguns ângulos são chamados ângulos notáveis: 30º 45º , 60º ,verifique na circunferência trigonométrica o valor dos cossenos de cada um desses ângulos.4) Qual o valor máximo e o valor mínimo para o Cosseno de P ? Comovocê explica esse fato?

4. ATIVIDADE 1Explorando a Tangente na Circunferência Trigonométrica1)Movimente o ponto P livremente sobre a circunferência, e verifique o que ocorre com o ponto T, em quais quadrantes o valor da Tangente de P é positivo e em quais quadrantes o valor é negativo?2) Encontre dois ângulos tais que o valor da tangente seja igual, por que isso ocorre?3) Alguns ângulos são chamados ângulos notáveis: 30º 45º , 60º ,verifique na circunferência trigonométrica o valor da tangente de cada um desses ângulos.4) Você consegue determinar o valor da Tangente de 90º e 270º?Justifique sua resposta.

5. OBJETIVOS DAS ATIVIDADESSeno na Circunferência TrigonométricaExplorar o seno como a ordenada do ponto P da circunferência unitária C, observando, entre outros, que para todo ponto P(x,y) C , temos que -1 x 1. Neste caso é o ângulo formado entre o ponto A (1,0) pertencente à circunferência unitária e um ponto P qualquer pertencente à circunferência. Será explorado por meio de um applet (objeto de aprendizagem de simulação) gerado no software Geogebra.

6. Explorando o Cosseno na Circunferência TrigonométricaExplorar o cosseno como a abscissa do ponto P da circunferência unitária C, observando, entre outros, que para todo ponto P(x,y) C , temos que -1 x 1. Neste caso é o ângulo formado entre o ponto A (1,0) pertencente à circunferência unitária e um ponto P qualquer pertencente à circunferência.

7. Explorando a Tangente na Circunferência TrigonométricaPromover a exploração do conceito tangente, por meio de um eixo tangente ao ponto (1,0) da circunferência trigonométrica.Assim o valor da tangente será obtido através do ponto T que será a intersecção do eixo tangente com o prolongamento da reta que passa pela origem e pelo ponto P pertencente à circunferência.

8. FIGURAS TRIGONOMÉTRICAS QUE SERÃO TABALHADAS NO GEOGEBRA