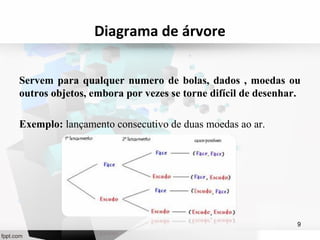
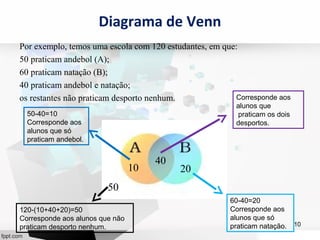
O documento discute probabilidades e fornece exemplos de conceitos básicos como espaço amostral, acontecimentos, tipos de acontecimentos, a lei de Laplace e formas de representar probabilidades como tabelas de dupla entrada, diagramas de árvore e diagramas de Venn.

1. Probabilidades
Prof.
Disciplina: Matemática
Modulo A7 - Probabilidades

2. O que são probabilidades?
• Existem dois tipos de experiências:
• Uma probabilidade é uma forma de medir as hipóteses que um dado
acontecimento tem de ocorrer.
 As probabilidades interessam-se pelas experiências aleatórias!
2
Aleatórias Deterministas
Quando, à partida, não sabemos
o resultado.
Exemplos: Lançamento de uma
moeda, totoloto, extração de uma
carta, etc..
Quando, à partida, já
conhecemos o resultado.
Exemplos: furar um balão cheio,
deixar cair um prego num copo
de água, etc..

3. Espaço de resultados
O espaço de resultados ou espaço amostral é o conjunto de todos os
resultados possíveis de uma experiência aleatória.
Representa-se por E, S ou Ω.
Exemplo: Lançamento de um dado
Espaço amostral = E= {1,2,3,4,5,6}
3

4. Acontecimentos
• Um acontecimento é um subconjunto do espaço amostral.
• Um acontecimento identifica-se como o conjunto dos seus casos
favoráveis.
4
Tipos de Acontecimentos
Elementares: quando só tem um elemento.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
A: “sair número 3”
A={3}
Compostos: quando tem mais que um elemento.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
B: “sair número ímpar”
B={1,3,5}

5. 5
Tipos de acontecimentos
Equiprováveis/Igualmente prováveis: têm a mesma probabilidade de
acontecer.
Exemplo:
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
C: “sair número par”
D: “sair número ímpar”
C e D são equiprováveis!
Certos: verificam-se sempre.
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
E: “sair número inteiro positivo inferior a 7”
E= {1,2,3,4,5,6}
Impossíveis: nunca se verificam.
Experiência: Lançamento de um dado
E = {1,2,3,4,5,6}
F: “Sair número inteiro positivo superior a 7”
F= {}

6. Lei de Laplace
• A probabilidade de realização de um acontecimento A é igual ao quociente
entre o número de casos favoráveis à sua realização e o numero total de
casos possíveis.
Nasceu em Beaumont-en-Auge, a 23 de
março de 1749 e morreu em Paris, a 5 de
março de 1827. Foi um matemático,
astrónomo e físico francês que, entre outras criações,
fundou a Lei de Laplace.
6
Simon Laplace

7. Probabilidades
 A probabilidade de um acontecimento impossível é 0 ou 0%.
 A probabilidade de um acontecimento certo é 1 ou 100%
 Em qualquer experiência, a probabilidade de um acontecimento A é um
número maior ou igual a 0 mas menor ou igual a 1, ou seja:
 Se A é um acontecimento impossível, mas não certo: 0<P(A)<1.
 Quando dois acontecimentos A e B não podem ocorrer ao mesmo tempo:
P(A ou B) = P(A) + P(B).
7

8. Tabela de dupla entrada
Só serve no caso de haver apenas dois objetos (moedas, dados,
bolas, piões...).
Exemplo: lançamento consecutivo de dois dados.
8

9. Diagrama de árvore
Servem para qualquer numero de bolas, dados , moedas ou
outros objetos, embora por vezes se torne difícil de desenhar.
Exemplo: lançamento consecutivo de duas moedas ao ar.
9

10. Diagrama de Venn
Por exemplo, temos uma escola com 120 estudantes, em que:
50 praticam andebol (A);
60 praticam natação (B);
40 praticam andebol e natação;
os restantes não praticam desporto nenhum.
10
50-40=10
Corresponde aos
alunos que só
praticam andebol.
Corresponde aos
alunos que
praticam os dois
desportos.
60-40=20
Corresponde aos
alunos que só
praticam natação.
120-(10+40+20)=50
Corresponde aos alunos que não
praticam desporto nenhum.
10
40
20
50

11. FIM 
11