1. O documento apresenta um resumo teórico sobre conjuntos e operações entre conjuntos, com o objetivo de preparar os alunos para o vestibular de matemática. 2. São abordados temas como representação de conjuntos, igualdade e inclusão entre conjuntos, conjunto das partes, operações de união, interseção e diferença entre conjuntos. 3. O resumo é organizado em tópicos e subitens, com exemplos ilustrativos para cada conceito apresentado.

1. Pré-vestibulinho
Matemática
Matemática para Vestibulinho
Prof. Wlad
Conteúdo programático
1. Conjuntos ............................................................................................................................. 02
2.Números naturais, inteiros, racionais e irracionais.................................................................... 08
3. Potenciação, radiciação........................................................................................................... 13
4. Expressões algébricas............................................................................................................. 14
5. Produtos notáveis e fatorações............................................................................................... 16
6. Razões e proporções............................................................................................................... 17
7. Regra de Três ......................................................................................................................... 20
8. Porcentagem. Problemas de aplicações................................................................................... 23
9. Equações de 1º e 2º graus. Problemas de aplicações................................................................ 27
10. Sistemas de equações de 1º grau........................................................................................... 30
11. Plano cartesiano ................................................................................................................... 32
12. Função do 1º Grau ............................................................................................................... 33
13. Função exponencial ............................................................................................................. 35
14. Elementos fundamentais da geometria plana e semelhança de figuras planas........................ 37
15. Relações métricas no triângulo retângulo.............................................................................. 43
16. Razões trigonométricas ........................................................................................................ 46
17. Áreas de figuras planas......................................................................................................... 50
18. Sólidos Geométricos .......................................................................................................... 53
19. Análise combinatória e probabilidade.................................................................................... 56
20. Noções de estatística............................................................................................................ 58
21. Lógica e seqüências ............................................................................................................. 63
Anexos .................................................................................................................................... 67
EDIÇÃO 2010
Resumo teórico 1

2. Pré-vestibulinho
Matemática
a) Extensão ou Enumeração
1. CONJUNTOS
Quando o conjunto é representado por uma listagem
1.1. Introdução ou enumeração de seus elementos. Devem ser escritos
entre chaves e separados por vírgula ou ponto-e-vírgula.
a) Conjunto
Exemplos:
A noção de conjunto em Matemática é praticamente
a mesma utilizada na linguagem cotidiana:  Conjunto dos nomes de meus filhos: {Larissa,
agrupamento, classe, coleção. Por exemplo: Júnior, Thiago, Juliana, Fabiana};
 Conjunto dos meses com menos de 31 dias:
 Conjunto das letras maiúsculas do alfabeto; {fevereiro, abril, junho, setembro, novembro};
 Conjunto dos números inteiros pares;  Conjunto dos números pares inteiros maiores do
 Conjunto dos dias da semana; que 8 e menores do que 22: {10; 12; 14; 16; 18;
20}.
b) Elemento
Observações:
Cada membro ou objeto que entra na formação do
conjunto. Assim: 1. Na representação por extensão cada elemento
deve ser escrito apenas uma vez;
 V, I, C, H, E são elementos do primeiro conjunto 2. É uma boa prática adotar a separação dos
acima; elementos em conjuntos numéricos como
 2, 4, 6 são elementos do segundo; sendo o ponto-e-vírgula, para evitar confusões
 Sábado, Domingo do terceiro; com as casas decimais: {2;3;4} e {2,3;4};
3. Esta representação pode, também, ser adotada
para conjuntos infinitos em que se evidencia a lei
c) Pertinência entre elemento e conjunto de formação de seus elementos e colocando-se
reticências no final: {2, 4, 6, 8, 10, …};
4. Representação semelhante pode ser adotada para
Por exemplo, V é um elemento do conjunto das
conjuntos finitos com um grande número de
letras maiúsculas do alfabeto, ou seja, V pertence àquele
elementos: {0, 1, 2, 3, …, 100}.
conjunto. Enquanto que v não pertence.
b) Propriedade dos Elementos
Como se vê são conceitos intuitivos e que se supõe
sejam entendidos (evidentes) por todos.
Representação em que o conjunto é descrito por uma
propriedade característica comum a todos os seus
Notação
elementos. Simbolicamente:
Conjunto: Representado, de forma geral, por uma letra
A = {x | x tem a Propriedade P}
maiúscula A, B, C, …
Elemento: Por uma letra minúscula a, b, c, x, y, z, … e lê-se: A é o conjunto dos elementos x tal que (|) x tem a
propriedade P.
Pertinência: Sejam A um conjunto e x um elemento. Se x é
um elemento de A (ou x pertence a A) indicamos por: Exemplos:
 A = {x | x é um time de futebol do Campeonato
Brasileiro de 2006};
 B = {x | x é um número inteiro par e 8 < x < 22}.
Caso contrário, ou seja, se x não é um elemento de A (ou x
Último exemplo do item a) acima;
não pertence a A) escrevemos:
 C = {x | x é um deputado federal eleito em 2006}.
c) Diagrama de Euler-Venn
1.2. Representações de Conjuntos Um conjunto pode ser representado por meio de uma linha
fechada e não entrelaçada, como mostrado na figura
abaixo. Os pontos dentro da linha fechada indicam os
elementos do conjunto.
Resumo teórico 2

3. Pré-vestibulinho
Matemática
Igualdade de Conjuntos
Dois conjuntos A e B são iguais quando todo elemento de A
pertence a B e, reciprocamente, todo elemento de B
pertence a A:
Conjunto Unitário e Conjunto Vazio
Embora o conceito intuitivo de conjunto nos remeta à idéia Observações:
de pluralidade (coleção de objetos), devemos considerar a
existência de conjunto com apenas um elemento,
1. A título de ilustração: O A invertido na expressão
chamados de conjuntos unitários, e o conjunto sem
acima significa “para todo”;
qualquer elemento, chamado de conjunto vazio (Ø).
2. {a, b, c, d} = {d, b, a, c}. O que demonstra que a
noção de ordem não interfere na igualdade de
O conjunto vazio é obtido quando descrevemos um conjuntos;
conjunto onde a propriedade P é logicamente falsa. 3. É evidente que para A ser diferente de B é
suficiente que um elemento de A não pertença a B
Exemplos de Conjuntos Unitários: ou vice-versa: A = {a, b, c} é diferente de B = {a, b,
c, d}.
 Conjunto dos meses do ano com menos de 30 dias:
{fevereiro};
 Conjunto dos números inteiros maiores do que 10
e menores do que 12: {11}; Subconjunto
 Conjunto das vogais da palavra blog: {o}.
Um conjunto A é um subconjunto de (está contido em) B se,
Exemplos de Conjuntos Vazios: e somente se, todo elemento x pertencente a A também
pertence a B:
 { x | x > 0 e x < 0 } = Ø;
 Conjunto dos meses com mais de 31 dias;

2
{ x | x = -1 e x é um número real} = Ø.
onde a notação significa “A é subconjunto de B”
Conjunto Universo ou “A está contido em B” ou “A é parte de B”. A leitura da
notação no sentido inverso é feita como “B contém A”.
É o conjunto ao qual pertencem todos os elementos
envolvidos em um determinado assunto ou estudo, e é Observe que a abertura do sinal de inclusão fica
simbolizado pela letra U. sempre direcionado para o conjunto “maior”. Na forma de
diagrama é representado como:
Assim, se procuramos determinar as soluções reais de uma
equação do segundo grau, nosso conjunto Universo U é R
(conjunto dos números reais); se estamos interessados em
determinar os deputados federais envolvidos com o
mensalão, nesse caso o universo U tem como elementos
todos os deputados federais da atual legislatura.
Portanto, é essencial, que ao descrever um conjunto através
de uma propriedade P, fixemos o conjunto universo em que
estamos trabalhando, escrevendo:
Resumo teórico 3

4. Pré-vestibulinho
Matemática
Exemplos: Observações:
 {1; 2; 3} C {1; 2; 3; 4; 5; 6} 1. Enfatizo, apesar de colocado na própria definição,
 Ø C {a, b}; que os elementos de P(E) são conjuntos;
 {a, b} C {a, b}; 2. Assim, deve-se ter atenção quanto ao emprego dos
 {a, b, c} ¢ {a, c, d, e}, onde ¢ significa “não está símbolos pertence (não pertence) e contido (não
contido”, uma vez que o elemento b do primeiro contido);
conjunto não pertence ao segundo. 3. No primeiro exemplo acima: {a} pertence a P(A) e
{{a}} é um subconjunto de P(A);
Observe que na definição de igualdade de conjuntos está 4. Se definirmos n(E) como sendo o número de
n(E)
explícito que todo elemento de A é elemento de B e vice- elementos do conjunto E, então n(P(E)) = 2 . A
versa, ou seja, que A está contido em B e B está contido em propriedade é válida para conjuntos finitos;
3
A. Assim, para provarmos que dois conjuntos são iguais 5. Veja nos exemplos: n(A) = 3 e n(P(A)) = 8 = 2 , n(B)
2 1
devemos provar que: = 2 e n(P(B)) = 4 = 2 e n(C) = 1 e n(P(C)) = 2 = 2 .
Propriedades da Inclusão 1.3. Operações entre conjuntos
Sejam D, E e F três conjuntos quaisquer. Então valem as
seguintes propriedades: ►União : 
1. Ø C D: O conjunto vazio é subconjunto de qualquer Conjunto união são todos os elementos dos
conjunto; conjuntos relacionados.
2. D C D: Todo conjunto é subconjunto de si próprio
(propriedade Reflexiva);
3. D C E e E C D => D = E: veja acima (propriedade A  B = { x  A ou x  B }
Anti-Simétrica);
4. D C E e E C F => D C F: Se um conjunto é Exemplo 1:
subconjunto de um outro e este é subconjunto de Dados os conjuntos A = { 1, 2, 3, 4,} e B = {0, 2, 4, 5} a
um terceiro, então o primeiro é subconjunto do união desses dois conjuntos é :
terceiro (propriedade Transitiva).
Com exceção da primeira propriedade, a demonstração das A  B = { 0, 1, 2, 3, 4 ,5 }
demais é bastante intuitiva e imediata. Vamos, portanto,
provar a primeira:
Partimos da tese de que se o conjunto vazio não é um
subconjunto de D, então é necessário que pelo menos um
elemento desse conjunto não esteja contido no conjunto D.
Como o conjunto vazio não possui nenhum elemento, a
sentença Ø ¢ D é sempre falsa. Logo, o conjunto vazio está
contido em D é sempre verdadeira.
A B
Conjunto das Partes
Chama-se Conjunto das Partes de um conjunto E - P(E) - o Exemplo 2:
conjunto formado por todos os subconjuntos de E: Dados os conjuntos A = {1,2,3} e B = {1,2,3,4,5} a união
desses conjuntos é:
Exemplos: A  B = { 0, 1, 2, 3, 4 ,5 }
nesse caso podemos dizer que A  B = B
 Se A = {a, b, c}, então P(A) = {Ø, {a}, {b}, {c}. {a.b},
{a.c}. {b,c}, {a,b,c}}
 Se B = {a, b}, então P(B) = {Ø, {a}, {b}, {a,b}};
 Se C = {a}, então P(C) = {Ø, {a}}.
Resumo teórico 4

5. Pré-vestibulinho
Matemática
► Intersecção:  Exemplo 1:
Os elementos que fazem parte do conjunto A = {1, 3, 5, 7} e B = {1, 3, 8 } a diferença dos conjuntos é:
intersecção são os elementos comuns aos conjuntos
relacionados.
A B={ xA e xB} A–B
Exemplo 1:
Dados dois conjuntos A = {1, 2, 3, 4} e B = {2, 3, 8}, se
A – B = { 1, 2 }
pedimos a intersecção deles teremos:
A  B = { 2, 3 } , dizemos que A “inter” B é igual a 2 e
3.
B–A
B–A={8}
A B
Exemplo 2:
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7, -8, -9}, se
pedirmos a intersecção deles teremos:
Exemplo 2:
A = {1, 2, 3, 4, 5} e B = {8, 9, 10} a diferença dos conjuntos
é:
A – B = { 1, 2, 3, 4, 5 }
Exemplo 3:
A = {1, 2, 3} e B = {1, 2, 3, 4, 5}a diferença dos conjuntos é:
A–B= 
►Complementar
B  C = { } ou B  C =  Dados dois conjuntos A e B em que A  B, chamamos
de complementar de A em B
então B e C são conjuntos distintos.
, o conjunto formado pelos elementos de que pertencem a
B que não pertencem a A
►Diferença entre dois conjuntos.
AB  = B - A
Dados dois conjuntos A e B chama-se conjunto diferença ou
diferença entre A e B o conjunto formado pelos elementos
de A que não pertencem a B.
O conjunto diferença é representado por A - B
Resumo teórico 5

6. Pré-vestibulinho
Matemática
► Número de elementos da união de
Exemplo 1:
A = { 1, 2 , 3} e B = { 1, 2, 3, 4, 5} então = B – A = { 4, conjuntos
5}
Sendo n(A) o número de elementos do conjunto A e
n(B) o número de elementos do conjunto B, temos:
n ( A  B ) = n (A) + n(B) – n(A  B )
Exemplo1:
n(A) = 5
Exercícios resolvidos
n (B) = 5
1. Se A = { 1, 2, 3, 4 , 5} e B = { 2, 3, 7} e C = { 2, 4, 6} ,
determine: n(A  B ) = 2
a) A  B
A  B = { 1, 2, 3, 4 , 5}  { 2, 3, 7} = { 1, 2, 3, 4 , 5, 7} Sendo n ( A  B ) = n (A) + n(B) – n(A  B ), então
n ( A  B ) = 5 + 5 – 2. Logo n ( A  B ) = 8
b) A  B
A B = { 1, 2, 3, 4 , 5}  { 2, 3, 7} = { 2, 3}
c) ( A  B )  ( B C)
Exemplo2:
A  B = { 1, 2, 3, 4 , 5, 7}
B  C = { 2, 3, 7 }
n(A) = 3
(A B)  (B C) n (B) = 4
{ 1, 2, 3, 4 , 5, 7}  { 2, 3, 7 } = { 2, 3, 4, 7 }
n(A  B ) = 
2. Se A = { 1, 2, 3, 4 , 5 }, B = { 2, 3, 6} e C = { 1, 2, 4 },
encontre:
Sendo n ( A  B ) = n (A) + n(B) – n(A  B ), então
a) B – C
B – C = { 2, 3, 6 } – { 1, 2, 4 } = { 3, 6 }
b)
Exercícios resolvidos
A - C = { 1, 2, 3, 4 , 5} - { 1, 2, 4 } = { 3, 5 }
1. Determine n (D  M ) sendo D = { 1, 2, 3, 4, 6, 8, 12, 24}
e M = { 3, 6, 9, 12, 15, 18, 21, 24 }
Resumo teórico 6

7. Pré-vestibulinho
Matemática
n(D) = 8
n (M) = 8
n(A  B ) = 4
Sendo n ( A  B ) = n (A) + n(B) – n(A  B ), então
n ( A  B ) = 8 + 8 – 4. Logo n ( A  B ) = 12
2. Em uma universidade, 80% dos alunos lêem o jornal A e
60% o jornal B. Sabendo que todo aluno lê pelo menos um
dos jornais, qual o percentual de alunos que lêem ambos
os jornais?
Solução
Como todos os alunos lêem pelo menos um jornal,
n ( A  B )= 100% . Então:
n ( A  B ) = n (A) + n(B) – n(A  B)
100% = 80% + 60% – n(A  B)
n(A  B) = 140% - 100%
n(A  B) = 40%
Resumo teórico 7

8. Pré-vestibulinho
Matemática
a
2. NÚMEROS NATURAIS, INTEIROS, = x |x = , a ; b e b≠0
b
RACIONAIS E IRRACIONAIS.
10 6
Inteiro: - 10, − , + 6, +
1 1
2.1.Conjunto dos Números Naturais ( )
1 132
Decimal exato: 0,1 ; ; 1,32 =
= { 0,1,2,3,4,.. } 10 100
*= { 0,1,2,3,4,.. } Dízima periódica:
7
a) 0,777... =
O conjunto dos números é fechado em relação as 9
operações de adição e multiplicação; isto é a adição de
dois números naturais é um outro número natural e a 6 2
b) 1,666 ... = 1 + 0,666... = 0,666... = =
multiplicação de dois números naturais terá como 9 3
resultado também um número natural. 2 3+2 5
1+ = =
3 3 3
Representação geométrica dos números naturais
36− 3 33 11
c) 0, 366... = = =
90 90 30
Cuidado! : Nem todo número racional é inteiro.
𝟏
Ex.: 𝟐
= 0,5 é racional mas não é inteiro!
2.2. Números inteiros ( )
= { ..., -3, -2, -1, 0, 1, 2 , 3, ...}
2.4. Conjunto dos Números Irracionais ( I )
Subconjuntos de
Os números irracionais apresentam infinitas casas
* = { ..., -3, -2, -1, 1, 2, 3, ... } decimais e não periódicas, são números que não podem ser
escritos na forma de uma fração.
+ = { 0, 1, 2, 3, ... }
Exs: , 2 , 3 ,  , etc...
*+ = { 0, 1, 2, 3, ... }
Obs.: As raízes quadradas de números que não são
- = { ..., -4, -3, -2, -1, 0 } quadrados perfeitos são também chamadas de números
irracionais.
*- = { ..., -4, -3, -2, -1 }
Representação geométrica dos números inteiros
2.5. Números Reais ( )
A união dos conjuntos dos números racionais e
irracionais chama-se conjunto dos números, que será
indicado por ” ”
2.3. Conjunto dos Números Racionais ( )
= { números racionais}  { números irracionais }
Todo número que pode ser escrito na forma de fração
Resumo teórico 8

9. Pré-vestibulinho
Matemática
momento, a letra relativa à posição da cadeira ocupada por
Bruna é
(A) D.
(B) I.
(C) K.
(D) P.
Exercícios
1.(SENAI 2008) Num jantar de comemoração, no final do
ano passado, todos os participantes resolveram pedir o
mesmo prato e a mesma sobremesa. No final do jantar
pagaram um total de R$ 450,00 pelo prato principal e R$
250,00 pela sobremesa. Se cada sobremesa custou R$ 5,00
a menos do que o prato principal, então o grupo era
formado por
a. 20 pessoas.
b. 30 pessoas.
c. 40 pessoas.
d. 50 pessoas. (E) R.
e. 60 pessoas.
3.(Trajano 2007) Quando estava lendo uma reportagem
sobre a sua banda favorita, Paula observou que havia um
2.(Trajano 2007) A roda-gigante de um parque de diversões borrão de tinta no texto, como é mostrado a seguir:
tem dezoito cadeiras, igualmente espaçadas ao longo do
seu perímetro e move-se no sentido anti-horário, isto é, no Curiosa, Paula determinou que o número de ingressos
sentido contrário ao dos ponteiros do relógio. oferecidos para a área vip foi
(A) 260.
(B) 400.
(C) 540.
(D) 760.
(E) 910.
4.(Trajano 2007) Uma equipe de reportagem parte em um
carro em direção a Santos, para cobrir o evento “Música
Boa Só na Praia”. Partindo da cidade de São Paulo, o veículo
deslocou-se com uma velocidade constante de 54 km/h,
durante 1 hora. Parou em um mirante, por 30 minutos, para
gravar imagens da serra e do movimento de automóveis. A
seguir, continuaram a viagem para local do evento, com o
veículo deslocando-se a uma velocidade constante de 36
km/h durante mais 30 minutos. A velocidade escalar média
durante todo o percurso foi, em m/s,
de:................................
Na figura, as letras A, B, C, ... e R indicam as posições em
que as cadeiras ficam cada vez que a roda-gigante pára. (A) 10 m/s. (D) 36 m/s.
Com a roda-gigante parada, Bruna senta-se na cadeira que (B) 12 m/s. (E) 42 m/s.
está na posição A, posição mais baixa da roda-gigante. A (C) 25 m/s.
roda-gigante move-se de uma volta e pára. Nesse
Resumo teórico 9

10. Pré-vestibulinho
Matemática
5.(Trajano 2007) Eduardo e Mônica estavam brincando de adivinhações com números inteiros positivos.
Ao ouvir a resposta de Mônica, Eduardo imediatamente revelou o número original que Mônica havia pensado.
O número que Mônica havia pensado era um
(A) divisor de 12.
(B) divisor de 15.
(C) divisor de 24.
(D) múltiplo de 5.
(E) múltiplo de 12.
Resumo teórico 10

11. Pré-vestibulinho
Matemática
6.(Cotil 2002) As infrações de transito são classificadas de
acordo com o quadro ao lado. Se um condutor de Qual o total de pontos do lutador japonês e do coreano,
automóvel cometer as seguintes infrações: uma grave, duas respectivamente?
medias e 1 leve, quantos pontos seriam registrados na sua
carteira de motorista? E qual seria o valor total pago dessas 1 9
a) e
multas em reais? 1 UFIR = R$ 1,0641 fonte: Receita 2 8
Federal
10 5
b) e
8 8
Infrações Pontos Multa
4 7
Gravíssima 7 180 UFIRs c) e
8 8
Grave 5 120 UFIRs 2 5
d) e
8 8
Média 4 80 UFIRs
4 5
Leve 3 50 UFIRs e) e
8 8
↘ PROBLEMAS COM FRAÇÕES
8.(Cotil 2006) No COTIL , a alunos carentes são oferecidas
6.(Cotil 2005) O medo de atentado terrorista forçou a bolsa-trabalho, cujo valor varia a cada ano. Depois de uma
idealização de um plano de segurança para os jogos rigorosa avaliação, alguns alunos são beneficiados e
Olímpicos de 2004 de Atenas. A segurança reforçada contou prestam serviço à escola em horário oposto ao que
5 1
com milhares de homens e mulheres, sendo policiais , estudam. Em um determinado ano, um estudante recebeu
9 3 uma bolsa. Descubra quanto recebeu, sabendo que no final
militares , segurança particulares e voluntários e outros 5 4
mil homens eram da guarda costeira. O total de homens do mês ele gastou do total e, em seguida, enviou mais
5
que participaram da segurança em Atenas 2004 foi de : 1
, restando-lhe..apenas..R$.7,00.
a) 15 mil 6
b) 25 mil
c) 30 mil a) R$ 150,00 d) R$ 240,00
d) 45 mil b) R$ 180,00 e) R$ 270,00
e) 50 mil c) R$ 210,00
7.(Cotil 2005) O judô olímpico é um dos esportes mais
premiados do Brasil. O primeiro judoca brasileiro a 9.(Cotil 2006) As epidemias que afetam os animanis
conquistar o ouro foi Aurélio Miguel, em 1998. Para quem preocupam não só o Brasil, como também a humanidade.
na pratica o esporte, entender aquele empurra-empurra, Um fazendeiro da região Centro-Oeste do Brasil possuía um
agarra-aguarra e golpes rápidos não é muito fácil. Para rebanho de gado para corte e, num certo mês do ano, viu
compreender um pouco mais da dinâmica desse esporte, seu rebanho ser dizimado por uma dessas epidemias. Na
1
um caminho é aprender a matemática que envolve o primeira semana perdeu do rebanho; na segunda
sistema de pontuação dos golpes, conforme a tabela 3
1 1 1
abaixo: semana, perdeu ; na terceira ; na quarta ,
6 9 12
sobrando apenas 792 cabeças de gado. Quantas cabeças do
Golpe Valor Punição Valor rebanho ele perdeu?
Ippon 1 ponto Shidô 1/8 ponto
Waza-ari 1/2 ponto Chui 1/4 ponto
Yuko 1/4 ponto Keikoku 1/2 ponto 10.(Cotil 2007) Os desertos avançam. O total de áreas
Koka 1/8 ponto Hansoku-make 1 ponto atingidas por seca dobrou em trinta anos. Só na China, as
áreas desérticas avançaram 10.000 quilômetros quadrados
Acompanhe a descrição de uma luta entre um japonês e um por ano, o equivalente ao território do Líbano. A Área total
2
coreano. da Terra é de aproximadamente 510 milhões de km . Sabe-
3 1
se que da superfície da Terra são cobertos por água e
4 3
 O lutador japonês obteve: um koka, um yoko, um waza- do restante é coberto por desertos. A área dos desertos, em
ari e três shidô milhões de quilômetros quadrados corresponde a
aproximadamente:
 O coreano teve o seguinte desempenho: um waza-ari, dois
koka, um Chuí,um shidô e um yoko.
Resumo teórico 11

12. Pré-vestibulinho
Matemática
O aluno B errou, pois dividiu as barras em 5 partes iguais,
a) 127,5 5
logo sua resposta deveria ser .
b) 170 4
c) 42,5
d) 420,5 d) O aluno A acertou, respondendo com uma adição de
e) 425 frações cuja soma corresponde à resposta correta.
O aluno B errou, pois dividiu as barras em 5 partes iguais,
5
logo a resposta deveria ser .
11.(PSS-SEE/SP) Um professor de uma escola de música vai 4
comprar um livro para cada um dos 270 alunos.
Pesquisando
preços na internet, encontrou o seguinte: e) O aluno A acertou, pois dividiu as quatro barras em 4
• No site A, o preço de cada livro era R$ 16,75. partes iguais e dividiu o que sobrou aos seus 5
• No site B, o preço de cada livro era R$ 25,00, e na compra amigos. O aluno B errou, pois dividiu as barras em 5 partes
de dois livros o terceiro era cortesia. 5
iguais, logo sua resposta deveria ser .
4
Qual a melhor opção para o professor?
a) O site A, pois economizaria R$ 2.227,50 em relação ao
que pagaria no site B. 12.(PSS-SEE/SP) A partir de um valor inicial igual a 16000,
b) O site A, pois economizaria R$ 1.215,00 em relação ao certa população P1 de bactérias dobra a cada 30 minutos.
que pagaria no site B. Simultaneamente, partindo de um valor inicial 8 vezes
c) O site B, pois economizaria R$ 225,50 em relação ao que menor, outra população P2 de bactérias cresce,
pagaria no site A. dobrando de valor a cada 15 minutos. Em qual instante t as
d) O site B, pois economizaria R$ 22,50 em relação ao que duas populações terão o mesmo valor?
pagaria no site A. a) 60 minutos.
e) O site B, pois economizaria R$ 2,25 em relação ao que b) 90 minutos.
pagaria no site A. c) 120 minutos.
3.(PSS-SEE/SP) Um professor de Matemática apresentou o d) 150 minutos.
seguinte problema aos seus alunos: e) 180 minutos.
“Roberto comprou quatro barras de chocolate e dividiu
igualmente aos seus cinco amigos. Qual a fração da barra
que cada um receberá?”
Dois alunos responderam da seguinte maneira à questão do
professor:
3 1
Aluno A: Cada um receberá +
4 20
4
Aluno B: Cada um receberá a fração
5
Considerando as resoluções dos alunos, assinale a
alternativa correta:
a) O aluno A acertou, pois dividiu as quatro barras em 4
partes iguais e dividiu o que sobrou aos seus 5 amigos. O
aluno B também acertou, pois dividiu as barras em 5 partes
4
iguais, representando
5
b) O aluno A errou, respondendo com uma adição de
frações cuja soma não corresponde à resposta correta.
O aluno B acertou, pois dividiu as barras em 5 partes iguais,
4
representando
5
c) O aluno A errou, respondendo com uma adição de
frações cuja soma não corresponde à resposta correta.
Resumo teórico 12

13. Pré-vestibulinho
Matemática
3.2.1. Propriedades da Radiciação
3. POTENCIAÇÃO E RADICIAÇÃO
3.1. Potenciação Para a  ,b  ,n  *, m  *, temos:
Para a   ,n
n n n
,b 1) a · b = a · b
n
a n a
2) n = ,b≠0
b b
n m m. n
Assim; 3) a = a
 a0 = 1
4) ( a )p = p
n
, *
 a1 = a
5)
 an = a · a · ... · a , se n  2
n fatores Obs.: Para radicais de índice par, devemos ter b  0 e a 
0
 a-n = = a≠0 3.2.2. Potenciação com expoente racional
Sendo p  , n *, temos:
3.1.1. Propriedades da Potenciação
a +  a =
1) a
m
· n
a =a
m+n
p
m
2) a : a = a
n m-n
0 = 0 , para > 0
n
a= 0
m n
3) (a ) = a
m
·n p
0 não é definido para ≤ 0
n
4) (a · m
b) = a
m
·bm
a nem sempre é real se n for par
m m m
5) (a : b) = a : b , b ≠0
a - 
a = se n for ímpar
3.2. Radiciação
Para a    Todas as propriedades da potenciação com expoente inteiro são
,b ,n * , temos:
válidas também para a potenciação com expoente racional.
Assim,
 b = an
n
b =a
Resumo teórico 13

14. Pré-vestibulinho
Matemática
4. EXPRESSÕES ALGÉBRICAS
Esses termos semelhantes podem ser reduzidos, basta
São expressões matemáticas que apresentam letras ou
conservar a parte literal e fazer as respectivas operações
apenas letras, as quais são chamadas de variáveis ou
com os coeficientes numéricos. Voltando ao exemplo
incógnitas.
anterior temos:
2 2
2 3
( 3 xy + 6 xy ) e ( - 2 abc + 10 abc ), reduzindo esses
Ex.: 2a b + 3xy – 7a2x3 – 7a2x2 – b2 y2 2
termos temos: 9xy + 8abc
No exemplo acima:
 2; 3; -7 e -1 são chamados de coeficientes numéricos
4.3. Polinômio
Toda expressão racional e inteira é determinada pelo
 a b ; xy ; a x ; a x e b y são chamadas de parte
2 3 2 3 2 2 2 2
número de termos da expressão algébrica.
literal
a) Monômio: polinômio que possui apenas um termo
2a2b + 3xy3 – 7a2x3 – 7a2x2 – b2 y2 2 4
Ex.: 2 x y z
1º termo 2º termo 3º termo 4º termo 5º termo
b) Binômio: polinômio que possui dois termos
Os termos são separados apenas por adição ou subtração. 2 4
Ex.: 3 x y + 2ab
2
c) Trinômio: polinômio que possui três termos
4.1. Classificação das expressões algébricas 2 4 2 3
Ex.: 5 a y + 7xb – 7xy z
a) Racional : Quando não existe variável dentro de uma  Acima de três termos, todos os demais são chamados de
raiz, esses tipos de expressões se subdividem em: Polinômio.
 Inteiras: quando não aparecem variáveis no Cuidado!: Só podemos classificar um polinômio após
denominador reduzirmos todos os termos semelhantes.
2 4
Exs.: 3x + 1 ; 7xy – by 2 2 2
Por exemplo: 4x + 3ab + 4x y – 5x aparentemente é um
2 2
polinômio porém o primeiro e o quarto termo ( 4x e – 5x )
 Fracionárias: quando aparecem variáveis no são semelhantes, podendo ser reduzidos. Após a redução
denominador observamos que o polinômio é um trinômio com esse
2 3 5 2
Exs.: + 5x -2 ; +c aspecto:
x ab
-x2 + 3ab + 4x2y
b) Irracional : Quando existe variável dentro de uma raiz.
2 3
4.4. Grau do Polinômio
Exs.: 3 3x + 5a b ; 2abc – y
O grau de termos é a soma dos expoentes de
suas variáveis, o termo que possuir maior soma de
expoentes determinará o grau do polinômio.
4.2. Termos semelhantes 2 4 2
Ex.: 3a b – 7b + 3 x y z
3 2
Termos que apresentam a mesma parte literal, inclusive os 2 3
1º Termo : 3 a b = 2 + 3 = 5 ( Quinto grau)
expoentes das variáveis. 2
2º Termo : -7 b = 2 ( Segundo grau)
3 2
3º Termo : 3 x y z = 3 + 2 + 1 = 6 ( Sexto grau) <maior>
2 2
Ex.: 3 xy - 2 abc + 6 xy + 10 abc
Podemos observar que esse trinômio é do sexto grau
Termos semelhantes
Resumo teórico 14

15. Pré-vestibulinho
Matemática
4.5. Valor numérico de uma expressão
Toda expressão algébrica tem o seu valor numérico, esse
valor é encontrado a partir do momento em que temos
ou atribuímos valores para as letras. Se em um exercício é
pedido para que calcule o valor numérico da expressão
2
algébrica 2x y é preciso que saibamos ou atribuímos valores
para as letras x e y.
2
Então vamos supor que na equação 2x y, os valores das
letras seja x = -2 e y = 1, agora substituindo esses valores,
chegaremos em um valor numérico.
2
2x y
2 · (-2) ·1
2
2·4·1 =8
 Valor numérico da expressão 2x y
2
Veja mais um exemplo de como achar o valor numérico da
expressão a + ab + 5. O valor numérico desse e de todas as
expressões algébricas irão variar dependendo do valor que
iremos atribuir para as letras.
Nesse exemplo vamos supor que as letras a = 5 e b = -5.
5 + 5 · (-5) + 5
5 – 25 + 5
-20 + 5 = - 15
 Valor numérico da expressão a + ab + 5
Resumo teórico 15

16. Pré-vestibulinho
Matemática
5. PRODUTOS NOTÁVEIS E FATORAÇÃO 5º Caso: Trinômio do 2º grau
2
São expressões da forma x - Sx + P, em que S e P
repre-sentam, respectivamente, a soma e o produto de
dois núme-ros a e b tal que se pode escrever:
5.1. Produtos notáveis
São produtos que aparecem com muita freqüência x2 - Sx + P = ( x –(x1 )) ( x + (x2))
na resolução de equações ou no desenvolvimento de Exs.:
2
expressões. a) x + 7x + 12 = ( x+3) (x+4)
Vejamos alguns casos: S P
2
2 2 2 2 2 b) x -6x +8 = ( x - 2 ) (x - 4)
a) (a + b) = ( a+ b)( a+b ) = a + ab + ba + b = a + 2ab + b
S P
2 2 2 2 2
b) (a - b) = ( a - b)( a – b ) = a - ab - ba + b = a - 2ab + b 2
c) x +2x -8 = ( x - 2 ) (x + 4)
S P
2 2 2 2
c) ( a +b )( a – b ) = a – ab + ba – b = a - b
Resumindo:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
( a +b )( a – b ) = a2 - b2
5.2. Fatoração
Fatorar uma expressão algébrica é transformá-la em
produto. Vejamos alguns casos.
1º Caso: Fator comum em evidência
2 3 4 2 2
Ex.: 6x + 12x z – 8 x b = 2x (3 + 6xz – 4x b )
2º Caso: Agrupamento
Ex.: xy + xz + ay + az = x( y + z ) + a (y + z ) = (y + z) ( x + a )
3º Caso: Diferença de dois quadrados
2 2
Ex.: x – y = ( x + y ) ( x – y )
4º Caso: Trinômio quadrado perfeito
Exs.:
2 2 2
a) x +2xy + y = ( x + y )
x 2 y = 2xy
2 2 2
b) x -2xy + y = ( x - y )
x -2 y = -2xy
Resumo teórico 16

17. Pré-vestibulinho
Matemática
6. RAZÕES E PROPORÇÕES 𝐚 𝐜
=  ax d = bxc
𝐛 𝐝
6.1. Razão
Obs. A recíproca também é verdadeira
Razão é a comparação entre grandezas de mesma
a c
espécie. Essa comparação é representada por uma a· d = b·c  =
fração, onde o numerador é chamado de antecedente e o b d
denominador de conseqüente.
Exs.:
Exs.:
3 a) Calcule o valor de “x”.
a) A razão entre 3 e 7 = ,
7
(onde 3 é antecedente e 7 conseqüente) x 10
= = x · 4 = 2 · 10
2 4
7 4x = 20
Se invertermos , a razão entre 7 e 3 será , x=5
3
(agora 7 é antecedente e 3 conseqüente)
2 1 b) Calcule o valor de “y”.
b) A razão entre 4 e 2 = 2, a razão entre 2 e 4 = =
4 2
9 y
3 8 2 8 27
= = 2 · y = 9 · 0,2
2 0,2
c) A razão entre e = : = 2y = 1,8
2 9 3 9 16
y = 0,9
6.2. Proporção 6.3. Números proporcionais
Duas seqüências de números são proporcionais
É uma igualdade entre duas razões.
quando a razão entre dois números correspondentes de
cada uma das seqüências for sempre a mesma.
Exs.:
Os números proporcionais são divididos em 2 grupos:
A proporção a seguir pode ser representada da seguinte
os diretamente proporcionais e os inversamente
maneira:
proporcionais. Há também um outro grupo que não
pertence a esses chamados números não proporcionais.
6.3.1. Números diretamente proporcionais
Dada uma seqüência
a; b; c; d; ... e a’; b’ ; c’ ; d’; ... então:
Lê-se: 3 está para 2 assim como 9 está para 6 a b c d
Nesta proporção, o 3 e 6 são extremos e o 2 e o 9 são = = = = .... = k onde
a´ b´ c´ d´
meios.
k = constante de proporcionalidade
5.2.1. Propriedade fundamental das proporções
Ex: Considere as seqüências
2; 4; 8; 16; 32 e 3; 6; 12; 24; 48
“O produto dos meios é igual ao produto dos extremos”
2 4 8 16 32 𝟐
3 6 = = = = =
Ex.: =  2· 6 = 3·4 3 6 12 24 48 𝟑
2 4
= 12
2
é a constante de proporcionalidade.
Generalizando: 3
Resumo teórico 17

18. Pré-vestibulinho
Matemática
Portanto, podemos afirmar que as duas seqüências 3.(Trajano 2008)
são diretamente proporcionais devido apresentarem
sempre como resultado a razão entre as grandezas
𝟐
relacionadas
𝟑
6.3.2. Números inversamente proporcionais
Dada uma seqüência
a; b; c; d; ... e a’; b’ ; c’ ; d’; ... então:
a b c d
1 = 1 = 1 = 1 = .... = k onde
a´ b´ c´ d´
a · a´ = b · b´ = c · c´ = d · d´ = .... = k
Ex.: Considere as seqüências 2; 4; 8; 16; 32 e 48; 24; 12; 6;
3
2 4 8 16 32
1 = 1 = 1 = 1 = 1 = .... = k onde
48 24 12 6 3
Se o temor de Eva, a personagem da cena apresentada, se
2 · 48 = 4 · 24 = 8 · 12 = 16 · 6 = 32· 3 = 96
confirmar, e os três dias de espera forem venusianos, então
96 é a constante de proporcionalidade. na Terra terão se passado (Obs. Desconsidere o ano bissexto)
Portanto, podemos afirmar que as duas seqüências são
inversamente proporcionais. (A) 1 ano, 10 meses e 19 dias.
(B) 1 ano, 11 meses e 29 dias.
(C) 2 anos e 2 dias.
Exercícios (D) 2 anos e 5 dias.
(E) 2 anos e 9 dias.
1.(SENAI) Dos 1.200 funcionários de uma empresa, 60% têm
idade superior a 30 anos. Se entre o número de homens e o
de mulheres com idade superior a 30 anos a razão é de 3
homens para 2 mulheres, pode-se afirmar que a quantidade
de mulheres com idade superior a 30 anos nessa empresa é 4.(PSS-SEE/SP) O gráfico abaixo indica o preço em reais de
cada bolsa que uma fábrica produz, de acordo com o
a. 288.
b. 296. número de bolsas compradas pelas lojas.
c. 312.
d. 360.
e. 374.
2. (Trajano 2008) É possível combater o vibrião colérico
com o uso de uma solução aquosa de hipoclorito de sódio
(NaClO) a uma concentração mínima de 0,11g/L. A massa de
hipoclorito de sódio necessária para se preparar 10 litros
dessa solução, expressa em miligramas, é
(A) 0,11.
(B) 1,10.
(C) 110.
(D) 1 100.
(E) 11 000.
Resumo teórico 18

19. Pré-vestibulinho
Matemática
Considere as afirmações abaixo:
I. As grandezas envolvidas são diretamente proporcionais.
II. As grandezas envolvidas são inversamente proporcionais.
III. As grandezas não são nem diretamente e nem
inversamente proporcionais.
IV. Analisando a relação existente entre as grandezas
envolvidas, percebemos que, quando há aumento de
uma, ocorre uma diminuição da outra.
Dentre essas afirmações:
a) Apenas a I está correta.
b) Apenas a II está correta.
c) Apenas a III está correta.
d) I e IV estão corretas.
e) III e o IV estão corretas.
Resumo teórico 19

20. Pré-vestibulinho
Matemática
7. REGRA DE TRÊS Velocidade
(Km/h)
Tempo (h)
400 3
7.1. REGRA DE TRÊS SIMPLES 480 x
Regra de três simples é um processo prático para resolver Identificação do tipo de relação:
problemas que envolvam quatro valores dos quais conhecemos
três deles. Devemos, portanto, determinar um valor a partir dos
três já conhecidos.
Passos utilizados numa regra de três simples:
1º) Construir uma tabela, agrupando as grandezas da mesma Inicialmente colocamos uma seta para baixo na coluna que
espécie em colunas e mantendo na mesma linha as grandezas de contém o x (2ª coluna).
espécies diferentes em correspondência. Observe que: Aumentando a velocidade, o tempo do percurso
diminui.
2º) Identificar se as grandezas são diretamente ou Como as palavras são contrárias (aumentando - diminui),
inversamente proporcionais. podemos afirmar que as grandezas são inversamente
proporcionais. Assim sendo, colocamos uma outra seta no sentido
3º) Montar a proporção e resolver a equação. contrário (para cima) na 1ª coluna. Montando a proporção e
resolvendo a equação temos:
Exemplos:
2
1) Com uma área de absorção de raios solares de 1,2m , uma
lancha com motor movido a energia solar consegue produzir 400
2
watts por hora de energia. Aumentando-se essa área para 1,5m ,
qual será a energia produzida?
Solução: montando a tabela:
2
Área (m ) Energia (Wh)
1,2 400
1,5 x
Logo, o tempo desse percurso seria de 2,5 horas ou 2 horas e 30
Identificação do tipo de relação: minutos.
3) Bianca comprou 3 camisetas e pagou R$120,00. Quanto ela
pagaria se comprasse 5 camisetas do mesmo tipo e preço?
Inicialmente colocamos uma seta para baixo na coluna que Solução: montando a tabela:
contém o x (2ª coluna).
Observe que: Aumentando a área de absorção, a energia solar Camisetas Preço (R$)
aumenta. 3 120
Como as palavras correspondem (aumentando - aumenta), 5 x
podemos afirmar que as grandezas são diretamente
proporcionais. Assim sendo, colocamos uma outra seta no mesmo Observe que: Aumentando o número de camisetas, o preço
sentido (para baixo) na 1ª coluna. Montando a proporção e aumenta.
resolvendo a equação temos: Como as palavras correspondem (aumentando - aumenta),
podemos afirmar que as grandezas são diretamente
proporcionais. Montando a proporção e resolvendo a equação
temos:
Logo, a energia produzida será de 500 watts por hora.
Logo, a Bianca pagaria R$ 200,00 pelas 5 camisetas.
2) Um trem, deslocando-se a uma velocidade média de
400Km/h, faz um determinado percurso em 3 horas. Em quanto
tempo faria esse mesmo percurso, se a velocidade utilizada fosse 4) Uma equipe de operários, trabalhando 8 horas por dia,
de 480km/h? realizou determinada obra em 20 dias. Se o número de horas de
serviço for reduzido para 5 horas, em que prazo essa equipe fará o
Solução: montando a tabela:
mesmo trabalho?
Resumo teórico 20

21. Pré-vestibulinho
Matemática
Solução: montando a tabela: proporcional (seta para baixo na 3ª coluna). Devemos
igualar a razão que contém o termo x com o produto das
Horas por Prazo para término
outras razões de acordo com o sentido das setas.
dia (dias)
8 20 Montando a proporção e resolvendo a equação temos:
5 x
Observe que: Diminuindo o número de horas trabalhadas por
dia, o prazo para término aumenta.
Como as palavras são contrárias (diminuindo - aumenta),
podemos afirmar que as grandezas são inversamente
proporcionais. Montando a proporção e resolvendo a equação
temos:
Logo, serão necessários 25 caminhões.
2) Numa fábrica de brinquedos, 8 homens montam 20
carrinhos em 5 dias. Quantos carrinhos serão montados por
7.2. REGRA DE TRÊS COMPOSTA 4 homens em 16 dias?
Solução: montando a tabela:
A regra de três composta é utilizada em problemas com Homens Carrinhos Dias
mais de duas grandezas, direta ou inversamente 8 20 5
proporcionais. 4 x 16
Exemplos: Observe que:
1) Em 8 horas, 20 caminhões descarregam 160m de
3 Aumentando o número de homens, a produção de
areia. Em 5 horas, quantos caminhões serão necessários carrinhos aumenta. Portanto a relação é diretamente
para descarregar 125m ?
3 proporcional (não precisamos inverter a razão).
Solução: montando a tabela, colocando em cada coluna Aumentando o número de dias, a produção de
as grandezas de mesma espécie e, em cada linha, as carrinhos aumenta. Portanto a relação também é
grandezas de espécies diferentes que se correspondem: diretamente proporcional (não precisamos inverter a razão).
Devemos igualar a razão que contém o termo x com o
Horas Caminhões Volume produto das outras razões.
8 20 160 Montando a proporção e resolvendo a equação temos:
5 x 125
Identificação dos tipos de relação:
Inicialmente colocamos uma seta para baixo na coluna
que contém o x (2ª coluna).
Logo, serão montados 32 carrinhos.
A seguir, devemos comparar cada grandeza com aquela
onde está o x.
Observe que: 3) Dois pedreiros levam 9 dias para construir um muro
Aumentando o número de horas de trabalho, podemos com 2m de altura. Trabalhando 3 pedreiros e aumentando a
diminuir o número de caminhões. Portanto a relação é altura para 4m, qual será o tempo necessário para
inversamente proporcional (seta para cima na 1ª coluna). completar esse muro?
Aumentando o volume de areia, devemos aumentar o Inicialmente colocamos uma seta para baixo na coluna
número de caminhões. Portanto a relação é diretamente que contém o x. Depois colocam-se flechas concordantes
Resumo teórico 21

22. Pré-vestibulinho
Matemática
para as grandezas diretamente proporcionais com a
incógnita e discordantes para as inversamente
proporcionais, como mostra a figura abaixo:
Montando a proporção e resolvendo a equação temos:
Logo, para completar o muro serão necessários 12 dias.
Exercícios complementares
Agora chegou a sua vez de tentar. Pratique tentando
fazer esses exercícios:
1) Três torneiras enchem uma piscina em 10 horas.
Quantas horas levarão 10 torneiras para encher 2 piscinas?
Resposta: 6 horas.
2) Uma equipe composta de 15 homens extrai, em 30
dias, 3,6 toneladas de carvão. Se for aumentada para 20
homens, em quantos dias conseguirão extrair 5,6 toneladas
de carvão? Resposta: 35 dias.
3) Vinte operários, trabalhando 8 horas por dia, gastam
18 dias para construir um muro de 300m. Quanto tempo
levará uma turma de 16 operários, trabalhando 9 horas por
dia, para construir um muro de 225m? Resposta: 15 dias.
4) Um caminhoneiro entrega uma carga em um mês,
viajando 8 horas por dia, a uma velocidade média de 50
km/h. Quantas horas por dia ele deveria viajar para
entregar essa carga em 20 dias, a uma velocidade média de
60 km/h? Resposta: 10 horas por dia.
5) Com uma certa quantidade de fio, uma fábrica produz
5400m de tecido com 90cm de largura em 50 minutos.
Quantos metros de tecido, com 1 metro e 20 centímetros de
largura, seriam produzidos em 25 minutos? Resposta: 2025
metros.
Resumo teórico 22

23. Pré-vestibulinho
Matemática
E porque ter noção desta distinção?? Ela se torna
8. PORCENTAGEM E PROBLEMAS DE muito importante na resolução de problemas envolvendo
...APLICAÇÃO. dinheiro.
Porcentagem é uma razão centesimal, ou seja, o
denominador é igual a 100.
8.1.1. Porcentagem sobre o preço de custo
25
Ex.: que se indica por 25%
100 Quando o cálculo sobre o preço de lucro (ou prejuízo) é
calculado, em bases percentuais, em cima do preço de
Existem dois métodos para se calcular porcentagem:
custo do produto adquirido, temos o que é chamado de
porcentagem sobre o custo. Este é o processo normal, e que
a) Fração de um valor: Multiplica-se a fração pelo valor. é usado e adotado no mercado comercial.....................
Ex: Calcule 20% de 45 Desta forma, se um comerciante ou pessoa física,
compra um determinado produto por um valor de R$
20 900 200,00 (preço de custo) e este for ser revendido com um
· 45 = =9
lucro de 30%, isto quer dizer que nesta operação o lucro em
100 100
espécie da operação é de R$ 30,00 (lucro) para cada valor
Portanto 20% de 45 é igual a 9 de R$ 100,00 do preço do custo.
b) Regra de Três Simples e direta: Comparação entre duas
grandezas diretamente proporcionais
Acompanhe o raciocínio:
Ex: Calcule 30% de 70
Custo Lucro
Estamos comparando porcentagem e valor. 70 é o valor R$ 100,00 R$ 30,00
total portanto equivale a 100%.
R$ 100,00 R$ 30,00
Custo total = R$ 200,00 Lucro total = R$ 60,00
100 % ............ 70
20% ................ x 100· x = 20 ·70
100 x = 1400
Através de um cálculo da regra de três , temos:
1400
x = R$ 200,00 .............. 100%
100
X .................... 30%
x = 14 200 x 30
X=
100
Obs.: É mais conveniente resolver por regra de três, pois
serve para todos os casos. 6000
X =
100
8.1. PROBLEMAS DE APLICAÇÃO – LUCROS E
......PREJUÍZOS X = R$ 60,00 (valor do lucro total na
operação)
Todo comerciante compra uma certa mercadoria
por um determinado preço, que é chamado de preço de Em toda operação, envolvendo problemas
custo, e em seguida, efetua a revenda do mesmo com lucro relacionados com porcentagem sobre o custo do produto,
ou prejuízo, dependendo do preço que a mercadoria foi as partes obrigatórios de cálculos na operação são:
passada ao mercado consumidor.
Em problemas envolvendo porcentagem sobre compra » Venda
e venda de mercadorias, temos os seguintes casos » Custo
distintos: » Lucro (ou prejuízo, conforme operação)
» porcentagem (%) sobre venda Para que haja uma memorização melhor sobre
» porcentagem (%) sobre custo estes elementos fundamentais de cálculo sobre
porcentagem de custo, observe:
Resumo teórico 23

24. Pré-vestibulinho
Matemática
C = CUSTO C*L=V » 100% + 50% = 150%
V = VENDA R$ 300,00 .............. 100% (custo da operação)
X ...................... 150% (venda da operação)
L = LUCRO
150 x 300
X=
P = PREJUÍZO 100
45000
X= = R$ 450,00
100
Dicas importantes!
Resposta:O valor do produto será de R$ 450,00
1. O preço de custo (ou preço de compra) é sempre igual a
100% (cem por cento)
c) Uma pessoa vendeu um automóvel pelo valor de
R$ 25.000,00, ganhando o valor de 20% (vinte por cento)
2. A venda do produto (com prejuízo na operação) é sobre o custo. Qual foi o lucro desta pessoa nesta
sempre igual ao preço de custo menos o prejuízo, da operação?
seguinte forma:
Solução:
C–P=V ou V=C–P
100% - 30% = 70% 70% = 100% - 30%
C + L = V » 100% + 20% = 120%
3. a venda do produto (com lucro na operação) é sempre 25.000 ................. 120% (venda da operação)
igual à soma do custo mais o lucro, da seguinte forma: X .................... 20% (lucro da operação)
C+L=V ou V=C+L 25000 x 20
100% + 30% = 130% 130% = 100% + X=
120
30%
500.000
X= = R$ 4.166,67 (valor
120
arredondado)
Exs.:
a) Qual o preço que é possível vender um produto que
teve seu custo de R$ 700,00, para se ter um lucro final
de 15%? Resposta: O lucro da operação foi de R$ 4.166,67
Solução:
C*L=V » 100% + 15% = 115% d) Uma geladeira foi vendida com um lucro final de 35%.
Calcule o valor da venda, sabendo que o lucro na operação
foi de R$ 250,00.
R$ 700,00 ................ 100% (custo da operação)
....................X ........................ 115% (venda da operação)
115 x 700
X= Solução:
100
80500 C + L = V -à 100% + 35% = 135%
X= = R$ 805,00
100
250 ................ 35% (lucro da operação)
O valor do produto será de R$ 805,00 X .................... 135% (venda da operação)
135 x 250
b) Qual o preço que é possível vender um produto que teve X=
seu custo de R$ 300,00, para se ter um lucro final de 50%? 35
33750
Solução: X= = R$ 964,29 (valor
35
arredondado)
Resumo teórico 24

25. Pré-vestibulinho
Matemática
Resposta: O valor da venda foi de R$ 964,29 1.200 ........... 100% (custo da operação)
.......................X ............ 40% (prejuízo da operação)
1200 x 40
X=
e) Uma casa foi comprada por R$ 20.000,00, e revendida 100
em sucessivos negócios com lucros seqüentes de 15%, 25%
e 30%. Nesta operação, qual foi o último preço de venda da 48000
X= = R$ 480,00
casa? 100
Solução: Resposta: O prejuízo desta operação foi de R$
480,00.
1ª operação de venda (15% de lucro) ###
C + L = V » 100% + 15% = 115% Exercícios
20.000 .............. 100% (custo da operação) 1.(SENAI) Um vendedor ambulante vende, diariamente, 50
X ................. 110% (venda da operação) unidades de churrasco grego acompanhado de um copo de
suco. O churrasco mais o copo de suco são vendidos por R$
X = 20.000 . 110 / 100 = R$ 22.000,00 1,50. O custo do referido produto (churrasco mais suco) é de
R$ 0,90. Se o vendedor trabalhar dez dias consecutivos nessas
condições, o lucro obtido corresponderá a
....
a. R$ 1.200,00.
b. R$ 900,00.
2ª operação de venda (25% de lucro) c. R$ 750,00.
C + L = V » 100% + 25% = 125% d. R$ 550,00.
e. R$ 300,00.
(valor da casa R$ 22.000,00)
22.000 ............... 100% (custo da operação) 2. (SENAI 2008) Um comerciante descontou em um banco um
X ................... 125% (venda da operação) cheque pré-datado para trinta dias no valor de
R$ 12.000,00. Se o banco utiliza uma taxa de desconto de 5,2%
ao mês, o valor líquido recebido
X = 22.000 . 125 / 100 = R$ 27.500,00
pelo comerciante foi de
a. R$ 11.994,80.
.... b. R$ 11.376,00.
c. R$ 9.692,30.
3ª operação de venda (30% de lucro) d. R$ 6.952,80.
C + L = V » 100% + 30% = 130% e. R$ 5.760,00.
(valor da casa R$ 27.500,00)
3. (SENAI 2008) Para participar de uma novela, uma atriz
que pesava 100 kg em 1º de março de 2006, submeteu-se a
um regime alimentar. O resultado obtido foi tal que o seu
peso, a cada mês, sofreu uma perda de 10% em relação ao
27.500 ............ 100% (custo da operação)
seu peso do mês anterior. Nessas condições, em 1º de
......................X ................ 130% (venda da operação)
junho de 2006, a atriz passou a “pesar”.
Nota: o termo “peso” corresponde a massa.
27500 x 130 a. 58,6 kg.
X= = R$ 35.750,00
100 b. 60,0 kg.
c. 65,4 kg.
Resposta: O valor final da casa foi de R$ 35.750,00 d. 70,0 kg.
e. 72,9 kg.
4.(Trajano 2008) Na sua edição de 27 de julho de 2008, o
f) Uma pessoa vendeu um aparelho de som que custou
jornal Folha de S. Paulo divulgou uma pesquisa sobre o
R$ 1.200,00 com 40% de prejuízo sobre o custo. Qual foi o
perfil do jovem brasileiro, a qual apresenta indicadores que
prejuízo desta operação?
contribuem com os estudos sobre a exclusão social no
Brasil.
Solução:
Resumo teórico 25

26. Pré-vestibulinho
Matemática
Para a pergunta “Você estuda?”, os dados obtidos foram: (formada por cerca de trinta bairros, em geral periféricos e
com pior poder aquisitivo).
De acordo com as idéias do texto e as informações
Para os jovens que estudam foi feita a pergunta “Em que auxiliares, é correto afirmar que
ano você está?”, e os dados obtidos foram:
(A) a distribuição territorial desses equipamentos de lazer
atende com justiça e igualdade às necessidades de
Nível de Ensino Porcentagem
todos os moradores do município.
Ensino Médio 52% (B) os moradores das Zonas 1 e 2 são cidadãos privilegiados
entre os moradores restantes do município, pois
Ensino Superior 20% estes últimos fi cam mal servidos territorialmente de
diversas oportunidades de lazer.
Ensino Fundamental 16%
(C) os moradores da Zona 3 podem ser considerados mais
Cursinho 4% cidadãos por terem mais facilidade de acesso às
múltiplas oportunidades de lazer do município.
Pós-graduação 2% (D) os moradores da Zona 2 são menos cidadãos e sofrem
duas vezes com a pobreza, pois são contemplados
Supletivo 2% territorialmente com menos oportunidades de lazer que os
Outras 4% outros moradores do município.
(E) a distribuição territorial desigual dos equipamentos de
lazer não agrava a pobreza e não interfere nos direitos
De acordo com os dados fornecidos e admitindo que há de exercício de cidadania dos moradores do município.
cerca de 35 milhões de jovens brasileiros, então o número
de jovens brasileiros que estão no Ensino Superior é
(A) 3 430 000.
(B) 3 570 000.
(C) 4 000 000. 6.(PSS-SEE/SP) Em um determinado condomínio, paga-se
(D) 7 000 000. atualmente um salário mensal de R$ 1418,00 para um
zelador. Com todos os encargos, esse funcionário custa ao
(E) 8 918 000.
condomínio R$ 2392,00. Após uma análise de mercado e
algumas reflexões junto à associação de trabalhadores que
5.(Trajano 2007) Analise o texto e a tabela a seguir. representa essa classe, a empresa administradora concluiu
A possibilidade de ser mais ou menos cidadão depende, que deveria atualizar esse salário em 4,5% referentes ao
em larga medida, do ponto do território onde se vive. ano de 2007, e mais 4% referentes ao ano de 2008.
Muitos moradores da periferia tornam-se cidadãos A taxa de reajuste do salário do zelador, após essas
incompletos por terem menos acesso aos serviços urbanos atualizações, será:
e direito à cidade como um todo. Morar na periferia é se a) 8,5%.
condenar duas vezes à b) Maior que 8,5%.
pobreza: além das desigualdades socioeconômicas, o pobre c) 16,5%.
sofre com a má distribuição territorial dos serviços públicos d) 18%.
como saúde, educação, segurança e lazer. e) Maior que 18%.
(Adaptado de: SANTOS, Milton. O espaço do cidadão. São Paulo, Nobel,
1987, pp. 81 e 115.)
O município do Rio de Janeiro pode ser dividido em
três grandes zonas. Nas Zonas 1 e 2 (formadas
respectivamente pelo centro histórico e seis bairros nobres
com melhor poder aquisitivo) o território e a quantidade de
moradores são muito menores do que os da Zona 3
Resumo teórico 26

27. Pré-vestibulinho
Matemática
2º Passo:
9. EQUAÇÕES DO 1º E 2º GRAUS » Substituir esses coeficientes no discriminante:  = b - 4ac
2
....PROBLEMAS DE APLICAÇÃO
 = b2 - 4 a c
9.1. Equação do 1º grau  = ( -7 )2 - 4 ( 1 ) · (12 )
 = 49 – 48
É toda equação do tipo ax + b = 0, com a  *, e b  =1
.
Para determinar a solução de uma equação do 1º grau, 3º Passo :
procedemos assim: » Observar o valor de “” e verificar se tem raiz(es) reais
𝐛 Podemos observar que  = 1 ,
x = -
ax + b = 0  ax = - b  𝐚
então  >0, a equação terá duas raízes diferentes
b
Logo, S = - 4º Passo :
a » Calcular essa(s) raízes...
9.1.1. Problemas de aplicação
−𝑏± 
x1 e x2 =
2𝑎
− −7 ± 1
x1 e x2 =
2( 1)
9.2. Equação do 2º grau 7 ±1
x1 e x2 =
2
Toda equação na variável x do tipo ax2 + b + c = 0,
com a  *, b  e c
x1 =
7+1
2
 x1 =
8
2
 x1 = 4
Discriminante:  = b - 4ac
2 7−1
x2 =  x2 =
6
2
 x2 = 3
2
Se  > 0 ou  = 0 , Então x1 e x2 são as raízes da
equação.
5º Passo :
Para calcularmos as raízes fazemos: » Representar a resposta:
−𝑏±  S = { -3, 4 }
x1 e x2 = , sabendo que
2𝑎
(2º Tipo) =0
Exs. » Resolva a equação: x2 – 8x + 16= 0
(1º Tipo) >0
1º Passo :
2
» Resolva a equação:
2
x – 7x + 12= 0 » Determinar os coeficientes a, b, e c em x – 8x + 16 =
0
1º Passo :
2
» Determinar os coeficientes a, b, e c em x – 7x + 12= a=1
b = -8
0
Obs. Quando não “aparecer c = 16
2
a=1 um número na frente do “ x ”,
ou do “x” devemos lembrar 2º Passo:
b = -7
» Substituir esses coeficientes no discriminante:  = b - 4ac
2
c = 12 que lá está o 1.
Resumo teórico 27

28. Pré-vestibulinho
Matemática
 = b2 - 4 a c 3º Passo :
 = ( -8 )2 - 4 ( 1 ) · (16 ) » Observar o valor de “” e verificar se tem raiz(es) reais
 = 64 – 64 Podemos observar que  = -8 ,
=0
então  < 0, a equação não admite raízes reais
3º Passo : “ negativo”
» Observar o valor de “” e verificar se tem raiz(es) reais
Podemos observar que  = 0 ,
4º Passo :
» Representar a resposta:
então  = 0, a equação terá duas raízes iguais
Obs.: Podemos também
S={ } representar o conjunto
4º Passo : vazio desta forma: S = 
» Calcular essa(s) raízes caso existam...
−𝑏± 
Resumindo
x1 e x2 =
2𝑎
 > 0  duas raízes reais diferentes
− −8 ± 0
x1 e x2 =  = 0  raízes reais e iguais
2( 1)
8 ±0  < 0  não possui raízes reais
x1 e x2 =
2
8+0
x1 =  x1 =
8
2
 x1 = 4 9.2.1. Problemas de aplicação
2
8−0 1.(SENAI 2008) Na temporada do verão passado, um
x2 =  x2 =
8
2
 x2 = 4 comerciante vendeu picolés, cuja renda (p) em reais, no
2 2
final de cada dia, varia de acordo com a expressão p = x -
11x - 10, em que x indica a quantidade de picolés vendidos
Obs.: Podemos representar
5º Passo : no dia. Se num determinado dia, a renda final foi de R$
um único número, pois as
» Representar a resposta: 200,00, pode-se afirmar que o comerciante vendeu naquele
respostas são iguais
dia
S={4} a. 12 picolés. d. 21 picolés.
b. 15 picolés. e. 27 picolés.
c. 19 picolés.
(3º Tipo) <0 ( negativo)
» Resolva a equação: 3x2 – 4x + 2= 0
2.(Trajano 2008) Considere um número inteiro positivo tal
que quatro quintos da soma desse número com 36 é igual à
1º Passo :
2 diferença entre o dobro desse número e 6. A soma dos
» Determinar os coeficientes a, b, e c em 3x – 4x + 2=
algarismos do número considerado é
0
(A) 11. (B) 12. (C) 13. (D) 14. (E) 15.
a=3
b = -4
c=2
3.(PSS-SEE/SP) Deseja-se construir uma calçada
2º Passo: contornando-se dois lados consecutivos de um jardim cuja
» Substituir esses coeficientes no discriminante:  = b - 4ac
2
forma é
retangular, conforme mostra a figura abaixo:
 = b2 - 4 a c
 = ( -4 )2 - 4 ( 3 ) · (2 )
 = 16 – 24
 = -8
Resumo teórico 28

29. Pré-vestibulinho
Matemática
Deseja-se que a calçada ocupe uma área de 15m². A
equação que permite calcular o valor de x é:
a) x² − 9x + 15 = 0.
b) x² − 15x + 10 = 0.
c) x² − 15x + 20 = 0.
d) x² − 20x − 15 = 0.
e) x² − 9x − 20 = 0.
Resumo teórico 29

30. Pré-vestibulinho
Matemática
10. SISTEMAS DE EQUAÇÕES
....DO 1º GRAU
1º passo: vamos isolar o y na primeira equação para
10.1. Métodos de resolução de sistemas de podermos substituir na Segunda equação.
equações do 1º grau
Além de saber armar o sistema é bom saber fazer a
escolha pelo método mais rápido de resolução.
Vou apresentar três métodos sendo que o mais utilizado é
o método da adição. 2º passo: Substituir y = 6 – 2x, na segunda equação para
encontrar o valor de x.
10.1.1. Método da adição
Este método consiste em deixar os coeficientes de uma
incógnita opostos. Desta forma, somando-se membro a
membro as duas equações recai-se em um equação com
uma única incógnita.
Ex:
3º passo: Substituir x = 4 em y = 6 – 2x, para encontrar o
valor de y.
1º passo: vamos multiplicar a primeira linha por -1 para
podermos cortar –2x com 2x
y = 6 – 2x
y = 6 – 2.4
y=6–8
y = -2
4º passo: dar a solução do sistema.
S = { (4, -2) }
2º passo: Substituir y = - 2, em qualquer um das equações
acima e encontrar o valor de x.
10.1.3. Método da comparação
Esse método consiste em compararmos as duas equações
do sistema, após termos isolado a mesma variável ( x ou y)
nas duas equações:
Ex.:
3º passo: dar a solução do sistema. Resolver o sistema pelo método da comparação
S = { (4, -2) } x + 2y = 2
10.1.2. Método da substituição
x+y=3
Este método consiste em isolar uma incógnita numa
equação e substituí-la na outra equação do sistema dado,
recaindo-se numa equação do 1º grau com uma única 1º passo: vamos isolar as mesmas variáveis nas duas
incógnita. equações
Ex:
Resumo teórico 30

31. Pré-vestibulinho
Matemática
x + 2y = 2 »isolando “x” temos x = 2 - 2y
x+y=3 »isolando “x” temos x = 3 - y
2º passo: vamos igualar essas variáveis e calcular o valor de
x
Exercícios
1.(Trajano 2008) Imagine que antes de posar para a foto de
família, o pai, não resistindo à tentação diante de um
maravilhoso bolo recheado e de uma divina torta de limão,
comeu uma e meia fatia de bolo recheado e duas fatias de
torta de limão, consumindo 1 482 quilocalorias. Por sua vez,
a mãe comeu meia fatia do mesmo bolo e três quartos de
uma fatia da mesma torta, consumindo 606 quilocalorias.
Preocupada com o abuso das iguarias consumidas, a mãe se
perguntou: “Quantas quilocalorias tem uma fatia de bolo
recheado? E quantas tem uma fatia de torta de limão?”
Para resolver o problema, a mãe montou um sistema de
duas equações, representando por b a quantidade de
quilocalorias de uma fatia do bolo recheado e por t a
quantidade de quilocalorias de uma fatia da torta de limão,
levando em consideração que o bolo foi fatiado
uniformemente e a torta também.
Assim sendo, o sistema que ela montou é equivalente ao
sistema
(A) 3b + 4t = 1 482
b + 2t = 1 212
(B) 3b + 4t = 2 964
2b + 3t = 2 424
(C) 3b + 4t = 1 212
b + 3t = 2 964
(D) 3b + 2t = 2 964
b + 2t = 1 212
3b + 2t = 1482
(E) b + 3t = 606
Resumo teórico 31

32. Pré-vestibulinho
Matemática
11. PLANO CARTESIANO 1. (COTIL 2002) Observando o plano cartesiano a seguir,
dê os pares ordenados de cada ponto representado no
gráfico.
11.1. INTRODUÇÃO
Traçando dois eixos – Ox, ao qual chamaremos de eixos das
abscissas, e Oy, que chamaremos eixos das ordenadas – de
forma que ambos se interceptem perpendicularmente em
O, o plano sobre o qual construímos esses eixos fica dividido
em quatro quadrantes. Observe:
COTIL ( , )
Restaurante ( , )
Todos os pontos do plano poderão ser identificados
por dois valores ordenados que chamamos par ordenado e Cantina ( , )
representamos por ( x, y ). Assim, para todo ponto no
plano cartesiano temos um par ordenado, e para todo par Gráfica ( , )
ordenado temos um ponto correspondente no plano.
Essa correspondência chamaremos de sistema cartesiano 2.(SENAI) Um mapa rodoviário foi desenhado sobre o sistema
ortogonal e o plano será chamado de plano cartesiano ( o de coordenadas cartesianas, para localizar uma reserva
termo ortogonal refere-se ao perpendicularismo entre os florestal. O segmento AB indica um trecho da rodovia principal,
eixos). Vamos ver os pontos do plano correspondentes aos o segmento AC a estrada de acesso à reserva e M é o ponto
pares ordenados A(3,1), B(-2,3), C(-4,-3), D(0,-2) e E(-5,0) médio de AB. No mapa, a estrada AC mede, em quilômetros,
a. 4. c. 6. e. 8.
b. 5. d. 7.
EXERCÍCIOS
Resumo teórico 32

33. Pré-vestibulinho
Matemática
12. FUNÇÃO DO 1º GRAU
12.1.Definição
x y
0 -1
Chama-se função polinomial do 1º grau, ou função
afim, a qualquer função f de IR em IR dada por uma lei da 0
forma
f(x) = ax + b, onde a e b são números reais dados e a 0.
Na função f(x) = ax + b, o número a é chamado de
coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
Já vimos que o gráfico da função afim y = ax + b é uma
f(x) = 5x - 3, onde a = 5 e b = - 3 reta.
f(x) = -2x - 7, onde a = -2 e b = - 7 O coeficiente de x, a, é chamado coeficiente angular da
f(x) = 11x, onde a = 11 e b = 0 reta e, como veremos adiante, a está ligado à inclinação da
reta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da
reta. Para x = 0, temos y = a · 0 + b = b. Assim, o coeficiente
linear é a ordenada do ponto em que a reta corta o eixo Oy.
12.2.Gráfico
EXERCÍCIOS
O gráfico de uma função polinomial do 1º grau, y = ax +
b, com a 0, é uma reta oblíqua aos eixos Ox e Oy.
1.(SENAI 2008) A função horária de um ponto material é
Exemplo: dada por S = 15 - 3 t, com t em segundos e S em metros.
Podemos afirmar que o ponto material passa pela origem
Vamos construir o gráfico da função y = 3x - 1: dos espaços no instante igual a
Como o gráfico é uma reta, basta obter dois de seus a. 3 s.
pontos e ligá-los com o auxílio de uma régua: b. 4 s.
c. 5 s.
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um d. 6 s.
ponto é (0, -1). e. 10 s.
1
b) Para y = 0, temos 0 = 3x - 1; portanto, x = e 2.(SENAI 2008) Duas forças horizontais, de sentidos
3
opostos, com intensidades 10 e 15 N, atuam num corpo que
outro ponto é ( 1 ,0)
3
está livre de atrito e que tem massa de 2,5 kg. A aceleração
2
que a força resultante imprime ao corpo é, em m/s , de
a. 1,5.
Marcamos os pontos (0, -1) e ( 1 ,0)
3
no plano b. 2,0.
c. 4,0.
cartesiano e ligamos os dois com uma reta.
d. 5,0.
e. 7,5.
3.(SENAI 2008) A energia mecânica de um sistema
conservativo é de 180 J. Se num dado instante a energia
cinética é de 120 J, a energia potencial é, nesse mesmo
instante, de
a. 180 J.
b. 120 J.
c. 100 J.
Resumo teórico 33

34. Pré-vestibulinho
Matemática
d. 80 J.
e. 60 J.
4.(TRAJANO 2008) Imaginando-se que o barco de Hagar
desloque-se por um mar, onde a densidade da água é
constante em qualquer ponto, pode-se afirmar que a força
de empuxo que age no navio
(A) diminui com o aumento da carga transportada.
(B) diminui com a diminuição da carga transportada.
(C) aumenta com a diminuição de carga transportada.
(D) aumenta o espaço percorrido devido ao aumento de
velocidade média.
(E) diminui a velocidade média, provocando uma
diminuição no espaço percorrido.
Resumo teórico 34

35. Pré-vestibulinho
Matemática
13. FUNÇÃO EXPONENCIAL
13.1.Definição
Função exponencial é uma função na qual a
variável (incógnita) se encontra no expoente.
A função exponencial pode ser escrita de forma geral,
veja como:
x
f : R → R*+ tal que f(x) = a , sendo que a R*+ e a ≠ 1.
Essa representação significa: dada uma função dos • Esse gráfico representa uma função exponencial
reais para os reais positivos, menos o zero, sendo que a crescente onde a > 1.
função exponencial terá base “a” onde “a” só poderá
assumir valores positivos diferentes de zero e diferentes
de 1. • Imagem e domínio: x1 e x2 são os valores do domínio
dessa função e os valores de y1 e y2 são os valores da
imagem dessa função, sendo que a imagem será sempre
(quando o valor da base é maior que 1) um valor real
Veja alguns exemplos de funções exponenciais: positivo diferente de zero.
x
f(x) = 3 , função exponencial de base 3 e expoente x
(variável).
y
f(y) = 3 , função exponencial de base 3 e expoente y
(variável).
5
x
f(x) = 0,5 , função exponencial de base 0,5 e expoente x
(variável).
f(x) = , função exponencial de base 5 e expoente x
(variável).
• Esse gráfico representa uma função exponencial
13.1. Gráfico de função exponencial decrescente onde
0 < a < 1.
A construção de gráficos de função exponencial segue
dois modelos, quando o valor da base é maior que 1 e • Imagem e domínio: x1 e x2 são os valores do domínio
quando o valor da base está entre 0 e 1. Veja esses modelos dessa função e os valores de y1 e y2 são os valores da
esboçados: imagem dessa função, sendo que a imagem será sempre
(quando o valor da base é maior que 1) um valor real
x
Dada a função f(x) = a , veja como ficarão os positivo diferente de zero.
gráficos dependendo do valor de a (base).
Os dois tipos de gráficos possuem características
semelhan-tes, essas são características para qualquer
gráfico de função exponencial.
• O gráfico (curva) nunca irá interceptar o eixo x, pois a
função exponencial não possui raiz.
Resumo teórico 35

36. Pré-vestibulinho
Matemática
• O gráfico (curva) irá cortar apenas o eixo y e sempre será
no ponto 1, sendo que os valores de y sempre serão
positivos.
EXERCÍCIOS
1.(SENAI 2008) O volume d’água que resta, após abrir o
registro de uma caixa completamente cheia d’água, pode
2 t-2
ser obtido por meio da expressão: V = 900 ( ) , em que
3
V indica o volume em litros d’água que resta na caixa após o
registro ficar aberto t minutos. O tempo para que restem na
caixa 600 L é
a. 2,0 minutos.
b. 2,6 minutos.
c. 2,8 minutos.
d. 3,0 minutos.
e. 3,5 minutos.
Resumo teórico 36

37. Pré-vestibulinho
Matemática
você guarde os dois seguintes:
14. ELEMENTOS FUNDAMENTAIS
DA ...GEOMETRIA PLANA E  Toda reta é formada por infinitos pontos.
 Todo plano contém infinitas retas e também infinitos
SEMELHANÇA ...DE FIGURAS pontos
PLANAS.
14.1.2. Elementos básicos
14.1. Introdução a geometria a) Semi-reta: Dada uma reta qualquer, um ponto dessa
reta divide a mesma em duas semi-retas.
14.1.1. Conceitos primitivos
Ex.
São conceitos que não tem definição, aceitamos como
verdadeiro para a partir disso formar uma teoria. Indica-se AB
a) Ponto: Ponto não tem definição, apenas uma idéia
intuitiva. O ponto é adimensional, isto é, não tem b) Segmento de reta: Dada uma reta qualquer e dois pontos
dimensão, e podemos representá-lo por uma letra dessa reta, o segmento e a região limitada entre esses dois
maiúscula do nosso alfabeto. po
Ex.
Exs.: A ( Ponto “A”)
G Indica-se AB
c) Semiplano: Sabemos que um plano contém infinitas
b) Reta: Podemos ter uma idéia de uma reta como infinitos retas. Com uma reta r, dividimos o plano em dois
pontos alinhados. A reta é unidimensional, uma conjuntos de pontos, situados cada um em um dos “lados
dimensão, e podemos representá-la por uma letra
da reta”
minúscula do nosso alfabeto, ou por dois de seus Chama-se semiplano (de origem r) cada um dos
pontos. conjuntos de pontos em que um plano fica dividido por
uma reta r, incluindo a própria reta.
Exs.:
Ex.
ou
c) Plano: Podemos ter uma idéia de plano como sendo uma
superfície plana de tamanho infinito. O plano é
bidimensional, duas dimensões, e podemos representá-
lo por uma letra minúscula do alfabeto grego.
Ex.
α
Plano Alfa
Ponto, reta e plano relacionam-se entre si de certas
proprie-dades não demonstráveis, chamadas postulados.
Entre os postulados da geometria plana, é importante que
Resumo teórico 37

38. Pré-vestibulinho
Matemática
14.2. Ângulos
e) Ângulos complementares: Dois ângulos são complemen-
tares quando a soma de suas medidas é igual a 90º
14.2.1. Definição
Exs.:
70º + 20º = 90º α + β = 90º
Ângulo é a região formada por duas semi-retas a partir
70º é o complementar de α é o complementar
da mesma origem. Cada semi-reta é chamada de lado do
........... 20º e vice-versa de β e vice-versa
ângulo e o ponto de origem é denominado vértice.
â = ângulo
OA = semi-reta
OB = semi-reta f) Ângulos suplementares: Dois ângulos são suplementares
quando a soma de suas medidas é igual a 180º
Podemos também representar o ângulo como:
AÔB, BÔA ou Ô. Ex.:
14.2.2. Classificação dos ângulos
a) Ângulo agudo: ângulo menor que 90º
Exs.: g) Ângulos replementares: Dois ângulos são replementares
quando a soma de suas medidas é igual a 360º
Ex.:
b) Ângulo obtuso: ângulo que possui uma medida maior
que 90º e menor que 180º
h) Ângulos opostos pelo vértice: Dois ângulos são opostos
pelo vértice quando os lados de um são semi-retas opostas
Exs.:
dos lados do outro
Ex.
c) Ângulo reto: ângulo que possui uma medida igual a 90º
Exs.:
α e θ = são opostos pelo vértice
β e σ = são opostos pelo vértice
Atenção:
Obs.: Quando duas retas formam entre si um ângulo de 90º,
denominamos retas perpendiculares.  Todos os ângulos opostos pelo vértice (o.p.v.) são
congruentes, isto é, possuem a mesma medida:
d) Ângulo raso ou de meia volta: ângulo que possui uma α=θ e β=σ
medida igual a 180º
Ex.:
Resumo teórico 38

39. Pré-vestibulinho
Matemática
 Duas retas concorrentes que formam quatro Ângulos Obs.: Duas retas coincidentes também são paralelas; neste
retos são chamadas de retas perpendiculares. caso eles tem todos os pontos em comum.
14.3.2. Paralelas com transversais
Dadas duas retas paralelas, chama-se reta transversal
14.2.3. Bissetriz de um ângulo
qualquer reta que intercepte ambas as paralelas. Essa
transversal determina, na intersecção com uma das
É a semi-reta de origem no vértice do ângulo e que o paralelas, quatro ângulos e, na intersecção com outra
divide em dois outros ângulos de mesma medida. paralela, mais quatro ângulos.
14.2.4 Medidas de ângulos
A principal unidade usada para se medir ângulos (tanto
na geometria quanto na vida prática) é o grau.
A unidade grau é subdividida em unidades menores (
submútiplos) que são o minuto e o segundo, de tal modo
que:
Na figura certos pares de ângulos recebem nomes especiais
 Cada grau é formado por 60 minutos: 1º = 60’
 Cada minuto é formado por 60 segundos 1’ = 60”  Ângulos correspondentes: â e m, ^ e n, c e p, d eq
^ b ^ ^ ^ ^ ^
^ ^ ^ ^
 Ângulos alternos internos: c e m, d e n
^ ^ ^ ^
 Alternos externos : a e p, b e q
^ ^ ^ ^
Ângulos colaterais internos: d e m, c e n
14.3. Paralelismo de Retas ^ ^ ^ ^
 Ângulos colaterais externos: a e q, b e p
Duas retas são paralelas quando, estando contidas no
mesmo plano, não possuem nenhum ponto em comum.
Teorema fundamental do paralelismo de retas
Duas restas paralelas, cortadas por uma transversal,
determinam ângulos correspondentes congruentes,
isto é de mesma medida.
14.3.1. Postulado de Euclides
Por um ponto fora de uma reta, existe uma única reta
paralela à reta dada.
Resumo teórico 39

40. Pré-vestibulinho
Matemática
Chamaremos de polígonos as regiões do plano cujos
Na figura acima temos: ^ = n , c = ^ , ^ = ^ então:
b ^ ^ p d q, contornos são formados apenas por segmentos
Duas retas paralelas, cortadas por uma transversal,
determinam ângulos alternos congruentes Dessa forma, as figuras B, C e D são polígonos, enquanto
que A e E não.
Em todos os polígonos temos os seguintes elementos:
...........................Lados, vértice e diagonais.
Observe a figura que segue:
Duas retas paralelas cortadas por uma transversal,
determinam ângulos colaterais suplementares, isto
é, suas medidas somam 180º
Lados: __ __ __
São segmentos que cortam os contornos: AB, BC, CD, etc.
Vértices:
São pontos comuns a dois lados consecutivos: A, B, C, D,
etc.
Diagonais:
__ __ __ __
São os segmentos que unem dois vértices não consecutivos:
AE, AD, BF, CE, etc.
14.4. Polígonos
Observe as figuras abaixo:
Nas figuras B, C e D, o contorno é formado exclusiva-
mente por segmentos; nas figuras A e E, o contorno tem
partes curvas.
Resumo teórico 40

41. Pré-vestibulinho
Matemática
14.4.1 Classificação 14.5. Semelhança de figuras planas
A classificação dos polígonos pode ser feita de dois modos
diferentes: ou em relação ao número de lados, ou em 14.5.1. Semelhança de Triângulos
relação ao número de ângulos.
Teorema (AAA)
Assim temos:
Dois triângulos são semelhantes quando possuem
Ao nº de lados Ao nº de lados respectivamente congruentes as medidas dos ângulos, e
3 Trilátero Triângulo as medidas dos lados correspondentes, respectivamente
4 Quadrilátero Quadrilátero proporcionais.
5 Pentalátero Pentágono
6 Hexalátero Hexágono
7 Heptalátero Heptágono
8 Octalátero Octógono Lados correspondentes ou homólogos: lados que se opõem
9 Enealátero Eneágono a ângulos congruentes
10 Decalátero Decágono
11 Undecalátero Undecágono
12 Dodecalátero Dodecágono
...
...
...
15 Pentadecalátero Pentadecágono
...
...
...
20 Icosalátero Icoságono
Os polígonos ainda podem ser :
^ ^ ^
A ^
A´
REGULARES: quando possuem:
- todos os ^ ^
ângulos internos congruentes ^
B ^
B´
- todos os lados também congruentes
^ ^ ^
C ^
C´ ABC ~A´B´C´
IRREGULARES:
- quando pelo menos uma das duas condições acima não é AB BC CA
verificada = =
A´B´ B´C´ C´A´
Nota: ~ ....lê-se: semelhante
14.4.2. Diagonal
Denomina-se diagonal de um polígono o segmento de reta
Teorema (LAL)
que une dois vértices não-consecutivos dele.
Dois triângulos são semelhantes quando possuem
𝐧 𝐧−𝟑
Número de diagonais: d = congruente a medida de um ângulo compreendido entre
𝟐 lados proporcionais.
Resumo teórico 41

42. Pré-vestibulinho
Matemática
^
A ^
A´ sua decomposição em triângulos respectivamente
ABC ~ A´B´C´ semelhantes.
AB AC Teorema
=
A´B´ A´C´ As medidas dos perímetros de dois polígonos
semelhantes estão entre si assim como a razão de dos lados
correspondentes.
Teorema (ALA) Obs.:
Perímetro  é a soma das medidas dos lados de um
Dois triângulos são semelhantes quando possuem as polígono.
mesmas medidas de dois ângulos congruentes.
^
A ^
A´
ABC ~A´B´C´
^ ^
C C´
Teorema (LLL)
Dois triângulos são semelhantes quando possuem as
medidas dos três lados respectivamente proporcionais.
AB BC CA
= B´C´ = C´A´  ABC ~A´B´C´
A´B´
14.5.2. Semelhança de Polígonos
Definição
Dois polígonos são semelhantes quando possuem o
mesmo número de lados, as medidas dos ângulos
respectivamente congruentes e as medidas dos lados
respectivamente proporcionais.
Teorema
Dois polígonos são semelhantes quando for possível a
Resumo teórico 42

43. Pré-vestibulinho
Matemática
b)
15. RELAÇÕES MÉTRICAS NO
.....TRIÂNGULO RETÂNGULO
15.1. Introdução
Triângulo retângulo é aquele que tem um ângulo reto
(90º graus).
Solução:
2 2 2
a =b +c
2 2 2
6 =x +x
2
2x = 36
2
x = 18
x = 18
x=3 𝟐
15.2. Teorema de Pitágoras
15.3. Elementos de um triângulo retângulo
Num triângulo retângulo, o quadrado da hipotenusa é Seja o triângulo retângulo:
igual a soma dos quadrados dos catetos.
a2 = b2 + c2
Exs.:
Aplicando o teorema de Pitágoras, calcule o valor de x;
a)
a = medida da hipotenusa BC
b = medida do cateto AC
c = medida do cateto AB
h = medida da altura AE
Solução:
m = medida da projeção AC sobre a hipotenusa
2 2 2
a =b +c n = medida da projeção AB sobre a hipotenusa
2 2 2
x =3 +4
2
x = 9 + 16
2 No triângulo ABC, são válidas as relações métricas:
x = 25
x = 25
x=5
Resumo teórico 43

44. Pré-vestibulinho
Matemática
b)
Solução: y · 3 = 2· 3
3y = 6
6 3
y=
3
· 3
b2 = m · a c2 = n · a
6 3
y=
3
y =2 𝟑
c)
a·h=b·c
y = 4 ·9
2
Solução:
2
y = 36
y= 36
y=6
15.3.1. Cálculo da altura de um triângulo eqüilátero
2
h =m·n Considerando o triângulo ABC abaixo, temos:
Exs:
Calcule o valor de x, nos seguintes triângulos retângulos:
L 2 = (L /2)2 + h2
a) e a altura será dada
pela .......fórmula:
L 3
h=
y = 2· 8 2
2
Solução:
2
y = 16
y = 16
y =4
Resumo teórico 44

45. Pré-vestibulinho
Matemática
15.3.2. Cálculo da diagonal de um quadrado
Considerando o quadrado ABCD e uma diagonal BC.
No triângulo BCD, temos:
2 2 2
d =L +L
2 2
d =2L
d=L 2
Resumo teórico 45

46. Pré-vestibulinho
Matemática
16. RAZÕES TRIGONOMÉTRICAS 2) Calcular Sen, Cos e Tg de α
Definimos no triângulo retângulo:
9 3

cateto oposto
Sen α = = Sen α =
hipotenusa 15 5
cateto oposto
Seno (Sen)=
hipotenusa 12 4

cateto adjacente
Cos α = = Cos α =
hipotenusa 15 5
cateto adjacente
Cosseno(Cos) =
hipotenusa
9 3

cateto oposto
Tg α = = Cos α =
cateto adjacente 12 4
cateto oposto
Tangente(Tg) =
cateto adjacente
Exs.:
16.1. Ângulos Notáveis
1) Calcular o seno, cosseno e a tangente do ângulo α
As razões trigonométricas dos ângulos de 30º, 45º e
60º aparecem freqüentemente nos problemas, tornando-
se conveniente a memorização desses valores.
30º 45º 60º
α
1 2 3
Sen
2 2 2
3 2 1
cateto oposto c Cos
Sen α = = 2 2 2
hipotenusa a
3
Tg 1 3
cateto adjacente b 3
Cos α = =
hipotenusa a
cateto oposto c
Tg α = =
cateto adjacente b
Resumo teórico 46

47. Pré-vestibulinho
Matemática
Exs.:
1) Calcule o valor de x no triângulos retângulo que segue:
Solução:
x
....................Cos 60º =
10
1 x
=
2 10
2x = 10
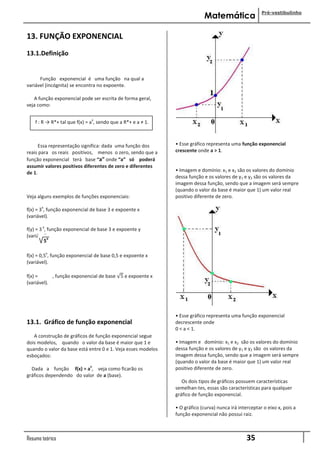
x =5 Propriedades:
- Domínio: R
2) No triângulo ABC da figura seguinte, determine as - Imagem: [-1;1]
- Período: 2πrad
medidas a e c indicadas.
Solução
10
Sen 30º =
𝑎
Função Co-seno
1 10
=
2 a
Dado um ângulo cuja medida é dada em radianos é x,
a = 2 · 10 chamamos de função co-seno à função que associa a cada x
∈ R o número (cosx) ∈ R. Indicamos essa função por:
a = 20
f(x) = cos(x)
O gráfico da funcão co-seno, no cartesiano, será uma curva
Aplicando o Teorema de Pitágoras denominada co- senóide. Atribuindo valores ao arco x,
2
a = b + c
2 2 pode-se chegar ao gráfico.
2 2 2
.....................................................................20 = 10 + c
2
c = 300
c = 300
c = 10 𝟑
Funções trigonométricas
Função Seno Propriedades:
- Domínio: R
Dado um ângulo cuja medida é dada em radianos é x, - Imagem: [-1;1]
chama-mos de função seno à função que associa a cada x ∈ - Período: 2πrad
R o nu-mero (senx) ∈ R. Indicamos essa função por:
Função Tangente
f(x) = sen(x)
Dado um ângulo cuja medida é dada em radianos é x,
O gráfico da função seno, no plano cartesiano, será uma
chamamos de função tangente à função que associa a cada
curva denominada senóide. Atribuindo valores ao arco x,
x ∈ R/x ≠ π/2+kπ o número (tgx) ∈ R. Indicamos essa função
pode-se chegar ao gráfico.
por:
f(x) = tg(x)
Resumo teórico 47

48. Pré-vestibulinho
Matemática
O gráfico da função tangente, no cartesiano, será uma curva 3.(Trajano 2008) O quadrilátero ABCD pode ser
denominada tangentóite. Atribuindo valores ao arco x, decomposto nos triângulos ABD e BCD, conforme a figura.
pode-se chegar ao gráfico.
(A) 0,4.
(B) 0,5.
(C) 0,6.
(D) 0,7.
(E) 0,8.
Propriedades:
- Domínio:
- Imagem: R
- Período: πrad
Exercícios
1.(SENAI 2008) Numa determinada região, onde lobos são
predadores e ovelhas são as presas, a população de ovelhas
P (em milhares) variou de acordo com a função dada por
P(t) = 4 + 1,5.sen (45°t), sendo o tempo t medido em anos, a
partir de janeiro de 2004. Nessas condições, após 4 anos
dessa data, a população de ovelhas nessa região será igual a
a. 4.000.
b. 4.500.
c. 5.000.
d. 5.500.
e. 6.000.
2.(SENAI 2008) Uma caixa é arrastada por uma corda que
forma 60° com a direção do deslocamento. A força de
tração na corda é de 20 N e a caixa se desloca em 12 m.
1
Dado que cos 60° = , o trabalho da força de tração é, em
2
joules, de
a. 120.
b. 150.
c. 160.
d. 200.
e. 240.
Resumo teórico 48

49. Pré-vestibulinho
Matemática
Tabela Trigonométrica de Ângulos de 1º a 90º
Resumo teórico 49

50. Pré-vestibulinho
Matemática
17. ÁREAS DE FIGURAS PLANAS Paralelogramo
17.1. Área dos principais polígonos
A= b · h
Quadrado
A = lado · lado
A = lado 2 Triângulo
𝐛· 𝐡
A=
𝟐
Retângulo
A= b · h
Círculo
A =  · r2
Losango
𝐃· 𝐝
Coroa Circular
A=
𝟐
A = R2 - r2
A =  (R2 – r2)
Trapézio
Setor Circular
Todo ângulo central determina no círculo uma região
𝐁+𝐛 · 𝐡 chamada circular.
A =
𝟐 Podemos calcular a área A do setor
circular pela regra de três
r2 360º
A n
Resumo teórico 50

51. Pré-vestibulinho
Matemática
Exercícios d) 4,0 m.
e) 3,5 m.
1.(SENAI 2008) Um hotel fazenda dispõe de uma área 3.(SENAI 2008) Uma cafeteira de forma cilíndrica reta,
retangular, medindo 60 m de comprimento e 30 m de medindo 4 cm de raio da base e 20 cm de altura, armazena
largura onde serão construídos três depósitos para 80% de sua capacidade de café. A quantidade de café existente
armazenamento de materiais e um jardim, conforme indica na cafeteira corresponde.a:
a figura: Considere:  = 3.
a) 384 mL.
b) 576 mL.
c) 768 mL.
d) 982 mL.
e) 1.536 mL.
PARA RESPONDER ÀS QUESTÕES 4 E 5,
CONSIDERE O TEXTO E A FIGURA A SEGUIR.
A pipa, também conhecida como papagaio ou
quadrado, foi introduzida no Brasil pelos colonizadores
2
portugueses no século XVI.
Se o jardim deverá ocupar uma área de 120 m , cada Para montar a pipa, representada na figura, foram
armazém terá, em m2, uma área igual a utilizados uma vareta de 40 cm de comprimento, duas
a) 740. varetas de 32 cm de comprimento, tesoura, papel de
b) 720. seda, cola e linha. As varetas são fixadas conforme a fi
c) 680. gura, formando a estrutura da pipa. A linha é passada
d) 600. em todas as pontas da estrutura, e o papel é colado de
e) 560. modo que a extremidade menor da estruturada pipa
fique de fora.
2.(SENAI 2008) Uma roda gigante, de raio 8 m, dista do solo
1,5 m. A roda está girando com três rapazes: João,Paulo e
Francisco. À distância entre João e Francisco é a mesma que
entre Francisco e Paulo, que é a mesma entre João e Paulo,
como mostra a figura:
Dados: sen 30° = 0,5.
cos 30° = 0,87.
tg 30° = 0,58.
4. (Trajano 2007) O comprimento da linha que passa pelos
pontos A, B e C do contorno da estrutura da pipa, em
centímetros, é:
a) 4 (4 + 17).
• d) 18 19. •
b) 2 (8 + 19).
• e) 20 √17 .
•
c) 16 + 17.
5. (Trajano 2007) Na figura, a superfície sombreada
No momento em que Francisco está no ponto mais alto da corresponde ao papel de seda que forma o corpo da pipa. A
roda gigante, a altura de João em relação área dessa superfície sombreada, em centímetros
ao solo é de quadrados, é
a) 5,5 m. (A) 576.
b) 5,0 m. (B) 704.
c) 4,5 m. (C) 832.
Resumo teórico 51

52. Pré-vestibulinho
Matemática
(D) 1 150.
(E) 1 472. São verdadeiras apenas:
a) I e III.
6. (Cotil 2004) Durante anos, uma indústria despejou seus b) II e III.
detritos em uma área de terra demarcada entre os pontos c) III e IV.
representados na figura abaixo. Agora essa área precisa ser d) II, III e IV.
despoluída para a construção do parque aquático “Neto e) I, II e III.
Barreto”. Sabendo que:
5.(PSS-SEE/SP) O tangram é um quebra cabeças chinês
AC = 3 Km muito utilizado pelos professores para desenvolver e/ou
AB=BC=CD=AD = 1,7 Km e aplicar
AC é perpendicular a BD diversos conceitos. Ele é composto de 7 peças e construído
a partir de um quadrado. Sabe-se que a área da
região assinalada (paralelogramo, triângulo menor e
triângulo maior ) é de 28 cm².
2
A área (em km ) a ser despoluída será de:
a) 48
b) 4,8
c) 2,4
d) 24
e) 1,2
7. (Cotil 2005) Segundo repórteres da revista Mundo
Estranho – Especial Olimpíadas 2004, uma piscina olímpica Assim, a área do quadrado maior (composto pelas 7 peças)
faz qualquer piscina de prédio parecer uma banheira metida é
2 2
a besta. E não é só no tamanho que serve de documento: os a) 8cm . d) 32cm .
2 2
blocos de largura têm piso antiderrapante, a água é b) 16cm . e) 64cm .
2
mantida a 27 graus e a divisão entre as raias evita a c) 24cm .
formação de marola. Além disso, fazem parte do show
bandeiras sensores, cordas, juízes. Sabendo que a piscina
2
olímpica possui 150m de perímetro e 1.250 m de área,
quais devem ser as suas dimensões?
a) 40m e 35m
b) 45m e 30m
c) 55m e 20m]
d) 50m e 25m
e) 39m e 36m
8.(PSS-SEE/SP) Observe as afirmações abaixo:
I. Se dobrarmos as dimensões de um reservatório de água
que tem a forma de um cubo, dobramos também o seu
volume.
II. Se dobrarmos as dimensões de um terreno quadrado, sua
área também dobrará.
III. Se dobrarmos as dimensões de um terreno quadrado,
seu perímetro também dobrará.
IV. Se dobrarmos as dimensões de um reservatório de água
que tem a forma de um cubo, o seu volume será
multiplicado por 8.
Resumo teórico 52

53. Pré-vestibulinho
Matemática
18. SÓLIDOS..GEOMÉTRICOS
Volumes de Sólidos
Este tema é complexo para os alunos, uma vez que têm
grande dificuldade em reduzir à mesma unidade de medida,
os valores dados para o cálculo de áreas e volumes. Vai ser
dividido em três partes, na primeira apresenta-se um
Unidades de Volume:
esquema que os alunos podem ter sempre presente, quando
necessitarem de reduzir as unidades de medida . Na
segunda e terceira parte apresentam-se as fórmulas para o
cálculo de áreas e volumes de figuras geométricas mais
utilizadas.
1. Unidades de medida de áreas e de volumes;
2. Áreas de Sólidos;
3. Volumes de Sólidos;
Unidades de Capacidade:
18.1 Unidades de medida de volume;
O cálculo de volumes, os valores dados têm que estar
sempre na mesma unidade de medida e que quando tal não
acontece temos de efetuar a redução à mesma unidade.
Relembrar, como tal se efetuar, recorrendo ao seguinte
esquema:
Unidades de Área:
Quando se calcula a área de uma figura geométrica a sua
unidade de medida aparece sempre ao quadrado (por
exemplo, em metros quadrados).
Unidades agrárias:
Resumo teórico 53

54. Pré-vestibulinho
Matemática
18.2 Volumes de Sólidos;
O cálculo do volume de figuras geométricas,
a) A figura representa tridimensionalmente um prisma reto;
b) O volume de um prisma reto é igual ao produto da área
da base pela altura do sólido, isto é
Exercícios
c) O cubo e o paralelepípedo retângulo são prismas;
d) O volume do cilindro também se pode calcular da mesma 1.(SENAI 2008) Um designer foi contratado por um fabricante
forma que o volume de um prisma reto. de perfumes para projetar uma embalagem do seu novo
perfume que será lançado com o nome de Cleópatra. A
embalagem idealizada pelo designer foi uma pirâmide
Formulário das figuras geométricas 2
quadrangular cuja área da base mede 25 cm . Se o volume da
embalagem deve
3
ser de 50 cm , a altura dessa embalagem deverá medir
Figuras Geométricas: a. 2 cm.
b. 4 cm.
c. 5 cm.
d. 6 cm.
e. 8 cm.
2.(SENAI 2008) Uma companhia de transporte rodoviário
transporta objetos de tamanho tal que a soma de suas
dimensões (comprimento, largura e altura) não exceda a 15 m.
Assim, uma caixa na forma de um cubo cujo volume é 64 m3
a. poderá ser transportada pois a soma de suas dimensões é 16
m.
b. não poderá ser transportada, pois a soma de suas dimensões
é 18 m.
c. poderá ser transportada pois a soma de suas dimensões é 6
m.
Resumo teórico 54

55. Pré-vestibulinho
Matemática
d. não poderá ser transportada, pois a soma de suas dimensões (E) apenas nos pontos médios das arestas do cubo.
é 20 m.
e. poderá ser transportada pois a soma de suas dimensões é 12
m.
3. (TRAJANO 2008) 5.(Trajano 2006)
“ Em 1898, aos 25 anos,
Santos Dumont construiu o
balão “Brasil”, que
apresentava a forma esférica
e sua cor, quase
transparente, se devia à
Para Hagar, a Terra tem a forma de um cubo, porém, na criatividade de Santos
realidade, pode-se considerá-la uma esfera de raio R. Dumont, que adotou a seda
Sabendo-se que o volume de uma esfera de raio R é dado japonesa, mais resistente e
𝟒 mais leve para sua
 r e imaginando-se que a Terra cúbica de Hagar
3
por construção. O balão depois
𝟑
tenha o mesmo volume da Terra real, então a aresta desse de pronto apresentava
cubo, escrita em função de R, é igual a: volume igual a 113 metros
cúbicos de gás hidrogênio e
3 4 área da superfície igual a 113 metros quadrados de seda
a. ( ) . R japonesa”
3
3 4R
b. Marcelo estava lendo o texto anterior sobre a vida e obra
3 de Santos Dumont e questionou: Será que é possível o
número que expressa o volume de um balão ser igual a
3 número que expressa a área da superfície?.
4 Para tirar a dúvida, ele foi pesquisar e descobriu que numa
c. ( )R
3 esfera de raio R, R > 0 o volume é dado por:
2 E a área da superfície e dada por: A = 4  R
2
d. R
3
Logo concluiu que esses números:
4
e. . R a. Nunca podem ser iguais
3 b. Seriam iguais para um único valor de raio
c. Seriam iguais para dois valores distintos de raio
4.(Trajano 2008) A Lei de Gravitação Universal, proposta d. Seriam iguais para três valores distintos de raio
por Isaac Newton, permite dizer que a força de atração e. Seriam iguais para mais de três valores distintos de raio
entre duas massas diminui conforme aumenta a distância
entre elas. Sendo mais preciso, quando aumenta a distância
entre seus centros de massa. Dependendo da geometria do
corpo, o centro de massa coincide com o centro
geométrico.
Considerando o mundo cúbico de Hagar, inclinado
exatamente como o mostrado na tirinha, a força de atração
entre a massa desse mundo e a massa do navio terá maior
intensidade quando o navio estiver situado
(A) na face inferior do cubo.
(B) em qualquer aresta do cubo.
(C) em qualquer vértice do cubo.
(D) no ponto médio da face superior do cubo.
Resumo teórico 55

56. Pré-vestibulinho
Matemática
ordem de escolha não é importante, temos uma
19. Análise combinatória e
combinação de n objetos, tomados p a p.
probabilidade
Exemplo: Combinação de 3 objetos (a, b, c), tomados 2 a 2
(n = 3 e p = 2): ab, ac, bc.
19.2. Princípio fundamental da contagem
Número de combinações de n objetos, tomados k a k:
Se uma tarefa tem k etapas, e cada etapa pode ser
feita de ni maneiras diferentes, então o número total de n n!
alternativas é  
 p  (n  p)! p!
 
n1n2 ... np
19.3. Permutação Exercícios
Considere n objetos diferentes. De quantas 1. Com as letras a, b, c, d, e, f quantos códigos de quatro
maneiras podemos dispor (permutar) esses objetos? letras poderão ser construídos se:
Exemplo: a) nenhuma letra puder ser repetida? R: 360
Objetos a, b, c. Permutações: abc, acb, bac, bca, cab, cba.
b) qualquer letra puder ser repetida qualquer número de
vezes? R: 1.296
Para “n” objetos, o número de permutações é:
Pn = n(n-1)...1 2. Uma urna contém as letras A, A, A, R, R, S. Retira-se letra
por letra, sem reposição. Qual é a probabilidade de sair a
palavra ARARAS? R: 1/60
19.4. Arranjo
3. Ao retirar quatro cartas, ao acaso e sem reposição, de um
Considere n objetos diferentes. De quantas
baralho de 52 cartas, qual é a probabilidade de se obter
maneiras podemos escolher p (p ≤ n) desses objetos? Se a
uma quadra (quatro cartas de mesmo número, uma de cada
ordem de escolha é importante, temos um arranjo de n
naipe)? R: 0,000048
objetos, tomados p a p.
Exemplo: Arranjo de 3 objetos (a, b, c), tomados 2 a 2 (n = 3
e p = 2): ab, ac, ba, bc, ca, cb. 4. Qual é a probabilidade de sair três caras e duas coroas
em cinco lançamentos de uma moeda?R: 5/16
Número de arranjos de n objetos, tomados p a p:
A(n, p) = n(n-1)...(n-k+1) ou
5.Seja um lote com 20 peças, sendo 5 defeituosas. Escolha,
n!
A(n, p)  aleatoriamente, 4 peças do lote (uma amostra aleatória de
(n  p)! quatro peças). Qual é a probabilidade de se obter,
exatamente, duas defeituosas na amostra?R: 0,217
19.5. Combinação
Considere n objetos diferentes. De quantas
maneiras podemos escolher p (p ≤ n) desses objetos? Se a
Resumo teórico 56

57. Pré-vestibulinho
Matemática
6. (Difícil) Numa turma de n alunos, qual é a probabilidade
de haver alguma coincidência de aniversário?
R: A(365, n)
P(coincidênc ia de aniversári o)  1 
365n
7. Com auxílio de uma calculadora científica ou do
computador, faça o exercício 6 para n = 30. R: 0,7063
8.(SENAI 2008) Seis alunos fizeram um trabalho para a
feira de ciências da escola, e dois deles deverão fazer a
apresenta-ção em multimídia. O número de duplas que
poderá ser for-mado para a apresentação
desse trabalho é
a. 15
b. 20
c. 25
d. 30
e. 35
9.(SENAI) Numa partida de futebol, a probabilidade de
1
Francis, o manhoso, ser escalado é de , enquanto
4
que a probabilidade de James, o destemido, ser escalado é
1
de . A probabilidade de apenas um deles ser escalado é
5
1
a.
20
2
b.
9
7
c.
20
11
d.
20
7
e.
9
Resumo teórico 57

58. Pré-vestibulinho
Matemática
20. NOÇÕES DE ESTATÍSTICA 20.3. Representação Gráfica
Dados estatísticos podem ser representados tanto por
20.1. Definição tabelas e por quadros de distribuição por freqüência quanto
por gráficos. O uso gráfico para representar uma situação
estatística pode muitas vezes expor melhor visualmente do
A Estatística trata do conjunto de métodos utilizados
que uma tabela estatística, porém o seu uso deve ser feito
pa-ra obtenção de dados, sua organização em tabelas e
com bastante cautela, utilizando o gráfico adequado em
gráficos e a análise dos dados.
cada situação, veja alguns casos:
Através de análises feitas, a partir dos dados
organizados, podemos, em muitos casos, fazer previsões,
auxiliar na toma- da de desições e, assim, elaborar planos A) Gráfico de Colunas - é um tipo de gráfico muito
mais precisos para chegar a objetivos pretendidos. utiliza-do em diversas situações, indica quantidades,
porcentagens e de fácil comparação entre suas variáveis.
20.2. Conceitos Fundamentais
População e Amostra – Em Estatística ao estudarmos um
conjunto de objetos, de indivíduos ou de ocorrências,
podemos considerar todo o conjunto, chamado de
população, ou parte deste conjunto, chamado de amostra.
Imagine, por exemplo, um campeonato quadrangular entre
Flamengo, Botafogo, Atlético Mineiro e Grêmio, sendo
realizado em um único dia, no Maracanã. Se quisermos
saber qual é a composição da torcida que está no estádio,
podemos desenvolver o estudo
entrevistando:.........................................
▪ o conjunto de todos os torcedores que estão no estádio
(população);
O gráfico acima mostra o desempenho de 3 alunos
▪ ou parte desse conjunto de torcedores (amostra).
durante o ano num determinado curso, pode-se
perfeitamente verifi-car que João teve o melhor
Portanto:
desempenho, seguido de Maria e José teve o pior
desempenho.
População são grupos, geralmente numerosos de mesmas
características que podem ser estudados estatisticamente.
B) Gráfico de Barras – também é um tipo de gráfico
Exemplos: muito utilizado para comparar diversos tipos de dados e é
uma outra variante do gráfico de colunas, sendo
48 alunos que estudam na 5ª série de uma escola; Clubes amplamente utilizado em jornais, revistas,
campeões paulistas de futebol, etc. empresas, etc.
Amostras são partes de grupos de mesmas características,
que geralmente são muito numerosos e que para ser
verificado em sua totalidade seria muito dispendioso.
Exemplos:
10 alunos de uma escola com 995 alunos;
2000 brasileiros ouvidos para uma pesquisa de opinião
política, etc.
O gráfico demonstra a mesma situação do gráfico de
colunas acima, ou seja, as notas de 3 alunos.
Resumo teórico 58

59. Pré-vestibulinho
Matemática
C) Histograma – é um gráfico construído no plano
cartesiano por retângulos em número igual ao número de
classes da distribuição. Cada classe é representada por uma
coluna de altura correspondente a sua freqüência.
Trata-se também de um gráfico de área. É utilizado para
variáveis contínuas, por isso, o gráfico também é contínuo:
as colunas são justapostas. A área de cada coluna é
proporcional à freqüência da classe que representa. Logo, a
área de todo histograma é proporcional à soma total das
freqüências. O gráfico acima mostra a distribuição populacional nas
Para construir um histograma, representamos as classes no grandes metrópoles brasileiras e permite um comparativo
eixo das abscissas de um sistema cartesiano, utilizando entre as quantidades de habitantes existentes em cada
metrópole, sendo que não confunde o leitor e sim permite
segmentos de mesma medida. Para cada um deles,
uma análise mais ampla da situação no momento. Veja
registramos os limites superior e inferior. No ápice do eixo
tabela a seguir, geratriz desse gráfico:
das ordenadas, registramos o maior valor da freqüência,
dividindo o restante proporcionalmente aos outros valores.
REGIÕES METROPOLITANAS POPULAÇÃO PERCENTUAL
Levantamos então as colunas, justapostas.
Grande S.P. (37 municípios) 15.444.900 37,30%
...................................................
Grande R.J. (15 municípios) 9.814.600 23,70%
Grande B.H. (14 municípios) 3.436.100 8,30%
Grande Porto Alegre (14 municípios) 3.026.800 7,30%
Grande Recife (9 municípios) 2.874.500 6,90%
Quantidade de alunos Grande Salvador (8 municípios) 2.496.500 6%
Grande Fortaleza (5 municípios) 2.307.000 5,60%
Grande Curitiba (14 municípios) 2.000.800 4,80%
TOTAL 41.401.200 100%
Outro exemplo: Foi feita uma enquete a 1200 alunos de
uma escola sobre as atividades esportivas que gostariam de
ter na escola. O resultado obtido foi o seguinte:
Atividade Número de
D) Setores – Dos gráficos de Estatística, mais importante Esportiva Alunos
que a contribuição de Descartes foi a doescocês William
Playfair, que trabalhava com estatísticas comerciais. Em Voleibol 600
1786 ele começou a inventar maneiras de representar Basquete 200
dados numéricos por meio de figuras. Uma de suas criações Futebol 100
foram os gráficos de barras ou colunas, como aqueles de Natação 50
João, José e Maria e suas notas bimestrais. Depois de 1801, Outras 250
ele
inventou os gráficos de setores, também chamados de
“tortas” ou “pizzas”. Vejamos um exemplo: Com esses dados pode-se construir uma representação
gráfica de setores dessa distribuição, em que usaremos um
círculo. Lembrando que uma circunferência completa tem
360º, podemos calcular por meio
de uma regra de três simples e direta o ângulo central
correspondente a cada uma das atividades desejadas pelos
alunos.
Assim, temos:
Resumo teórico 59

60. Pré-vestibulinho
Matemática
1200 ------------ 360º à v = 600 x 360º = 180º 2.(SENAI 2008) Segundo dados do IBGE, em 2000, a
600 ------------ v 1200 expectativa de vida para os homens brasileiros era de 64,8
anos. Admitindo que a partir de 2000 a expectativa de vida
1200 ------------ 360º à b = 200 x 360º = 60º dos homens brasileiros esteja aumentando 0,267 anos de
200 ------------ b 1200 vida por ano, pode-se dizer que em 2020 o brasileiro
atingirá a.expectativa de vida ao nascer para os homens de
1200 ------------ 360º à f = 100 x 360º = 30º a. 67,47 anos.
600 ------------ f 1200 b. 68,80 anos.
c. 69,29 anos.
1200 ------------ 360º à n = 50 x 360º = 15º d. 70,14 anos.
50 ------------ n 1200 e. 71,47 anos.
1200 ------------ 360º à o = 250 x 360º = 75º
250 ------------ o 1200
3.(SENAI 2008) Paulo fez uma viagem de automóvel para o
sul do país e levou 8 horas para chegar ao seu destino.
Com essas medidas, poderemos, então construir com o uso O gráfico abaixo mostra a velocidade média do automóvel,
de régua e compasso um gráfico de setores de forma em função do tempo. Lembrando que
correta, utilizando-se de cores e legenda para representar velocidade corresponde a quantos quilômetros foram
melhor a opinião dos alunos quanto ao esporte praticado. percorridos num determinado intervalo de
Veja a construção com o professor. tempo; sabendo que 40 km/h significa que em cada uma
hora foram percorridos 40 km, podemos
dizer que em 5 horas de viagem, Paulo percorreu
20.4. – Medidas de tendência central
Há certas medidas que são típicas numa distribuição: as de
tendência central (médias, medianas) e as de dispersão.
20.4.1. Médias aritméticas
Consideremos, em ordem crescente, um rol de notas
obtidas por alunos de da turma A:
Turma A: 2 3 4 4 5 6 7 7 7 7 8
Sua média aritmética será a soma de todas as notas (60)
dividido pela quantidade de notas (11)
a. 150 km.
2+3+4+4+5+6+7+7+7+7+8 60 b. 250 km.
Média Turma A: =
11 11 c. 350 km.
== 5,45 d. 450 km.
e. 550 km.
A média aritmética da turma A será 5,45
Exercícios
4.(Trajano 2008) Nas Ciências Humanas, a linguagem gráfica
auxilia no entendimento das grandes tendências da
1.(SENAI 2008) Uma avaliação de Matemática foi aplicada em
duas turmas, A e B, da segunda série de uma determinada sociedade, de seu tempo e espaço. Analise o gráfico a
escola. A média das notas dos alunos da turma A foi de 6,0, seguir.
enquanto que na turma B foi de 7,0. Se a turma A possui 30
alunos e a turma B, 20 alunos, a média geral da segunda série
dessa escola será de
a. 6,2
b. 6,3
c. 6,4
d. 6,5
e. 6,6
Resumo teórico 60

61. Pré-vestibulinho
Matemática
construiu-se um gráfico referente aos meios de informação
que levaram os turistas a escolher um desses ambientes
naturais conservados para a sua viagem de férias.
A partir da charge, que ilustra o conflito histórico entre
patrões e empregados,
Analisando o gráfico, pode-se dizer que
(A) mais da metade dos pesquisados obtiveram a
informação por intermédio de amigos ou parentes.
(B) agências de viagens e revistas juntas tiveram,
porcentualmente, mais infl uência na decisão do que a
Internet.
(C) a influência de amigos e parentes é o triplo da influência
e dos dados fornecidos no gráfico, foram feitas as seguintes de publicações especializadas.
afirmações sobre o salário mínimo e a distribuição da renda (D) menos de um quinto dos pesquisados obtiveram
nacional no período 1940-2000. informações via televisão.
(E) a maioria dos pesquisados obtiveram a informação
I. Os trabalhadores de baixa renda obtiveram alguns ganhos
via Internet.
em determinados períodos, mas, sobretudo, acu-
mularam perdas históricas.
6.(Trajano 2008) Pesquisadores descobriram que devido
II. A maior parte da renda nacional historicamente se
ao aquecimento global, os pingüins-reis da Antártida
concentrou entre os mais pobres, sendo eles a maioria
correm o sério risco de virar uma espécie em extinção, já
da população que ganha até 4 salários mínimos.
que, a cada 0,26°C que a temperatura da superfície
III. Em determinados períodos, o salário mínimo tende a marítima sobe, a população adulta deles diminui em 9%.
declinar, em especial quando os trabalhadores são im- Além disso, também notaram que esses animais são
pedidos de lutar e se manifestar, como no período pós- “indicadores sensíveis” das mudanças no ecossistema
1964, durante os regimes militares. marinho e sofrem de forma ampliada os efeitos da
É válido afirmar o contido em mudança climática.
De acordo com estudos, feitos, por meio de marcações
(A) I, II e III.
subcutâneas de identificação eletrônica, percebeu-se
(B) I e II, apenas. que o aumento da temperatura dos mares afeta não só
(C) I e III, apenas. a oferta de alimentos perto da colônia de pingüins-reis
(D) II e III, apenas. das Ilhas Crozet, um arquipélago subantártico, como
(E) II, apenas. interfere no processo de acasalamento das aves.
(Adaptado de: http://www1.folha.uol.com.br/folha/ambiente/ult10007u371815.shtml-
5.(Trajano 2007) Em dezembro de 2002, a Empresa 13/08/2008)
Brasileira de Turismo (EMBRATUR) apresentou um relatório Sobre esse assunto é correto afirmar que
sobre o turismo praticado em ambientes naturais
conservados, que são aqueles que têm garantida a proteção (A) os pingüins, para sobreviverem nas vastas regiões
de seus recursos naturais originais. Para a elaboração do descongeladas da Antártida, se adaptarão variando
relatório, foi feita uma pesquisa com freqüentadores de constantemente a temperatura corporal.
algumas dessas unidades de conservação. Após o
levantamento dos dados,
Resumo teórico 61

62. Pré-vestibulinho
Matemática
(B) os pingüins são dotados de penas, glândulas mamárias,
bico e asas, as quais não servem para voar, mas sim
para nadar, o que favorece a migração no degelo.
(C) as emissões de nitrogênio e enxofre são condições
fundamentais para proteger o continente gelado e a
saúde de todo o planeta.
(D) os pingüins são consumidores primários, e a gordura
subcutânea atua na proteção contra as temperaturas
baixas da água e do vento.
(E) com a mudança de temperatura e salinidade do oceano,
os peixes e os camarões poderão desaparecer, os
pingüins não terão forças para migrar para outras
regiões e provavelmente morrerão de fome.
Resumo teórico 62

63. Pré-vestibulinho
Matemática
A resposta é D. Os outros todos são feitos com linhas retas.
21. Lógica e seqüências
Um círculo é uma linha curva.
21.1. NOÇÕES DE LÓGICA
3. Em algumas questões será pedido para fazer uma
comparação entre palavras.
21.1.1. Sentença ou proposição Exemplo: Qual dos cinco itens faz a melhor comparação?
Barco está para água como avião está para:
SOL - CHÃO - ÁGUA - CÉU - ÁRVORE
Sentença ou proposição é um conjunto de palavras ou
símbolos que exprimem uma idéia. A resposta é céu. Um barco viaja através da água. Isto pode
ser comparado a um avião que viaja pelo céu.
Exemplos:
a) O elefante é um mamífero
4. Em algumas questões será dado um grupo de cinco
b) As árvores falam.
c) Há infinitos números primos. coisas. Quatro delas terão alguma coisa em comum, elas
serão similares de alguma forma. Você será levado a
escolher aquela que não é similar às outras quatro.
21.1.2. Seqüências Exemplo: Qual dos cinco elementos é menos parecido com
os outros quatro?
SEQÜÊNCIAS CÃO - CARRO - GATO - PÁSSARO - PEIXE
A resposta é carro. Os outros são seres vivos. Um carro é
Questões de Amostra: inanimado.
Estude cuidadosamente as seguintes questões de amostra
antes de começar os exercícios. 5. Em algumas questões serão dados números, ou letras, as
quais estarão em uma certa ordem. Eles seguem algum
1. Você terá de fazer comparações entre desenhos.
critério de arranjo. Entretanto, um deles não. Você terá de
Exemplo: Qual dos cinco faz a melhor comparação? escolher aquele que não se encaixa dentro daquele critério.
Exemplo: Qual desses números não pertence à seguinte
série?
1 - 3 - 5 - 7 - 9 - 10 - 11 - 13
A resposta é 10. Começando do 1, os números ímpares são
arranjados em ordem, sendo que 10 não se enquadra nessa
seqüência.
A resposta é C. Um círculo que é dividido em duas partes
pode ser comparado a um quadrado que é dividido em duas 6. Haverá também alguns problemas que você terá de
resolver. Estes não requerem nenhuma matemática difícil.
partes também.
Pelo contrário, eles estarão testando o quão lógico você é,
ou seja, quão bem você pensa.
2. Esta questão também poder vir com desenhos.
OBS: Se uma questão parece ter mais de uma resposta ou
Exemplo: Qual dos cinco desenhos é menos similar aos nenhuma resposta correta, escolha aquela que você
outros quatro? considera ser a melhor dentre as alternativas dadas. Estas
questões são formuladas propositalmente para testar sua
habilidade de pensamento e razão.
Resumo teórico 63

64. Pré-vestibulinho
Matemática
Exercícios sobre Seqüências:
A. Seqüências de Figuras
[1] Escolha a figura correta, dentre as cinco
alternativas colocadas abaixo, para preencher o
espaço do ponto de interrogação:
[3] Qual das imagens abaixo completa melhor a seqüência
superior?
4. Três candidatos a um emprego José, João e Joaquim
submeteram-se a bateria de testes reproduzidas a seguir.
Em todos os testes eles deveriam escolher entre as figuras
enumeradas, aquela que deveria ocupar a vaga assinalada
pelo ponto de interrogação.
[2] Qual das imagens abaixo completa melhor a seqüência
superior?
Resumo teórico 64

65. Pré-vestibulinho
Matemática
5. 7.
6. 8.
7.
9.(Trajano 2007) Um dos passatempos de Júlia é jogar o
sudoku, um quebra-cabeça lógico que virou uma febre
Resumo teórico 65

66. Pré-vestibulinho
Matemática
mundial. Como estratégia para preencher a grade de 10.(Trajano 2008) Considere, da esquerda para a direita, a
sudoku seguinte seqüência de figuras:
a seguir, Júlia começou analisando as possibilidades de
preenchimento da oitava linha e deduziu, corretamente,
qual o número a ser colocado na casa marcadacom a
bolinha preta.
Logo, a próxima figura da seqüência será:
(A)
(B)
(C)
(D)
(E)
O número colocado por Júlia foi
(A) 1.
(B) 4.
(C) 6.
(D) 7.
(E) 9.
Resumo teórico 66

67. Pré-vestibulinho
Matemática
Anexos Eletricidade: Bons e maus condutores de eletricidade.
Eletricidade estática. A corrente elétrica.
Conteúdo Programático Magnetismo: Ímãs e suas propriedades. Magnetismo
terrestre.
Vestibulinho 2010 Propriedades da Matéria: Gerais. Específicas. Mudanças do
estado físico da matéria.
Português
Constituição da Matéria: O átomo. Cargas elétricas. Íons.
Gramática : - Ortografia. Estrutura e formação das palavras. Número atômico e número de massa.
Classes de palavras. Análise sintática do período simples e
composto. Conjunção de verbos regulares e irregulares - Elemento químico: Simbologia e representação. Isótopos,
emprego de tempos e modos. Vozes do verbo. isóbaros e isótonos. Classificação periódica dos elementos:
Concordâncias verbal e nominal. Emprego e colocação dos metais, não metais e gases nobres.
pronomes. Regências verbal e nominal. Figuras de
linguagem. Ligações químicas: Substâncias simples e substâncias
compostas. Ligação iônica e ligação covalente.
Misturas e reações químicas: Processos de separação de
misturas homogêneas e heterogêneas. Reações químicas -
Matemática equação química. Classificação das reações químicas. Lei de
Lavoiser ( conservação das massas). Funções inorgânicas (
Números naturais, inteiros, racionais e irracionais. ácido/base).
Potenciação, radiciação. Expressões algébricas. Produtos
notáveis e fatorações. Razões e proporções. Porcentagem e
Equações de 1º e 2º graus - Problemas de aplicações.
Sistemas de equações de 1º grau. Elementos fundamentais
da geometria plana e semelhança de figuras
planas.Relações métricas no triângulo retângulo.Área de
figuras planas. Noções de estatística. Ciências Biológicas e Programas de
Saúde
Corpo Humano: Organização celular. Organização e
funcionamento dos aparelhos humanos. Órgãos do sentido.
Ciências Físicas Hereditariedade: reprodução e transmissão de
características.
Ar: Massa de ar. Pressão atmosférica. Relação entre pressão
atmosférica e altitude. Programas de saúde: Doenças sexualmente transmissíveis:
contágio, conseqüências e prevenção. Nutrição e
Movimento: Conceito de movimento e repouso. saúde:tipos de alimentos e alimentação equilibrada. O
Características do movimento e repouso. Características do problema das drogas.
movimento uniforme. Características do movimento
uniformemente variado. Seres vivos: Características gerais dos seres vivos: bactérias,
fungos, protozoários, vírus, animais vertebrados e
Força: Medida de força. Diferença entre peso e massa. invertebrados e vegetais superiores.
Forças que se opõem ao movimento. Resultante de sistema
de força. Meio Ambiente: Organização do ecossistema. Relações
ecológicas entre os seres vivos. Interação homem e meio
Energia: Trabalho. Potência. Formas de energia. ambiente: Importância da qualidade da água, tratamento
Transformação de energia. de lixo e esgoto e poluição atmosférica, desmatamento.
Calor: Temperatura e calor. Propagação do calor. Bons e Ciclo biogeoquímicos: Ciclo da água, do oxigênio e do
maus condutores de calor. Dilatação térmica. carbono
Ondas: Propriedades do som. Propagação do som.
Resumo teórico 67