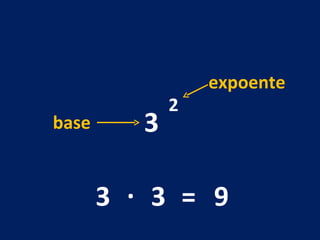
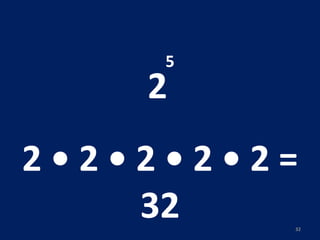
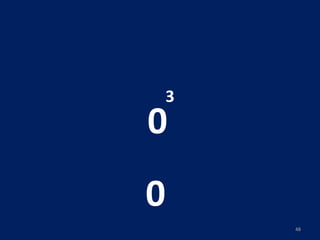
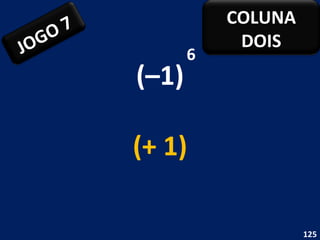
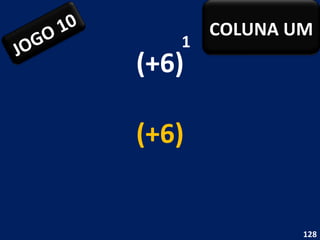
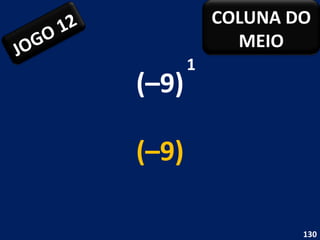
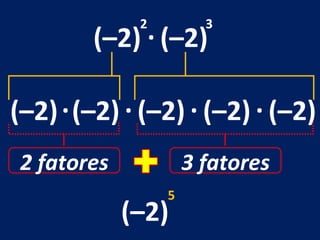
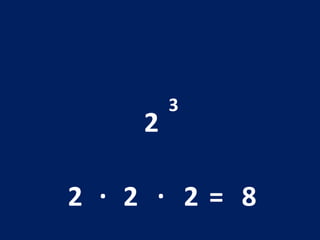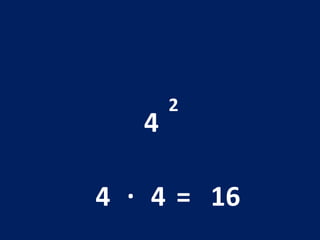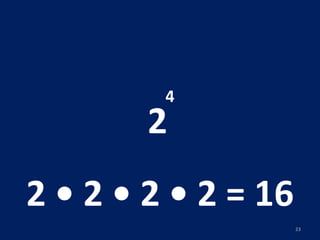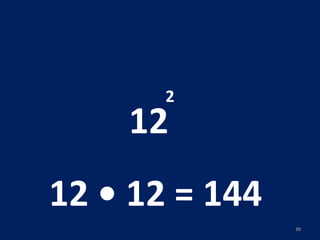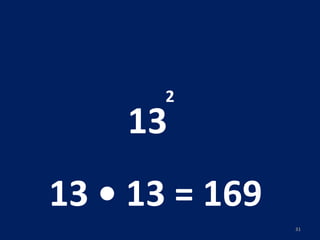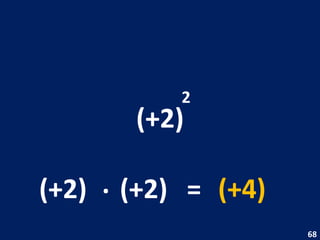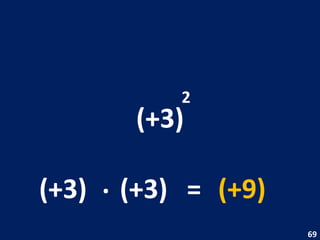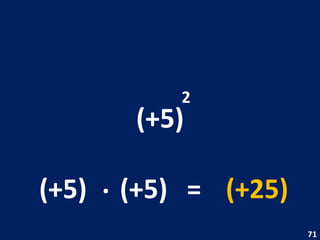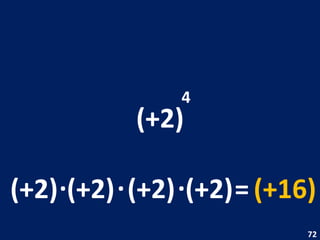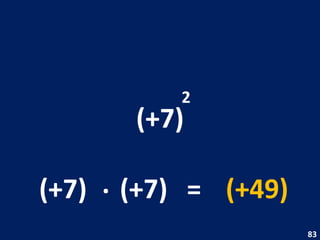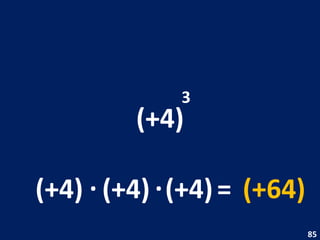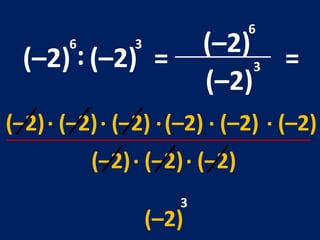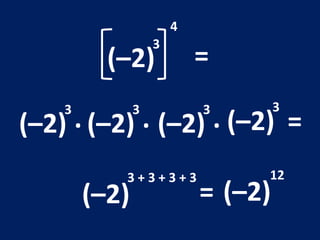O documento discute potenciação de números inteiros, explicando como calcular potências com bases positivas e negativas. É mostrado que quando a base é negativa, se o expoente for par a potência será positiva, e se for ímpar será negativa. Propriedades como produto de potências da mesma base também são abordadas.

1. POTENCIAÇÃO DE NÚMEROS INTEIROS Prof. Materaldo www.matemateens.com.br CEM CENTRO DE ESTUDOS MATEMÁTICOS MAIS DO QUE CÁLCULOS ... AULA 11 7º ANO

2. POTENCIAÇÃO DE NÚMEROS INTEIROS AULA 11

3. O que vimos até aqui?

4. 01 – Sistema de numeração egípcio

5. 02 – Sistema de numeração romano

6. 03 – Sistema de numeração binário

7. 04 – Números inteiros (positivos e negativos)

8. 05 – Adição de números inteiros ( + ) + ( + ) = + ( – ) + ( – ) = – ( + ) + ( – ) = + ou –

9. 06 – Subtração de números inteiros Somar o primeiro com o oposto do segundo

10. ( + ) · ( + ) = ( + ) ( – ) · ( – ) = ( + ) ( + ) · ( – ) = ( – ) ( – ) · ( + ) = ( – ) 07 – Multiplicação de números inteiros

11. 08 – Divisão de números inteiros ( + ) : ( + ) = ( + ) ( – ) : ( – ) = ( + ) ( – ) : ( + ) = ( – ) ( + ) : ( – ) = ( – )

12. 09 – Expressões Numéricas Nas expressões numéricas em que aparecem as operações adição, subtração,multiplicação e divisão devemos efetuá-las nesta ordem: 1º) multiplicações e divisões; 2º) adições algébricas. Sempre na ordem em que aparecem na expressão.

13. 10 – Par ordenado de números inteiros Como um par ordenado indica a localização de determinado ponto, ele também é chamado de coordenadas desse ponto. As retas vermelha e verde são chamadas de eixos.

14. TUNEL DO TEMPO

15. 3 2 3 3 . = 9 expoente base

16. 2 3 2 2 . . 2 = 8

17. 4 2 4 4 . = 16

18. POTÊNCIAS ESPECIAIS 0 = 1 Com expoente zero Com expoente 1 1 = 8 8 7

19. ACERTANDO O ALVO - 24 Potenciação A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br individual

20. É a operação em que, dada uma base e um expoente, se calcula uma potência.

21. 9 2 9 • 9 = 81

22. 3 3 3 • 3 • 3 = 27

23. 2 4 2 • 2 • 2 • 2 = 16

24. 3 4 3 • 3 • 3 • 3 = 81

25. 8 2 8 • 8 = 64

26. 5 3 5 • 5 • 5 = 125

27. 4 3 4 • 4 • 4 = 64

28. 3 5 3 • 3 • 3 • 3 • 3 = 243

29. 18 2 18 • 18 = 324

30. 12 2 12 • 12 = 144

31. 13 2 13 • 13 = 169

32. 2 5 2 • 2 • 2 • 2 • 2 = 32

33. 7 3 7 • 7 • 7 = 343

34. 14 2 14 • 14 = 196

35. 1 3 1 • 1 • 1 = 1

36. 10 3 10 • 10 • 10 = 1.000

37. 15 1 15

38. 3 0 1

39. 0 5 0 • 0 • 0 • 0 • 0 = 0

40. 10 4 10 • 10 • 10 • 10 = 10.000

41. 1 8 1 • 1 • 1 • 1 • 1 • • 1 • 1 • 1 = 1

42. 0 7 0

43. 30 0 1

44. 25 0 1

45. 1 25 1

46. 0 25 0

47. 3 1 3

48. 0 3 0

49. 1 10 1

50. 10 0 1

51. 10 6 1.000.000

52. 1 5 1

53. 5 0 1

54. 10 5 100.000

55. 10 2 10 • 10 = 100 fim

56. POTÊNCIA DE BASE NEGATIVA

57. Para estudar as potências de base negativa, vamos observar a sequência originada de potências.

58. A potência (– 2) origina a sequência: n n 0 1 2 3 ( – 2 ) = 1 0 ( – 2 ) = – 2 1 ( – 2 ) = ( – 2 ) . ( – 2 ) = 4 2 ( – 2 ) = ( – 2 ) . ( – 2 ) . ( – 2 ) = ( – 8 ) 3

59. Potenciação é o produto de fatores iguais, obedecendo às regras de sinais da multiplicação.

60. BASE POSITIVA 3 = 64 ( + 4 ) ( + 4 ) ( + 4 ) ( + 4 ) = . . = 64 base expoente potência

61. QUANDO A BASE É POSITIVA, A POTÊNCIA É SEMPRE POSITIVA 3 = ( + 4 ) base + 64 potência

62. BASE NEGATIVA 3 = – 8 ( – 2 ) ( – 2 ) ( – 2 ) ( – 2 ) = . . = – 8 base expoente potência

63. 2 = + 4 ( – 2 ) ( – 2 ) ( – 2 ) = . = + 4 base expoente potência

64. QUANDO A BASE É NEGATIVA E O EXPOENTE É PAR, A POTÊNCIA É POSITIVA 2 = ( – 2 ) + 4 base expoente potência

65. QUANDO A BASE É NEGATIVA E O EXPOENTE É ÍMPAR, A POTÊNCIA É NEGATIVA 3 = ( – 2 ) – 8 base expoente potência

66. apresenta JORNAL AMAZONÁTICA Um telejornal em defesa do nosso planeta UM BARCO QUE NÃO POLUI

67. ACERTANDO O ALVO - 43 Potenciação de números inteiros A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br individual

68. (+2) 2 (+2) . (+2) = (+4)

69. (+3) 2 (+3) . (+3) = (+9)

70. (+2) 3 (+2) . (+2) = (+8) (+2) .

71. (+5) 2 (+5) . (+5) = (+25)

72. (+2) 4 (+2) . (+2) = (+16) (+2) . (+2) .

73. (+3) 3 (+3) . (+3) = (+27) (+3) .

74. (–2) 2 (– 2) . (– 2) = (+4) Base negativa e expoente par : potência positiva

75. (–2) 4 (–2) . (–2) = (+16) (–2) . (–2) . Base negativa e expoente par : potência positiva

76. (–3) 2 (–3) . (–3) = (+9) Base negativa e expoente par : potência positiva

77. (–5) 2 (–5) . (–5) = (+25) Base negativa e expoente par : potência positiva

78. (–4) 3 (–4) . (–4) = (–64) (–4) . Base negativa e expoente ímpar : potência negativa

79. (–3) 3 (–3) . (–3) = (–27) (–3) . Base negativa e expoente ímpar : potência negativa

80. (–1) 5 (–1) . (–1) = (–1) (–1) . . . (–1) (–1) Base negativa e expoente ímpar : potência negativa

81. (–2) 3 (–2) . (–2) = (–8) (–2) . Base negativa e expoente ímpar : potência negativa

82. (–5) 3 (–5) . (–5) = (–125) (–5) . Base negativa e expoente ímpar : potência negativa

83. (+7) 2 (+7) . (+7) = (+49)

84. (–9) 2 (–9) . (–9) = (+81) Base negativa e expoente par : potência positiva

85. (+4) 3 (+4) . (+4) = (+64) (+4) .

86. (–2) 5 (–2) . (–2) = (–32) (–2) . . . (–2) (–2) Base negativa e expoente ímpar : potência negativa

87. (0) 10 0

88. (–10) 2 (–10) . (–10) = (100) Base negativa e expoente par : potência positiva

89. (–11) 1 (–11) Base negativa e expoente ímpar : potência negativa

90. (+10) 3 (+10) . (+10) = (1000) (+10) .

91. (–10) 3 (–10) . (–10) = (–1000) (–10) . Base negativa e expoente ímpar : potência negativa

92. (+9) 0 1

93. (–1) 6 (+ 1) Base negativa e expoente par : potência positiva

94. (+12) 2 (+12) . (+12) = (144)

95. (–11) 2 (–11) . (–11) = (121) Base negativa e expoente par : potência positiva

96. (–20) 0 1

97. (–1) 5 (–1) . (–1) = (–1) (–1) . . . (–1) (–1) Base negativa e expoente ímpar : potência negativa

98. (+15) 1 15

99. (–15) 1 (–15) Base negativa e expoente ímpar : potência negativa

100. Matema A HISTÓRIA DO NÚMERO UM Parte 4 O Canal de Vídeos da Matemática Tube

101. CALCULANDO 24 Potenciação de números inteiros A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br duplas

102. Escreva na forma de potência (– 15) · (– 15) (– 15) 2

103. Escreva na forma de potência O quadrado de – 5 (– 5) 2

104. Escreva na forma de potência O oposto do quadrado de 5 (– 5) 2

105. Escreva na forma de potência O cubo de – 5 (– 5) 3

106. Escreva na forma de potência – 6 elevado ao expoente zero (– 6) 0

107. Qual é o sinal da potência (– 3) ? negativo ( expoente ímpar) 27

108. Na igualdade (– 1) = – 1 , o expoente pode ser 20? Não, o expoente precisa ser um número ímpar a

109. Qual é o expoente? (– 3) = 81 4 a

110. Qual é o expoente? (+ 5) = 625 4 a

111. Qual é o expoente? (– 6) = – 216 3 a

112. BOLETEENS Informativo do Clube Matemateens ESPAÇO

113. O Universo tem, segundo a astrofísica, mais de 15 bilhões de anos. A grande explosão que teria dado origem ao Universo foi chamada de big-bang.

114. A Via Láctea tem uma extensão aproximada de 100 mil anos-luz (algo em torno de 950 quatrilhões de quilômetros). Os cientistas calculam a existência de mais de 100 bilhões de galáxias como a Via Láctea.

115. A força da gravidade pode nos deixar mais leves ou mais pesados em outras partes do espaço. Veja quanto uma pessoa de 70 quilos pesaria em:

116. Lua 10 Marte 23 Mercúrio 23 Vênus 53 Saturno 64,5 Júpiter 160 Sol 1.680

117. CEM CENTRO DE ESTUDOS MATEMÁTICOS Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br LOTOMÁTICA 75 POTENCIAÇÃO DE NÚMEROS INTEIROS individual

118. CORREÇÃO LOTOMÁTICA 75 POTENCIAÇÃO DE NÚMEROS INTEIROS

119. (+3) 2 (+3) . (+3) = (+9) JOGO 1 COLUNA UM

120. (+5) 3 (+5) . (+5) = (+125) (+5) . JOGO 2 COLUNA DO MEIO

121. (+7) 2 (+7) . (+7) = (+49) JOGO 3 COLUNA DO MEIO

122. (–11) 2 (–11) . (–11) = (121) JOGO 4 COLUNA UM

123. (–5) 3 (–5) . (–5) = (–125) (–5) . JOGO 5 COLUNA DOIS

124. (–3) 4 (–3) . (–3) = (+81) (–3) . (–3) . JOGO 6 COLUNA DO MEIO

125. (–1) 6 (+ 1) JOGO 7 COLUNA DOIS

126. (–2) 8 (+256) JOGO 8 COLUNA UM

127. (– 9) 0 1 JOGO 9 COLUNA DO MEIO

128. (+6) 1 (+6) JOGO 10 COLUNA UM

129. (+31) 0 1 JOGO 11 COLUNA DOIS

130. (–9) 1 (–9) JOGO 12 COLUNA DO MEIO

131. (–4) 3 (–4) . (–4) = (–64) (–4) . JOGO 13 COLUNA UM

132. (–8) 3 (–8) . (–8) = (–512) (–8) . JOGO 14 COLUNA DOIS

133. (+6) 4 (+6) . (+6) = (+1296) (+6) . (+6) . JOGO 15 COLUNA UM

134. Algumas propriedades da potenciação

135. As propriedades válidas para a potenciação de números naturais também valem para a potenciação de números inteiros negativos. Essas propriedades podem auxiliar os cálculos com potências.

136. PRODUTO DE POTÊNCIAS DE MESMA BASE Como escrever na forma de uma só potência? (–2) . (–2) 2 3

137. (–2) . (–2) 2 3 (–2) . (–2) . (–2) . (–2) . (–2) 2 fatores 3 fatores (–2) 5

138. (–2) . (–2) 2 3 PARA MULTIPLICAR POTÊNCIAS DE MESMA BASE, CONSERVAMOS A BASE E SOMAMOS OS EXPOENTES (–2) . (–2) 2 3 = (–2) 2 + 3 = (–2) 5

139. (–5) . (–5) 2 3 (–5) 2 + 3 Reduza a uma única potência = (–5) 5

140. (–2) . (–2) 3 7 (–2) 3 + 7 Reduza a uma única potência = (–2) 10

141. (+3) . (+3) 4 3 (+3) 4 + 3 Reduza a uma única potência = (+3) 7

142. (–4) . (–4) 2 5 (–4) 2 + 5 Reduza a uma única potência = (–4) 7

143. (+7) . (+7) 5 3 (+7) 5 + 3 Reduza a uma única potência = (+7) 8

144. (–2) . (–2) 3 (–2) 3 + 1 Reduza a uma única potência = (–2) 4

145. (+3) . (+3) n m (+3) n + m Reduza a uma única potência = (+3) n + m

146. (–10) . (–10) 5 5 (–10) 5 + 5 Reduza a uma única potência = (–10) 10

147. (–4) . (–4) 3 (–4) 3 + 1 + 4 Reduza a uma única potência = (–4) 8 (–4) 4 .

148. QUOCIENTE DE POTÊNCIAS DE MESMA BASE Como escrever na forma de uma só potência? (–2) : (–2) 6 3

149. (–2) : (–2) 6 3 = (–2) 6 (–2) 3 = (–2) . (–2) (–2) . (–2) . (–2) . (–2) . (–2) . (–2) (–2) . (–2) 3

150. PARA DIVIDIR POTÊNCIAS DE MESMA BASE, NÃO-NULA, CONSERVAMOS A BASE E SUBTRAÍMOS OS EXPOENTES (–2) : (–2) 6 3 = (–2) 6 – 3 = (–2) 3 (–2) : (–2) 6 3

151. (–3) : (–3) 7 5 (–3) 7 – 5 Reduza a uma única potência = (–3) 2

152. (–2) : (–2) 3 2 (–2) 3 – 2 Reduza a uma única potência = (–2)

153. (+7) : (+7) 5 3 (+7) 5 – 3 Reduza a uma única potência = (+7) 2

154. (–5) : (–5) 4 (–5) 4 – 1 Reduza a uma única potência = (–5) 3

155. (–10) : (–10) 9 2 (–10) 9 – 2 Reduza a uma única potência = (–10) 7

156. (–8) : (–8) 3 3 (–8) 3 – 3 Reduza a uma única potência = (–8) 0

157. (+11) : (+11) 2 2 (+11) 2 – 2 Reduza a uma única potência = (+11) 0

158. (+13) : (+13) 4 3 (+13) 4 – 3 Reduza a uma única potência = (+13) 1

159. POTÊNCIA DE UMA POTÊNCIA Como elevar à quarta potência? (–2) 3

160. (–2) 3 4 = . . . = (–2) 3 + 3 + 3 + 3 = (–2) 12 (–2) 3 (–2) 3 (–2) 3 (–2) 3

161. PARA ELEVAR UMA POTÊNCIA A UM EXPOENTE, CONSERVAMOS A BASE E MULTIPLICAMOS OS EXPOENTES (–2) 3 4 (–2) 3 4 (–2) 3 · 4 = (–2) 12 =

162. Reduza a um único expoente (–5) 2 4 (–5) 8

163. Reduza a um único expoente (–3) 3 2 (–3) 6

164. Reduza a um único expoente (+7) 5 2 (+7) 10

165. Reduza a um único expoente (–4) 2 5 (–4) 10

166. Reduza a um único expoente (+9) 5 4 (+9) 20

167. Reduza a um único expoente (–8) 4 3 (–8) 12

168. A nossa diversão é a matemática

169. FRASEANDO - 3 A NOSSA DIVERSÃO É A MATEMÁTICA Prof. Materaldo O conhecimento deve ser disseminado gratuitamente www.matemateens.com.br

170. As palavras estão todas embaralhadas e você deverá colocá-las em ordem, formando, assim, uma definição coerente dos conceitos matemáticos apresentados.

171. QUADRILÁTERO UM QUE TEM APENAS PAR TRAPÉZIO 1 DE LADOS PARALELOS

172. Trapézio Quadrilátero que tem apenas um par de lados paralelos

173. NÚMEROS ADIÇÃO, QUE NUMA ADICIONADOS SÃO PARCELA 2 OS

174. Parcela Numa adição, os números que são adicionados.

175. INGLESA DE DE MEDIDA COMPRIMENTO UNIDADE A 91,4 CM EQUIVALENTE JARDA 3

176. Jarda Unidade inglesa de medida de comprimento equivalente a 91,4 cm

177. SÓLIDO POLÍGONOS CADA UM DOS UM LIMITAM QUE FACE 4

178. Face Cada um dos polígonos que limitam um sólido.

179. UNIDADE DE 1.000 METROS MEDIDA EQUIVALENTE DE A COMPRIMENTO QUILÔMETRO 5

180. Quilômetro Unidade de medida de comprimento equivalente a 1.000 metros

181. 15 QUILOGRAMAS DE MEDIDA EQUIVALENTE MASSA A UNIDADE DE ARROBA 6

182. Arroba Unidade de medida de massa equivalente a 15 quilogramas

183. NÚMERO DE UMA QUANTAS A BASE VEZES POTÊNCIA SE REPETE QUE INDICA EXPOENTE 7

184. Expoente Número que indica quantas vezes a base de uma potência se repete

185. ANTIGA EQUIVALENTE DE UNIDADE DE MEDIDA PÉ 8 A 30,48 CM. INGLESA COMPRIMENTO

186. Pé Antiga unidade inglesa de medida de comprimento equivalente a 30,48 cm.

187. REPRESENTA POR UMA FORMADO PARTE E UMA UM NÚMERO FRAÇÃO MISTA 9 FRACIONÁRIA INTEIRA

188. Fração mista Representa um número formado por uma parte inteira e uma fracionária

189. CONJUNTO NÚMERO ESCREVER POSSIBILITA QUALQUER DE REGRAS QUE E LER SISTEMA DE NUMERAÇÃO 10

190. Sistema de numeração Conjunto de regras que possibilita escrever e ler qualquer número.

191. AUTO AVALIAÇÃO

192. TV MÁTICA O Canal da Matemática Informação é nosso cálculo apresenta

193. PNEUS

194. SUGESTÃO DE LEITURA BIBLIOMÁTICA A BIBLIOTECA DA MATEMÁTICA HISTÓRIA DE SINAIS de Luzia Faraco Ramos Editora Ática Coleção A Descoberta da Matemática

195. Uma carta para... ATIVIDADE EXTRA CLASSE

196. www.matemateens.com.br www.twitter.com/matemateens www.youtube.com/materaldo www.twitter.com/materaldo