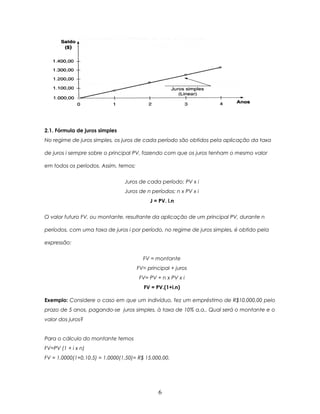
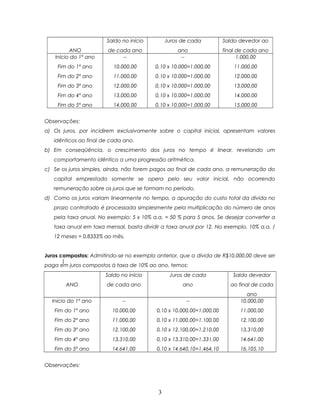
O documento descreve conceitos básicos de matemática financeira, incluindo: 1) Fluxo de caixa é usado para visualizar entradas e saídas de dinheiro ao longo do tempo. 2) Juros simples calculam os juros apenas sobre o capital inicial, enquanto juros compostos incidem juros sobre juros. 3) Fórmulas calculam o valor futuro considerando o capital inicial, taxa de juros e prazo.

1. MATEMÁTICA FINANCEIRA
1. Conceitos Gerais
A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de
investimentos ou financiamentos de bens de consumo.
A Matemática Financeira trata, em essência, do estudo do valor do dinheiro ao longo do
tempo e da existência de juros. O objetivo da matemática financeira é efetuar análises e
comparações de vários fluxos de caixa, de entrada e saída de dinheiro, em diferentes
momentos.
1.1 Diagrama de Fluxo de Caixa
Fluxo de Caixa é o conjunto das entradas e saídas de dinheiro (caixa) ao longo do tempo.
O fluxo de caixa é de grande utilidade para as operações da matemática financeira,
permitindo que se visualize no tempo o que ocorre com o “capital”. Esquematicamente,
pode ser representado da seguinte forma:
A linha horizontal registra a escala de tempo. O ponto zero indica o momento inicial, e os
demais pontos representam os períodos de tempo (datas). As setas para cima indicam
entradas (ou recebimento) de dinheiro, e as setas para baixo indicam saídas (ou
aplicações) de dinheiro. A elaboração do fluxo de caixa é indispensável na análise de
rentabilidades e custos de operações financeiras, e no estudo de viabilidade econômica
de projetos e investimentos. O acompanhamento do fluxo de caixa permite prever os
momentos em que haverá disponibilidade ou falta de recursos.
1.2. Capital e Juro
Capital é qualquer quantidade de dinheiro que esteja disponível em certa data para ser
utilizado numa operação financeira, temporariamente, mediante remuneração. O juro é
a remuneração (o dinheiro) que se paga pelo uso da quantia emprestada, ou o dinheiro
produzido quando o capital é investido.
1

2. 1.3 Principal e Montante
Ao capital inicial empregado dá-se o nome de principal, e a soma do principal mais o juro
recebe o nome de montante.
1.4 Taxa de Juros
Os juros são fixados através de uma taxa percentual que se refere a uma unidade de
tempo: ano, semestre, trimestre, mês, dia.
Exemplos:
a) 8% ao ano = 8% a.a.
b) 4% ao semestre = 4% a.s.
c) 1% ao mês = 1% a.m
As taxas de juros devem ser eficientes de maneira a remunerar:
- o risco envolvido na operação,
- a perda do poder de compra do capital motivada pela inflação,
- o capital emprestado ou aplicado.
A obtenção dos juros do período, em unidades monetárias será feita através da
aplicação da taxa de juros sobre o capital considerado.
Exemplo: Um capital de R$10.000,00 aplicados a uma taxa de 8% ao ano proporcionará,
no final de um ano, um total de juros de: 8% de 10.000 = 0,08 x 10.000 = R$ 800,00.
Observe que a taxa de juros de 8% foi transformada em fração decimal (8/100= 0,08) para
permitir a operação. Assim as taxas de juros terão duas representações:
- Percentagem (para indicar) ; Fração decimal (para efetuar cálculos)
1.5 Regimes de Capitalização
O regime de capitalização de juros é o processo pelo qual os juros são formados e
incorporados ao principal. Podem ser identificados dois regimes de capitalização: juros
simples e juros compostos dependendo do processo de cálculo utilizado.
Exemplo:
Juros simples: Considere o caso em que um indivíduo, fez um empréstimo de R$10.000,00
pelo prazo de 5 anos, pagando-se juros simples, à razão de 10% a.a.. Qual será seu saldo
devedor no final de cada um dos próximos 5 anos?
2

3. Saldo no início Juros de cada Saldo devedor ao
ANO de cada ano ano final de cada ano
Início do 1º ano -- -- 1.000,00
Fim do 1º ano 10.000,00 0,10 x 10.000=1.000,00 11.000,00
Fim do 2º ano 11.000,00 0,10 x 10.000=1.000,00 12.000,00
Fim do 3º ano 12.000,00 0,10 x 10.000=1.000,00 13.000,00
Fim do 4º ano 13.000,00 0,10 x 10.000=1.000,00 14.000,00
Fim do 5º ano 14.000,00 0,10 x 10.000=1.000,00 15.000,00
Observações:
a) Os juros, por incidirem exclusivamente sobre o capital inicial, apresentam valores
idênticos ao final de cada ano.
b) Em conseqüência, o crescimento dos juros no tempo é linear, revelando um
comportamento idêntico a uma progressão aritmética.
c) Se os juros simples, ainda, não forem pagos ao final de cada ano, a remuneração do
capital emprestado somente se opera pelo seu valor inicial, não ocorrendo
remuneração sobre os juros que se formam no período.
d) Como os juros variam linearmente no tempo, a apuração do custo total da dívida no
prazo contratado é processada simplesmente pela multiplicação do número de anos
pela taxa anual. No exemplo: 5 x 10% a.a. = 50 % para 5 anos. Se desejar converter a
taxa anual em taxa mensal, basta dividir a taxa anual por 12. No exemplo, 10% a.a. /
12 meses = 0,8333% ao mês.
Juros compostos: Admitindo-se no exemplo anterior, que a dívida de R$10.000,00 deve ser
paga em juros compostos à taxa de 10% ao ano, temos:
Saldo no início Juros de cada Saldo devedor
ANO de cada ano ano ao final de cada
ano
Início do 1º ano -- -- 10.000,00
Fim do 1º ano 10.000,00 0,10 x 10.000,00=1.000,00 11.000,00
Fim do 2º ano 11.000,00 0,10 x 11.000,00=1.100,00 12.100,00
Fim do 3º ano 12.100,00 0,10 x 12.100,00=1.210,00 13.310,00
Fim do 4º ano 13.310,00 0,10 x 13.310,00=1.331,00 14.641,00
Fim do 5º ano 14.641,00 0,10 x 14.640,10=1.464,10 16.105,10
Observações:
3

4. a) Os juros não incidem unicamente sobre o capital inicial de R$10.000,00, mas sobre o
saldo total existente no início de cada ano. Este saldo incorpora o capital inicial
emprestado mais os juros incorridos em períodos anteriores.
b) O crescimento dos juros se dá em progressão geométrica, evoluindo de forma
exponencial ao longo do tempo.
Em juros simples apenas o principal rende juros, ao passo que a juros compostos os
rendimentos são calculados sobre os montantes, havendo, portanto, uma incidência de
juros sobre juros.
Legalmente deve-se usar o regime de juros simples, mas o mercado financeiro segue
integralmente a lei dos juros compostos. Assim as Letras de Câmbio, os Certificados de
Depósitos Bancários, o Sistema Financeiro de Habitação, as prestações de crediário, os
descontos de duplicatas, e outros intermináveis exemplos do mercado financeiro seguem
a lei dos juros compostos e não a dos juros simples. Entretanto, os juros simples são
utilizados pela facilidade de cálculo, e também como grande argumento de vendas. O
problema é que as contas são feitas a juros simples quando na realidade o fenômeno se
comporta a juros compostos. Assim, por exemplo, uma letra de câmbio com rentabilidade
de 24% ao ano, é dita no mercado como uma letra “2% ao mês”, pois 24% ÷ 12 meses =
2% ao mês, quando realmente a juros compostos, a sua renda mensal é de 1,81% ao mês
(conforme será verificado posteriormente). Evidente que a tarefa de vendas fica
facilitada por essa majoração fictícia da renda mensal do papel. A utilização de
procedimentos semelhantes ao anterior é bastante comum no mercado e cria muitas
dificuldades, pois, o cálculo financeiro correto, sempre se faz a juros compostos, ao passo
que a taxa mencionada na negociação (no exemplo 2%) é, na maioria das vezes, obtida
através de juros simples, fornecendo, portanto, valores inexatos e induzindo a raciocínios
incorretos.
1.6 Simbologia
n prazo ou número de períodos de capitalização de juros, expressos em anos, semestres,
trimestres, meses ou dias.
i taxa de juros por período de capitalização, expressada em porcentagem, e sempre
mencionando a unidade de tempo considerada (ano, semestre, trimestre, mês ou dia).
Sinônimo de rentabilidade.
4

5. PV Valor Presente (Present Value), ou seja, valor do capital inicial (principal) aplicado.
Sinônimo de aplicação, investimento, empréstimo, valor hoje, valor líquido.
FV Valor futuro (Future Value), ou seja, valor do montante acumulado no final de n
períodos de capitalização, com a taxa de juros i. Sinônimo de valor de resgate, valor
nominal, valor em uma data futura.
PMT Valor de cada prestação (Periodic PayMenT).
Observações:
- os intervalos de tempo de todos os períodos são iguais;
- a unidade referencial de tempo da taxa de juros i deve necessariamente coincidir com
a unidade referencial de tempo utilizada para definir o número de períodos n.
- consideraremos para cálculos envolvendo número de dias, o ano comercial que tem
360 dias, e o mês com 30 dias; salvo menção em contrário.
2. JUROS SIMPLES
O regime de juros simples é utilizado no mercado financeiro, notadamente nas operações
de curto prazo, em função da simplicidade de cálculo e também para reduzir ou
aumentar ficticiamente a verdadeira taxa de juros das operações financeiras, o que
facilita a tarefa de colocação dos produtos junto aos investidores ou tomadores de
recursos financeiros.
Em juros simples o crescimento do capital é linear, veja a seguinte tabela:
Ano Saldo Juros do ano Pagamento Saldo final
inicial
1 1.000,00 0,08 x 1.000=80,00 0,00 1.080,00
2 1.080,00 0,08 x 1.000=80,00 0,00 1.160,00
3 1.160,00 0,08 x 1.000=80,00 0,00 1.240,00
4 1.240,00 0,08 x 1.000=80,00 1.320,00 0,00
A representação gráfica dos valores da tabela é mostrada a seguir:
5

6. 2.1. Fórmula de juros simples
No regime de juros simples, os juros de cada período são obtidos pela aplicação da taxa
de juros i sempre sobre o principal PV, fazendo com que os juros tenham o mesmo valor
em todos os períodos. Assim, temos:
Juros de cada período: PV x i
Juros de n períodos: n x PV x i
J = PV. i.n
O valor futuro FV, ou montante, resultante da aplicação de um principal PV, durante n
períodos, com uma taxa de juros i por período, no regime de juros simples, é obtido pela
expressão:
FV = montante
FV= principal + juros
FV= PV + n x PV x i
FV = PV.(1+i.n)
Exemplo: Considere o caso em que um indivíduo, fez um empréstimo de R$10.000,00 pelo
prazo de 5 anos, pagando-se juros simples, à taxa de 10% a.a.. Qual será o montante e o
valor dos juros?
Para o cálculo do montante temos
FV=PV (1 + i x n)
FV = 1.0000(1+0,10.5) = 1.0000(1,50)= R$ 15.000,00.
6

7. Para o cálculo dos juros temos
J = PV. i . n
J = 1.000 x 0,10 x 5 = 500,00.
Logo o montante será R$ 15.000,00 e o valor dos juros de R$ 500,00.
2.2 Juros simples na HP 12C
A calculadora HP 12C opera, basicamente, no regime de juros compostos. No regime de
juros simples a HP 12C calcula o valor dos juros e do montante, com base em uma taxa
anual e um prazo diário.
Digite ou calcule o número de dias e aperte n.
Digite a taxa de juros anual e aperte i.
Digite o valor do principal e aperte CHS PV.
Aperte f INT para calcular o valor dos juros.
Aperte + para calcular o montante.
Observe que em qualquer cálculo financeiro, taxa e prazo devem estar indicados na
mesma unidade referenciais de tempo, porém, no caso da HP 12C, a taxa deve ser anual
e o prazo em dias.
Exemplos:
1. Um amigo lhe empresta R$ 2.000,00 a uma taxa de juros simples de 2% a.m., qual o valor
que você deve pagar a seu amigo após 6 meses?
Pela fórmula:
PV = 5.000,00 FV = PV (1+i.n)
i =2% ao mês = 0,02 FV= 2.000.(1+0,02.6)
n = 6 meses FV = R$ 2.240,00.
Pela HP 12C:
6 ENTER 30 X n
2 ENTER 12 X i
2000 CHS PV
f INT.  R$ 240,00 (valor dos juros)
+  R$ 2.240,00 (valor do montante)
2. Qual deve ser o valor do montante e dos juros ao final de 60 dias de ma aplicação de
R$ 5.000,00 a uma taxa de juros simples de 36% a.a.?
7

8. Pela fórmula:
PV = 5.000 FV = PV (1+i.n)
n = 60 dias FV = 5.000.(1+0,0010.60)
i = 36% ao ano = FV = R$ 5.300,00
36
= %ao dia = 0,10% =0,0010 J =FV –PV = 5.300 – 5.000 = 300,00
360
Pela HP 12C:
60 n
36 i
5000 CHS PV
f INT.  R$ 300,00 (valor dos juros)
+  R$ 5.300,00 (valor do montante)
3. Se um banco remunera suas aplicações a juros simples, qual deverá ser o valor
aplicado hoje, a uma taxa de 2% ao mês para obter R$ 6.000,00 ao final de 1 ano?
Pela fórmula:
PV = ? FV = PV (1+i.n)
n = 1 ano =12 meses 6.000= PV.(1+0,02.12)
i = 2% ao mês = 6.000=PV .1,24
6000
FV = 6.000,00 PV =
1,24
PV = R$ 4.838,71
A HP 12C não realiza o cálculo do capital.
É importante entender que toda operação financeira envolve duas unidades de tempo :
1 - a unidade a que se refere a taxa de juros (ex.: i =12% a.m.)
2 – o prazo de capitalização dos juros (ex.: n = 4 anos).
Essas duas grandezas, para efeito de cálculo, devem estar sempre na mesma unidade de
tempo. Uma sugestão é que se altere sempre o prazo n e evite alterar a taxa i, pois, para
alterarmos i devemos realizar algumas operações que são diretas em juros simples, mas
não em juros compostos.
Relação entre as taxas
i d x 360 = i m x 12 = i b x 6 = i t x 4 =i s x 2 =i a
8

9. onde:
i a = taxa de juros anual
i s = taxa de juros semestral
i t = taxa de juros trimestral
i b = taxa de juros bimestral
i m = taxa de juros mensal
i d = taxa de juros diária.
Exemplos:
1. Para um empréstimo de R$1.000,00 a uma taxa de juros simples de 6% ao semestre
durante 2 anos, qual é o juro capitalizado?
PV = 1.000 PV = 1.000,00
i =6% a.s. = 0,06 ao semestre. i = 6%a.s.= 0,06 x 2 =0,12 ao ano
n = 2 anos = 4 semestres n = 2 anos
J= PV i n = 1.000. 0,06. 4 = R$ 240,00. J= PV.i.n=1.000.0,12.2 = R$ 240,00.
2. Calcular a taxa anual proporcional a 6% ao mês.
i a = i m x12 = 6 x 12 = 72 % a.a.
3. Se a taxa anual é de 30%, qual é a taxa mensal?
i a = i m x12
30 = i m x12
i m = 30 /12
i m = 2,5 % a.m.
Exercícios
1. Determinar o montante acumulado no final de quatro semestres e a renda recebida a
partir da aplicação de um principal de R$10.000,00, com uma taxa de juros de 1% ao mês,
sob o regime de juros simples.
2. Determinar o principal que deve ser aplicado a juros simples, com uma taxa de juros de
10% a.a., para produzir um montante de R$10.000,00 num prazo de 15 meses.
3. Determine os juros acumulados em 3 meses de um capital de R$ 80.000,00 aplicados a
uma taxa de juros simples de 5,5% ao mês.
9

10. 4. Um negociante tomou um empréstimo pagando uma taxa de juros simples de 6% ao
mês durante 9 meses. Ao final desse período, ele pagou R$ 2.700,00 de juros. Determinar o
valor do empréstimo.
5. Um capital de R$ 800,00 foi aplicado num fundo de poupança por11 meses, produzindo
um rendimento de R$ 352,00. Pede-se apurar a taxa de juros oferecida por essa
operação.
6. Uma aplicação de R$ 2.500,00, rendendo a uma taxa de juros de 4,5% ao mês, produz
juros no valor de R$ 675,00. Calcule o prazo da aplicação.
7. Uma pessoa aplica R$1.800,00 à taxa de 8,5% ao mês durante 8 meses. Qual será o
valor do montante ao final desse período?
8. Calcular o montante de um capital de R$ 850.000,00 aplicados no regime de juros
simples por: a) 7 meses a 2,5% a.m.
b) 9 meses a 21,6% a. s.
c) 1 ano e 5 meses a 96% a.a.
9. Determinar os juros e o montante de uma aplicação de R$ 300.000,00 por 19 meses, à
taxa linear (simples) de 42% a.a.
10. Qual capital que produz R$18.000,00 de juros simples, à taxa de 3% a.m. pelo prazo de:
a) 60 dias
b) 80 dias
c) 3 meses e 20 dias
d) 2 anos, 4 meses e 14 dias
11. Uma pessoa aplicou R$ 120.000,00 numa Instituição Financeira resgatando após 7
meses o montante de R$ 160.320,00. Qual a taxa de juros simples mensal que o aplicador
recebeu?
12. O montante de um capital de R$ 6.600,00 ao final de 7 meses é determinado
adicionando-se R$ 5.544,00 de juros. Calcular a taxa linear mensal e anual utilizada.
10

11. 13. Se o valor atual de um título é igual a 4/5 de seu valor e o prazo de aplicação foi de 15
meses, qual a taxa de juros simples considerada?
14. Uma mercadoria é oferecida num magazine por R$1.300,00 à vista, ou nas seguintes
condições: 20% de entrada e um pagamento de R$ 1.069,12 em 30 dias. Calcular a taxa
linear mensal de juros que está sendo cobrada.
15. Em quanto tempo um capital de R$ 400.000,00 aplicados a 64,8% ao ano pelo regime
linear renderá R$ 194.400,00?
16. Uma dívida é composta de 3 pagamentos no valor de R$ 2.800,00, R$ 4.200,00 e R$
7.000,00 vencíveis em 60, 90 e 150 dias respectivamente. Sabe-se ainda que a taxa de
juros de mercado é de 4,5% ao mês. Determinar o valor da dívida se o devedor liquidar os
pagamentos: a) hoje b) daqui a 7 meses.
17. Um negociante tem as seguintes obrigações de pagamento com um banco:
R$18.000,00 vencíveis em 30 dias; R$ 42.000,00 vencíveis em 90 dias; R$10.000,00 vencíveis
em 120 dias. Com problemas de caixa nestas datas deseja substituir este fluxo de
pagamentos pelo seguinte esquema: R$ 20.000,00 em 60 dias; R$ 50.000,00 em 100 dias; o
restante em 150 dias. Sendo de 7,5% ao mês a taxa de juros adotada pelo banco nestas
operações, pede-se calcular o valor do último pagamento.
18. Se a taxa é de 3% a. b., qual é o seu valor mensal, trimestral, semestral e anual?
3. JUROS COMPOSTOS
O regime de juros compostos considera que os juros formados em cada período são
acrescidos ao capital formando o montante do período. Este montante, por sua vez,
passará a render juros no período seguinte formando um novo montante, e assim por
diante. No regime de juros compostos, os juros são capitalizados, produzindo juros sobre
juros periodicamente.
Em juros compostos o crescimento do capital é exponencial, veja a seguinte tabela:
Ano Saldo Juros do ano Pagamento Saldo final
11

12. inicial
1 1.000,00 0,08 x 1.000,00=80,00 0,00 1.080,00
2 1.080,00 0,08 x 1.080,00=86,40 0,00 1.166,40
3 1.166,40 0,08 x 1.166,40=93,31 0,00 1.259,71
4 1.259,71 0,08 x 1.259,71=100,78 1.360,49 0,00
3.1 Fórmulas de Juros Compostos
No regime de juros compostos os juros de cada período são obtidos pela aplicação da
taxa de juros i sobre o capital aplicado no início do período de capitalização. Assim
temos:
a) No 1º período de capitalização (n = 1)
Capital no início do período = PV
Juros do período = PV. i
Capital no final do período = FV = PV + PV. i = PV (1 + i)
b) No 2º período de capitalização (n = 2)
Capital no início do período = PV (1 + i)
Juros do período = PV (1 + i).i
Capital no final do período = FV = PV (1 + i) + PV (1 + i) x i
= PV (1 + i) (1+ i)
= PV (1 + i) 2
c) No 3º período de capitalização (n =3) FV = PV (1 + i)3
d) No enésimo período de capitalização, temos FV = PV (1 + i) n
12

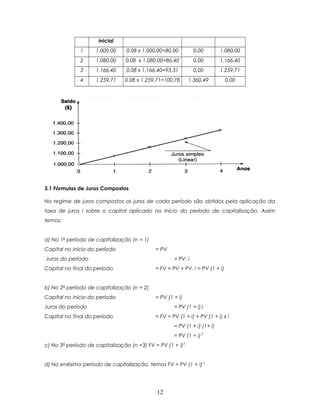
13. Assim, o valor futuro FV, ou montante, resultante da aplicação da aplicação de um
principal PV, durante n períodos de capitalização, com uma taxa de juros i por período,
no regime de juros compostos, é obtido pela expressão:
FV = PV.(1+i)n
Onde a unidade referencial de tempo da taxa de juros i deve coincidir com a unidade
referencial de tempo utilizada para definir o número de períodos n. Em juros compostos
nunca divida ou multiplique a taxa de juros.
Exemplo: Considere o caso em que um indivíduo, fez um empréstimo de R$10.000,00 pelo
prazo de 5 anos, pagando-se juros compostos, à taxa de 10% a.a.. Qual será o montante
e o valor dos juros? Pela fórmula temos que FV = PV (1+i) n = 10.000.(1+0,10)5 = R$ 16.105,10.
As principais fórmulas obtidas de FV = PV(1+i)n são:
FV
- Para calcular o capital PV PV =
(1+ i)n
1
 FV  n
- Para calcular a taxa i i =  −1
 PV 
 FV 
- Para calcular o prazo n n = log  ÷ log(1+ i )
 PV 
- Para calcular o valar dos juros J J = PV.[(1+i)n – 1] ou J = FV – PV
3.2 Juros Compostos na HP 12C
Antes de realizar cálculos de juros compostos com a HP 12C devemos configura-la. Após
a configuração aparecerão alguns indicadores:
Visor Ativar Desativar Função
Indica a opção de cálculo em juros Compostos nas
C STO EEX STO EEX parcelas de períodos não-inteiros
Indica que a série de prestações é calculada
BEG g BEGIN g END antecipada (primeira prestação paga no ato)
As principais funções na HP 12C para juros compostos são: n, i PV, PMT e FV.
Para usá-las, basta digitar os demais valores e solicitar o valor desejado. Antes de cada
novo cálculo devemos limpar a memória da Hp 12C, pressionando as teclas f REG antes
de qualquer operação. Observe que isso limpará o conteúdo de todos os registros da HP
12C. Se quiser apagar apenas os registros financeiros pressione as teclas f FIN.
13

14. Para calcular PV
Digite o prazo e aperte n.
Digite a taxa de juros e aperte i.
Digite o valor futuro e aperte CHS FV.
Aperte PV para calcular o valor presente.
Para calcular FV
Digite o prazo e aperte n .
Digite a taxa de juros e aperte i .
Digite o valor presente e aperte CHS PV.
Aperte FV para calcular o valor futuro.
Para calcular i
Digite o prazo e aperte n .
Digite o valor futuro e aperte FV .
Digite o valor presente e aperte CHS PV.
Aperte i . para calcular a taxa de juros.
Para calcular n
Digite a taxa de juros e aperte i.
Digite o valor presente e aperte PV .
Digite o valor futuro e aperte CHS FV.
Aperte n para calcular o prazo.
Exemplos:
1. Se uma pessoa deseja obter R$ 5.000,00 dentro de um ano, quanto deverá depositar,
hoje, em uma poupança que rende 7% ao mês de juros compostos?
2. Qual é o valor de resgate de uma aplicação de R$ 1.200,00, em um título, pelo prazo
de 8 meses, à taxa de juros composta de 3,5% ao mês?
3. Determinar a taxa de juros mensal composta de uma aplicação de R$ 4.000,00 que
produz um montante de R$ 4.862,00 ao final de um quadrimestre.
14

15. 4. Um empréstimo no valor de R$ 1.300,00 foi liquidado em uma única parcela de R$
1.498,80. A taxa de juros compostos vigente para a operação foi igual a 3,5% a.m. Qual o
prazo da operação?
3.3 Desconto Racional ou “Por Dentro”
Nas operações de desconto racional a taxa incide sobre o valor presente. O valor do
desconto por dentro, expresso em R$, corresponde aos juros acumulados no tempo.
Assim, genericamente, ele pode ser obtido pela diferença entre o valor futuro FV e o valor
presente PV, ou seja:
Desconto = FV – PV
Assim, o valor do desconto “por dentro” (Dd), expresso em R$, é obtido pela expressão
FV[(1+ i)n −1]
Dd = FV – PV =
(1+ i)n
Exemplo: Calcule o desconto de um título de valor nominal igual a R$ 1.000,00
descontado cinco meses antes do seu vencimento a uma taxa de desconto por dentro
de 3% ao mês.
FV[(1+ i)n −1] 1.000[(1 + 0,03) 5 −1]
D= = = R$ 137,39
(1+ i)n (1 + 0,03) 5
5. Desconto Comercial ou “Por Fora”
Nas operações de desconto comercial a taxa incide sobre o valor futuro. O desconto por
fora é aquele que se obtém pelo cálculo do juro sobre o valor nominal do compromisso
que seja saldado em n períodos antes do seu vencimento acrescido de uma taxa
prefixada cobrada sobre o valor nominal.
Os descontos de cada período são obtidos pela aplicação da taxa de desconto d,
sempre sobre o valor futuro FV, fazendo com que os descontos tenham o mesmo valor em
todos os períodos. Assim, o valor líquido é dado por:
PV = FV (1-d)n.
O valor do desconto “por fora” (Df), expresso em R$, é obtido pela aplicação da
expressão:
Df = FV – PV = FV [1-(1-d)n]
15

16. Exemplo: Uma duplicata no valor de R$ 12.000,00 foi descontada cinco meses antes do
vencimento, a uma taxa de desconto por fora igual a 2% ao mês. Calcule o valor líquido
da operação e o valor do desconto.
PV = FV(1-d)n = 12.000.(1-0,02)5 = R$ 10.847,05 é o valor líquido.
D = FV-PV = 12.000 -10.847,05 = R$ 1.152,95 é o valor do desconto.
3.2 Taxas Equivalentes
Taxas equivalentes são taxas de juros fornecidas em unidades de tempo diferentes que ao
serem aplicadas a um mesmo principal durante um mesmo prazo produzem um mesmo
montante acumulado no final daquele prazo, no regime de juros compostos.O conceito
de taxas equivalentes está, portanto, diretamente ligado ao regime de juros compostos.
Assim, a diferença entre taxas equivalentes e taxas proporcionais se prende
exclusivamente ao regime de juros considerado.
Exemplo
Determinar os montantes acumulados no final de quatro anos, a partir de um principal de
$100, no regime de juros compostos, com as seguintes taxas de juros:
(a) 12,6825% ao ano (b)6,1520% ao semestre e (c)1,00% ao mês
6. Fórmulas Relacionando Taxas Equivalentes
Inicialmente, vamos demonstrar a fórmula que relaciona as taxas equivalentes mensal (i m)
e anual (ia). Para isso consideremos as figuras a seguir:
16

17. No regime de juros compostos, a figura referente à taxa mensal, fornece:
(4) FV = PV (1 + im)12
enquanto a figura referente a taxa anual, fornece:
(5) FV = PV (1 + ia)1
Para que essas taxas sejam equivalentes é preciso que os montantes (FV) dos dois
esquemas sejam iguais. Assim, podemos igualar as relações (4) e (5), obtendo:
(1+ im)12 =
(1 + ia)
As demais expressões, relacionando a taxa anual com as taxas equivalentes semestral,
trimestral e diária, podem ser obtidas de maneira análoga. Se considerarmos o ano
comercial (360 dias), as fórmulas que permitem o cálculo dessas taxas equivalentes estão
a seguir indicadas:
(6) (1 + ia) = (1+ is)2 = (1 + it)4 = (1+ im)12 = (1 + id)360
onde:
i a = taxa de juros anual
i s = taxa de juros semestral
i t = taxa de juros trimestral
i m = taxa de juros mensal
i d = taxa de juros diária.
Exemplos
1) Determinar as taxas anual e semestral que são equivalentes à taxa de 1% ao mês.
2) Determinar as taxas anual e semestral que são equivalentes à taxa de 3% a.t.
3) Determinar a taxa mensal que é equivalente à taxa de 10% ao ano.
17

18. No regime de juros compostos, a figura referente à taxa mensal, fornece:
(4) FV = PV (1 + im)12
enquanto a figura referente a taxa anual, fornece:
(5) FV = PV (1 + ia)1
Para que essas taxas sejam equivalentes é preciso que os montantes (FV) dos dois
esquemas sejam iguais. Assim, podemos igualar as relações (4) e (5), obtendo:
(1+ im)12 =
(1 + ia)
As demais expressões, relacionando a taxa anual com as taxas equivalentes semestral,
trimestral e diária, podem ser obtidas de maneira análoga. Se considerarmos o ano
comercial (360 dias), as fórmulas que permitem o cálculo dessas taxas equivalentes estão
a seguir indicadas:
(6) (1 + ia) = (1+ is)2 = (1 + it)4 = (1+ im)12 = (1 + id)360
onde:
i a = taxa de juros anual
i s = taxa de juros semestral
i t = taxa de juros trimestral
i m = taxa de juros mensal
i d = taxa de juros diária.
Exemplos
1) Determinar as taxas anual e semestral que são equivalentes à taxa de 1% ao mês.
2) Determinar as taxas anual e semestral que são equivalentes à taxa de 3% a.t.
3) Determinar a taxa mensal que é equivalente à taxa de 10% ao ano.
17