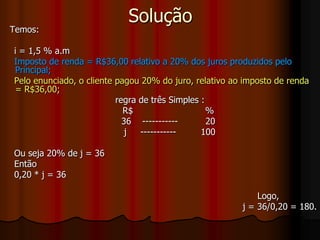
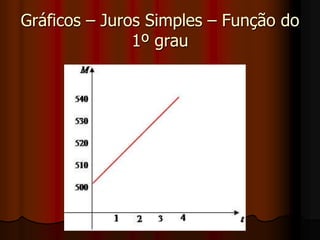
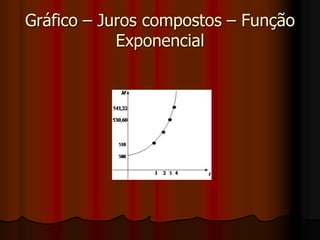
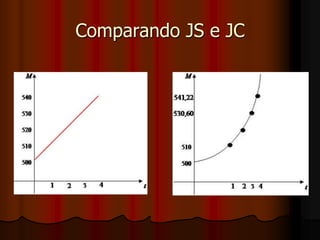
O documento apresenta os conceitos básicos de Matemática Financeira, como juros simples e compostos. Aborda as fórmulas para calcular juros, montante, capital e taxa de juros usando esses dois regimes de capitalização. Também mostra exemplos numéricos de cálculos e gráficos representando a evolução dos montantes ao longo do tempo para juros simples e compostos.

1. IntroduçãoMatemática Financeira:É o ramo da Matemática Aplicada que estuda o comportamento do dinheiro no tempo.Objetivos:1. Quantificar as transações que ocorrem no universo financeiro levando em conta a variável tempo, ou seja o valor monetário no tempo (time value money). 2. As principais variáveis envolvidas no processo de quantificação financeira, são: a taxa de juros, o capital e o tempo.Juros Remuneração de um capital aplicado a uma certa taxa, durante um determinado período, ou seja, é o dinheiro pago pelo uso de dinheiro emprestado. Portanto, Juros (J) preço do crédito.

2. A existência de Juros, decorre de vários fatores, entre os quais destacam-se: 1 - Inflação: a diminuição do poder aquisitivo da moeda num determinado período de tempo.2 - Risco: os juros produzidos de uma certa forma, compensam os possíveis riscos do investimento.3 – Aspectos intrínsecos da natureza humana : os seres humanos adoram ganhar dinheiro!

3. Principais siglas da Matemática Financeira Normalmente o valor do capital é conhecido como principal (P). A taxa de juro (i), é a relação entre os Juros e o Principal, expressa em relação a uma unidade de tempo.

4. Juros Simples Quando a taxa de juros incide no decorrer do tempo, sempre sobre o capital inicial, dizemos que temos um sistema de capitalização simples (Juros simples). Este sistema não é muito utilizado na prática das operações comerciais, mas, a análise desse tema, como introdução à Matemática Financeira, é de uma certa forma bastante interessante.

5. Ilustração A título introdutório, vejamos o seguinte exemplo: Considere que R$100,00 são aplicados à taxa de juros simples de 1% ao mês, durante 3 meses; teríamos neste caso: Juros produzidos ao final do primeiro mês: J = 100.(1%).1 = 100.(1/100) . 1 = R$1,00 Juros produzidos ao final do segundo mês: J = 100.(1%).2 = 100.(1/100) . 2 = R$2,00 Juros produzidos ao final do terceiro mês: J = 100.(1%).3 = 100.(1/100) . 3 = R$3,00

6. Comparando com a fórmula de Juros Simples normalmente conhecida como:J = C * i * t J = 100 * 0,01 * 3 = 3,00sendo a taxa (i) dividida por 100OuJ= P * i * nJ = 100 * 0,01 * 3 = 3,00sendo a taxa (i) dividida por 100

7. Algumas fórmulas derivadas de Juros simplesP = J / i*n  P = 3,00 / 0,01 * 3 = 100i = J / P*n  i = 3,00/100*3 = 0,01*100 = 1 %n = J / P* i  n = 3,00 / 100*0,01 = 3 meses

8. Notas:(a) observe que os juros - neste caso de juros simples - são calculados sempre em relação ao capital inicial de R$100,00.(b) 1 % = 1/100 = 0,01; de uma forma geral, x % = x/100.

9. Conclusão Então, se um capital inicial P for aplicado a juros simples de taxa i por período, durante n períodos e lembrando que os juros simples incidem sempre sobre o capital inicial P, podemos escrever:J = P* i * n onde J = juros produzidos depois de n períodos, do capital P aplicado a uma taxa de juros por período, igual a i.

10. No final de n períodos, é claro que o total será igual ao capital inicial, adicionado aos juros produzidos no período. O capital inicial adicionado aos juros do período é denominadoMONTANTE (M). Logo, teremos: M = P + J (Como J= P*i*n) M = P + P*i*n (colocando P em evidência) M = P(1 + i*n) Portanto, M = P(1+ i*n)

11. Algumas fórmulas derivadas do Montante P = M / 1 + i*ni = M – P/ P * nN = M – P/P * i

12. Exemplos práticos1 - A quantia de R$3.000,00 é aplicada a juros simples de 5% ao mês, durante cinco anos. Calcule o montante ao final dos cinco anos.

13. Solução:Temos: P = 3000;i = 5% = 5/100 = 0,05 e n = 5 anos = 5.12 = 60 meses.Portanto:M = 3000(1 + 0,05.60) = 3000(1+3) = 12000Resposta: R$12000,00

14. 2 - Determine o montante produzido por um capital de R$3000,00 aplicado por 1 mês e dez dias, à taxa de 6% a.b.

15. Solução Temos: P = 3000; i = 6% a.b(ao bimestre) e n = 1 mês e dez dias. Teremos que expressar n e i na mesma unidade de tempo. Vamos referir tudo ao intervalo de tempo em dias, lembrando que nos cálculos comerciais, considera-se 1 mês = 30 dias:

16. a) 1 bimestre = 2 meses = 2.30 = 60 dias. b) 6% a.b = 6% em 60 dias = 6% / 60 = 0,06/60) a.d (ao dia). c) 1 mês e 10 dias = 30 + 10 = 40 dias Agora que está tudo expresso em relação ao mesmo intervalo de tempo, basta aplicar diretamente a fórmula M = P(1 + in), ou seja: M = 3000(1 + (0,06/60).40) M = 3000(1 + 0,04) M = 3000.1,04 = 3120 Resposta: R$3120,00

17. 3 – (Fiscal-MS-2000) Um banco oferece a seus clientes um tipo de aplicação financeira com as seguintes características: Prazo: 4 meses;

18. Remuneração: juros simples à taxa de 1,5% ao mês;

19. Imposto de renda: 20% do juro produzido, pago no final da aplicação.

20. Um cliente pagou R$36,00 de imposto de renda. Seu montante líquido (após o pagamento do imposto de renda) foi:SoluçãoTemos: i = 1,5 % a.mImposto de renda = R$36,00 relativo a 20% dos juros produzidos pelo Principal;Pelo enunciado, o cliente pagou 20% do juro, relativo ao imposto de renda = R$36,00;regra de três Simples : R$ % 36 ----------- 20 j ----------- 100 Ou seja 20% de j = 36 Então 0,20 * j = 36 Logo, j = 36/0,20 = 180.

21. Portanto, os juros da aplicação foram de R$180,00. Como j = P* i * n, substituindo: 180 = P.(1,5/100).4, de onde tiramos P = 3000

22. Aplicando a fórmula do Montante, vem:M = P(1 + in) = M = 3000(1 + (1,5/100).4) M = 3000.1,06 = 3180Mas, deste montante, R$36,00 foram pagos de imposto de renda; logo, o montante procurado é igual a 3180 - 36 = 3144, ou seja, R$3144,00.

23. 4 – (CEF - Técnico Bancário) Um capital foi aplicado a juros simples e, ao completar um período de 1 ano e 4 meses, produziu um montante equivalente a 7/5 do seu valor. A taxa mensal dessa aplicação foi de:

24. Solução: Seja P o capital aplicado durante 1 ano e 4 meses = 12 + 4 = 16 meses, resultando no montante M = (7/5).P Substituindo os valores conhecidos na fórmula de montante M = P(1 + i*n), vem: (7/5)*P = P(1 + i*16)Simplificando P, fica: 1,4 = 1 + 16i ,

25. de onde vem: 0,4 = 16i e finalmente, i = 0,4/16 = 0,025. Para expressar em porcentagem, basta multiplicar por 100 ou seja: i = 0,025.100 = 2,5% a.m.

26. Gráficos das funções envolvendo Montantes As relações envolvendo grandezas são analisadas do ponto de vista das funções matemáticas. As funções possuem inúmeras características e detalham desde cálculos cotidianos até situações de maior complexidade. No caso da Matemática Financeira, as funções são relacionadas às aplicações de capitais nos regimes de juros simples e compostos, os quais utilizamos as funções do 1º grau e exponencial respectivamente. Os gráficos representativos das funções citadas servem de análise sobre o andamento do montante formado mês a mês, observando qual aplicação é mais vantajosa dentro de um determinado período. Observe os gráficos das situações a seguir, eles representarão o andamento da aplicação de acordo com o tipo de capitalização escolhida.

27. Situação – Juros Simples Suponhamos que o capital de R$ 500,00 foi aplicado a uma taxa de 2% ao mês no período de 4 meses, nos regimes de juros simples e compostos. Vamos representar a função de cada aplicação e os gráficos correspondentes aos primeiros meses. Juros simples M = C + j J = C * i * t O Montante ao final do quarto mês será igual a R$ 540,00.

28. Na calculadora financeira HP 12CDigite:500 enter2 enter100 :Enter4 X Enter500 X+  $ 540,00

29. Gráficos – Juros Simples – Função do 1º grau

30. Juros Compostos Quando a taxa de juros incide sobre o capital atualizado com os juros do período (montante), dizemos que temos um sistema de capitalização composta (Juros compostos).

31. Aplicando a mesma situação para juros compostos temos: Juros compostos n M = P * (1 + i) Montante ao final do quarto mês será igual a R$ 541,22

32. NA HP 12 C PELO MÉTODO NORMAL 2 enter100 : enter1 + enter4 Xyenter 500 x

33. Na calculadora Financeira HP 12CDigite:500 PV2 i4 nFV $541,22

34. Gráfico – Juros compostos – Função Exponencial

35. Comparando JS e JC

36. 5 – Um certo capital é aplicado em regime de juros simples, à uma taxa mensal de 5%. Depois de quanto tempo este capital estará duplicado?

37. Solução Temos: M = P(1 + in). Logo, o capital estará duplicado quando M = 2P. Vem:2P = P(1 + 0,05n); (observe que i = 5% a.m. = 5/100 = 0,05). Simplificando P, fica:2 = 1 + 0,05n (2 -1 = 0,05n), então 1 = 0,05n, de onde conclui-se n = 1/0,05 n = 20 meses (1 ano e oito meses).

38. Respostas dos exercícios propostos 1 a 6 1 – Resposta $ 46.000,00 2 - Resposta: 12,5% a.a3 - Resposta: N = 100 dias 4 - Resposta: R$ 36.000,005- Resposta: 20 anos 6 - Resposta: R$6000,00

39. Preparem-se Os exercícios a seguir estão de acordo com os apresentados na aula de hoje, no verso você encontrará as fórmulas para aplicá-las. Tente fazer alguns e nos 10 minutos restantes serão mostrados seus resultados!!! Boa SORTE

40. JUROS SIMPLES1- Qual o valor do juro correspondente a um empréstimo de R$ 3.200,00, pelo prazo de 18 meses, sabendo que a taxa cobrada é de 3% ao mês?2- Calcule o juro simples do capital de R$ 36.000,00, colocado à taxa de 30% ao ano, de 2 de janeiro de 1990 a 28 de maio do mesmo ano.3- Qual a taxa de juro cobrada em um empréstimo de R$ 1.500,00 a ser resgatado por R$ 2.700,00 no final de 2 anos?

41. 4- A que taxa o capital de R$ 24.000,00 rende R$ 1.080,00 em 6 meses?5- Um capital emprestado a 24% ao ano rendeu, em 1 ano, 2 meses e 15 dias, o juro de R$ 7.830,00. Qual foi esse capital?6- Uma aplicação de R$ 400.000,00, pelo prazo de 180 dias, obteve o rendimento de R$ 60.000,00. Qual a taxa anual correspondente a essa aplicação?

42. 7- Em quanto tempo um capital triplica de valor à taxa de 20% ao ano?8- Por quanto tempo um capital deve ser empregado a 40% ao ano para que o juro obtido seja igual a 4/5 do capital?9- Determine o montante de uma aplicação de R$ 5.000,00, à taxa de 2% ao mês, durante 2 anos.10- Sabendo que um capital foi duplicado em 8 anos a juro simples, a que taxa foi empregado esse capital?

43. 11- É mais vantajoso empregar R$ 5.260,00 a 24% ao ano ou R$ 3.510,00 a 22% ao ano e o restante a 28% ao ano?12- Empregam-se 2/3 de um capital a 24% ao ano e o restante a 32% ao ano, obtendo-se, assim, um ganho anual de R$ 8.640,00. Qual é o valor desse capital?13- Determine a aplicação inicial que, à taxa de 27% ao ano, acumulou em 3 anos, 2 meses e 20 dias um montante de R$ 586.432,00.

44. RESPOSTAS1) 1.728,00

45. 2) 4.380,00

46. 3) 40% aa

47. 4) 0,75% am

48. 5) 27.000,00