Juro composto

Capitalização Composta

Taxas de Juros

Matemática Financeira
Prof Eugênio Carlos Stieler

Juro Composto

 Cálculo do rendimento a Juros Compostos:
 Montante;
 Juros;
 Capital;
 Tempo;
 Taxa de juros;
 Equivalência em juros composto.


Juro Composto

 O conceito fundamental de Juros compostos é que
os juros são capitalizados ao longo do período, ou
seja, os juros rendem juros.
 Ex: Um capital de R$ 1.000,00 aplicado por 4 anos a taxa
de 10% ao ano.

Ano (n) 0 1 2 3 4
Juro (j) 0,00 100,00 110,00 121,00 133,10
Montante (S) 1000,00 1100,00 1210,00 1331,00 1464,10


Juro Composto
Montante (taxa 10%a.a.)
300,00
Valores em reais

250,00

200,00

150,00

100,00

50,00

0,00
0 2 4 6 8 10

tempo (anos)


Juro Composto

 Como visto anteriormente, os juros agora são
capitalizados, tornando assim o crescimento
exponencial.
0 1 2 3 n-1 n

j1 = P . i j2 = S1 . i j3 = S2 . i jn-1 = Sn-2 .i jn = Sn-1 . i

S1 = P + j1 => S1 = P (1 + i)
S2 = S1 + j2 => S1 + S1 . i => S1 (1 +i) => P(1+i)(1+i) => P(1+i)2

S3 = S2 + j3 => S2 + S2 . i => S2 (1 +i) => P(1+i)2 (1+i) => P(1+i)3

Sn = Sn-1 + jn => Sn-1 + Sn-1 . i => Sn-1 (1 +i) => P(1+i)n-1 (1+i) => P(1+i)n

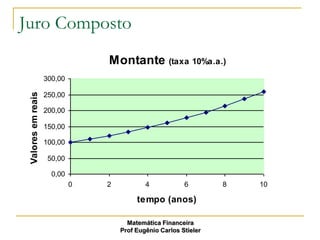
Juro Composto

 Os juros na capitalização composta são
incorporados no capital para novamente serem
calculados

0 1 2 3 n-1 n

Valor Inicial Valor Futuro
ou ou
Principal S = P(1+i)n P = S(1+i)-n Montante
P+J = P(1+i)n S -J= S(1+i)-n
J = P(1+i)n – P J = S – S(1+i)-n
J = P[(1+i)n – 1] J = S[1- (1+i)-n]


Juro Composto

 O Capital representa o valor inicial de um
fluxo de caixa podendo também ser chamado
de:
 Principal
 Valor atual
 Investimento, etc.
0 1 2 3 n-1 n
P S
S = P(1+i)n P = S(1+i)-n

Juro Composto

 A taxa é a razão que remunera o capital em
um determinado período de tempo.
0 1 2 3 n-1 n
P
 Podendo ser constante ou variável ao longo dos
período.

S = P(1+i)n S
S/P = (1+i)n i n 1
P
i = (S/P)1/n -1

Juro Composto

 Prazo, mostra o número de períodos de um
fluxo de caixa completo ou não sendo
dividido em: n
S = P(1+i)
 Meses;
S/P = (1+i)n
 Bimestres;
ln(S/P) = ln(1+i)n
 Semestres;
 Anos, etc ln(S/P) = n.ln(1+i)
S
ln
P
n
ln (1 i)

Juro Composto

 Capitalização Contínua
 Quando a taxa é expressa em um determinado período de
tempo, o cálculo (em princípio) é realizado só no período
que foi estabelecido a taxa, porém em alguns casos há a
necessidade de se reduzir o prazo da taxa. Neste caso se
tivermos a taxa num período de tempo ao dia, será
indiferente receber hoje ou amanhã, chamamos isto de
capitalização contínua.
 Temos então que converter a taxa nominal, para a
equivalente ao dia, isto será demonstrado no próximo
tópico.


Taxas de Juros

 Taxas de juro, vão incidir no cálculo
financeiro, conforme for estabelecido no
problema a ser resolvido. Podem ser
divididas em:
 Proporcionais;
 Nominais
 Equivalentes, e
 Efetivas, real ou capitalizada.


Taxas de Juros

 Proporcionais
 A taxa é expressa em período de tempo, porém em alguns
casos haverá a necessidade de adequação ao período
solicitado. Veja no exemplo abaixo que 2 semestres
correspondem a 1 ano, logo multiplicamos a taxa por dois.
Toda vez que houver a necessidade de conversão, ela
deverá ser feita de forma linear.
Semestres
0 1 2 3 4 5
P S
3% a.s. 3% a.s. 3% a.s. 3% a.s. 3% a.s.

3 x 2 = 6% a.a.

Taxas de Juros

 Nominais
 Corresponde a taxa de um período inteiro como
por exemplo:
Ano 12%
Semestre 6%
Mês 1%

 A conversão é feita de forma linear, ou seja, na
forma da capitalização simples. (proporcional)


Taxas de Juros

 Equivalentes
 Na capitalização composta, todos os valores ao
longo do tempo são capitalizados de forma
exponencial (acumulativa), portanto o mesmo
principio será aplicado na taxa.
 A taxa equivalente corresponde a um valor que é
estabelecido no tempo, e se houver mudança no
período da taxa o resultado não será alterado.
Veja exemplo:


Taxas de Juros

 Exemplo para um período semestral, onde se
deseja converter para anual.
Semestres
0 1 2 3 4 5
P S
5% a.s. 5% a.s. 5% a.s. 5% a.s. 5% a.s.

10,25% a.a.


Taxas de Juros

 Equivalentes
 No exemplo anterior a diferença de valor e justamente
pela acumulação dos juros na forma composta.
 Quando o período da taxa é maior que o período se
deseja descobrir, utilizamos a seguinte formula:
 iq = (1+it)q - 1

 Caso seja o inverso, utilizamos a fórmula:
 iq = (1 + it)1/q – 1
 iq = taxa que quero
 it = taxa que tenho


Taxas de Juros

 Como no dia-a-dia os períodos a que se referem às
taxas que se tem e taxas que se quer são os mais
variados, vamos apresentar uma fórmula genérica,
que possa ser utilizada para qualquer caso, ou seja:
q
t
iq (1 it ) 1
 Para efeito de memorização denominamos as variáveis
como segue:
 iq = taxa para o prazo que eu quero
 it = taxa para o prazo que eu tenho
 q = prazo que eu quero
 t = prazo que eu tenho


Taxas de Juros

 Vejamos alguns exemplos:
 Determinar a taxa para 183 dias, equivalente a
65% ao ano:
 i183 = (1,65)183/360 - 1=28,99%

 Determinar a taxa para 491 dias, equivalente a
5% ao mês:
 i491 = (1,05)491/30 — 1 = 122,23%


Taxas de Juros

 Pontos importantes
 Observar o enunciado da questão a ser resolvida.
Em caso de capitalização simples a conversão
sempre é linear.
 Capitalização composta será utilizada a taxa
equivalente.
 Tudo isto é para adequar o período da taxa com o
período da capitalização.


Bibliografia

 FARO, Clovis de. Fundamentos de Matemática
Financeira. São Paulo: Saraiva, 2006.

 VIEIRA SOBRINHO, José Dutra. Matemática
Financeira. 7ª ed. São Paulo: Atlas, 2000.


Juro composto

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Juro composto

Juro composto