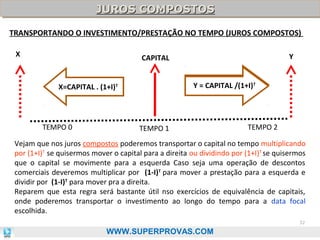
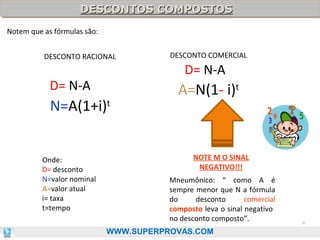
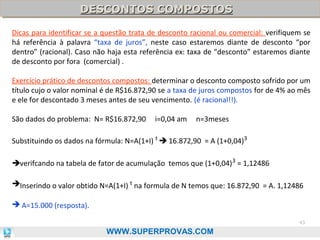
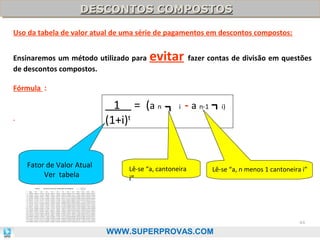
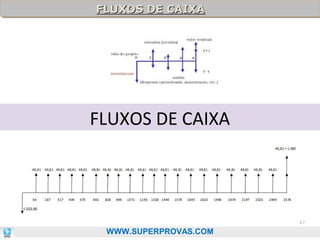
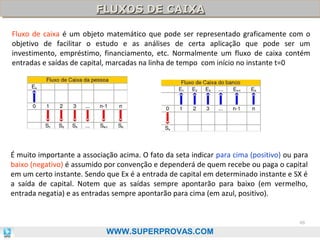
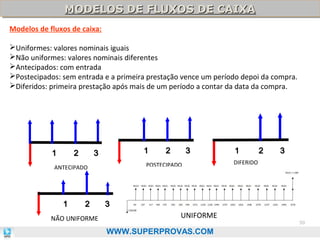
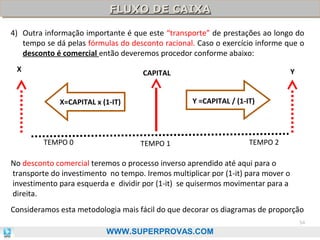
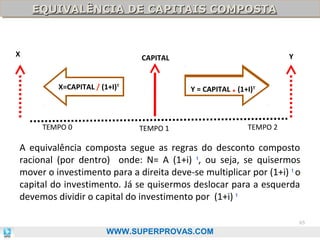
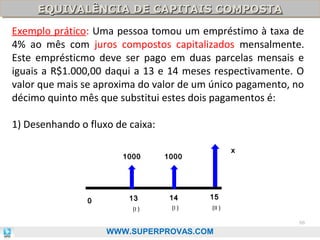
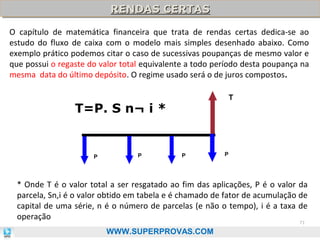
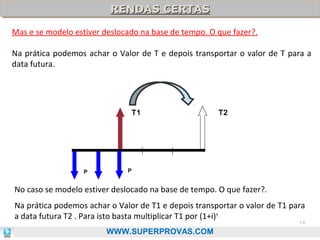
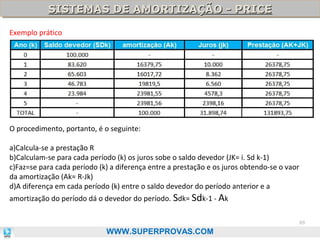
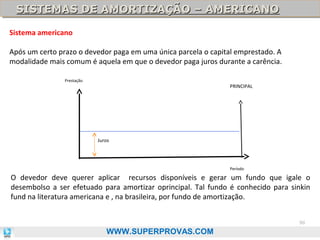
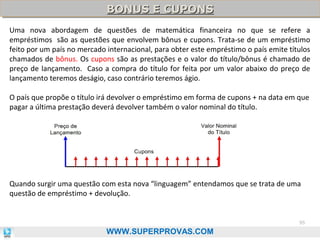
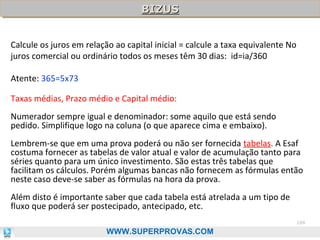
O documento aborda os fundamentos da matemática financeira, focalizando tópicos como juros simples e compostos, descontos, equivalência de capitais, e análise de investimentos. Ele visa oferecer uma visão didática e prática, facilitando a memorização de fórmulas e conceitos através de 'macetes' e exemplos práticos. Além disso, enfatiza a importância de exercícios para a fixação da matéria e o sucesso em provas de concurso.

1. MATEMÁTICA FINANCEIRA
WWW.SUPERPROVAS.COM

2. INTRODUÇÃO
INTRODUÇÃO
ÍNDICE:
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
XIII
XV
XVI
INTRODUÇÃO
Juros simples
Estudo das taxas
Descontos simples
Juros compostos
Descontos compostos
Fluxos de caixa
Equivalência simples
Equivalência composta
Rendas certas
Amortização
Modalidades de amortização
Análise de investimentos
Bônus e cupons
Bizus
pg 3
pg 4
pg 14
pg 19
pg 26
pg 38
pg 47
pg 56
pg 63
pg 70
pg 77
pg 83
pg 91
pg 93
pg 98
2
WWW.SUPERPROVAS.COM

3. INTRODUÇÃO
INTRODUÇÃO
Objetivamos com este resumo fazer uma abordagem básica dos diversos assuntos
que são cobradas pelas bancas examinadoras no que se refere à matéria
“matemática Financeira”. Abordaremos os seguintes assuntos: juros simples,
juros compostos, descontos simples e compostos, equivalência de capitais, rendas
certas e amortizações, fluxo de caixa, bônus e cupons e análise de investimentos.
Falaremos sobre os “macetes” usados para se memorizar as fórmulas, de forma a
ajudar na fixação das mesmas, bem como sua aplicação.
Didática pressupõe “saber explicar na medida certa”. Trabalhamos para expôr os
assuntos na medida certa, sem nos alongarmos em muitos exercícios, para que
haja uma visão geral de forma otimizada. Esperamos ser bem didaticos nas
explicações para que sejam desvendados os segredos da matemática financeira,
bem como sua lógica e macetes.
Aconselhamos, porém, que sejam feitos muitos exercícios nesta matéria, somente
com muitos exercícios o concursando terá condições de enfrentar as questões das
provas. Organizando a teoria de forma objetiva esperamos contribuir para que o
concursando tenha sucesso na fixação da matéria.
3
WWW.SUPERPROVAS.COM

4. JUROS SIMPLES
JUROS SIMPLES
JUROS SIMPLES
4
WWW.SUPERPROVAS.COM

5. JUROS SIMPLES
JUROS SIMPLES
Juros é a remuneração pelo capital aplicado.
JUROS (J)= C.I.T
C= CAPITAL INICIAL
I – TAXA DE JUROS
T = PRAZO DE APLICAÇÃO.
Montante é a soma dos juros mais o capital aplicado
M= C+J*
J= M-C
M=C.(1+I.T)
* SUBSTITUINDO OS JUROS NA FÓRMULA DO MONTANTE TEMOS A FÓRMULA EXPANDIDA DO
MONTANTE
5
WWW.SUPERPROVAS.COM

6. JUROS SIMPLES
JUROS SIMPLES
Representação:
MONTANTE
CAPITAL
0
FLUXO DE CAIXA
T (TEMPO)
6
WWW.SUPERPROVAS.COM

7. JUROS SIMPLES
JUROS SIMPLES
Conceitos iniciais:
Capitalização: operação de adicionar juros ao capital.
Regime de capitalização simples: Os juros são calculados
periodicamente sobre o capital inicial e o montante será a soma do
capital inicial com as parcelas de juros, o que equivale a transformar
o fluxo de caixa com uma única capitalização.
Regime de capitalização composta: Os juros são calculados de
forma cumulativa, ou seja, juros sobre juros, incidindo os juros não
sobre o capital inicial e sim sobre o capital acumulado no período.
Juros comerciais: meses com 30 dias e ano com 360 dias.
Juros exatos: número de dias no mês conforme o calendário e
números de dias no ano correspondentes ao ano civil (365 dias). 7
WWW.SUPERPROVAS.COM

8. JUROS SIMPLES
JUROS SIMPLES
Na matemática financeira deve-se levar em conta o conceito de
“dinheiro no tempo”. Este dinamismo será dado pela “taxa de juros”
Exemplo prático: um capital de R$ 1.000,00 é aplicado a juros
simples durante um período de 3 meses, a uma taxa de 10% ao mês.
Qual o valor a ser resgatado? ( montante).
Pela aplicação da fórmula: M=C (1+ it)
M= 1.000 (1+0,10.3) = 1.300 (resposta).
Notem que taxa e tempo são dados na mesma unidade.
Adotaremos os conceitos de taxas proporcionais nos juros simples
para fazer com que fiquem na mesma unidade.
8
WWW.SUPERPROVAS.COM

9. JUROS SIMPLES
JUROS SIMPLES
TRANSPORTANDO O INVESTIMENTO/PRESTAÇÃO NO TEMPO
X
Y
CAPITAL
Y =CAPITAL X (1+IT)
X=CAPITAL/(1+IT)
TEMPO 0
TEMPO 1
TEMPO 2
Notem a utilidade da fórmula M= C (1+IT), com o uso do (1+IT) podemos transportar o
investimento no tempo. Basta multiplicarmos por (1+IT) se quisermos movimentar para a
direita da base de tempo e dividirmos por (1+IT) se quisermos movimentar o investimento
para a esquerda da base de tempo. Notem que esta regra será usada quando a questão se
referir ao desconto racional somente.
(1+IT) = “FATOR” OU “PARÊNTESES FAMOSO”.
Esta informação será útil nos exercícios de equivalência de capitais.
9
WWW.SUPERPROVAS.COM

10. JUROS SIMPLES
JUROS SIMPLES
TRANSPORTANDO O INVESTIMENTO/PRESTAÇÃO NO TEMPO
X
Y
CAPITAL
Y =CAPITAL / (1- IT)
X=CAPITAL x (1- IT)
TEMPO 0
TEMPO 1
TEMPO 2
Caso haja referência ao desconto comercial na questão o investimento ou prestação
deverá ser transpotado no tempo pela regra inversa: multiplicando o capital por (1-it)
quando movimentar o capital para a esquerda (tempo anterior) edividir o capital por (1- it)
quando movimentar para a diretia (tempo posterior).
Notem que estamos trabalhando com Juros simples. Se forem juros compostos as regras
serão outras.,
10
WWW.SUPERPROVAS.COM

11. JUROS SIMPLES
JUROS SIMPLES
Metodologia de resolução de questões de juros simples pelo
Método gráfico:
MONTANTE
CAPITAL
100
100+ IT
MACETE!!
JUROS
IT
Diagrama de poporcionalidade
O método gráfico consiste em fazer a proporcionalidade entre capital, montante e
juros conforme vemos no diagrama de proporcionalidade acima.
Por este método montamos a figura acima e guardamos as proporcionalidades.
Se o problema for de JUROS e MONTANTE igualamos as proporções respectivas:
JUROS/IT = MONTANTE/100+IT
Já se o problema envolver capital e montante usamos: CAPITAL/100 =
Montante/100+IT
Porém se envolver capital e juros usamos: CAPITAL/100 = JUROS/IT.
WWW.SUPERPROVAS.COM
11

12. JUROS SIMPLES
JUROS SIMPLES
Exemplo prático: o mesmo exercício anterior (que foi resolvido com a aplicação da
fórmula do montante) resolveremos pelo método grafico. Para entender veja diagrama
modelo do slide anterior.
MONTANTE
100+ 30
1000
100
JUROS
30
DIAGRAMA DE PORPORCIONALIDADE NÃO É FLUXO DE CAIXA
Como Capital = 1.000, taxa de juros =30% e tempo = 3 meses inserimos estes valores diretamente na figura modelo e achamos as proporções entre capital e montante (uma única
incógnita que é o montante):
1000 = MONTANTE
100
100+ 30
Resolvendo temos que montante = R$1.300,00.
A vantagem deste método é que com ele torna-se possível levar para a prova as
relações entre juros, montante e capital de forma gráfica e visual.
WWW.SUPERPROVAS.COM
12

13. PREMISSA DA MATEMÁTICA FINANCEIRA
PREMISSA DA MATEMÁTICA FINANCEIRA
A TAXA DE JUROS EM UNIDADE DE TEMPO (EX: 5% AO ANO) E O
TEMPO DEVEM ESTAR SEMPRE NA MESMA UNIDADE!!
Mas e como faremos para converter uma taxa para a mesma unidade de
tempo usada na questão?. Simples!. Usamos o conceito de TAXAS
PROPORCIONAIS (nos juros simples) e de TAXAS EQUIVALENTES * nos juros
compostos!.
*No caso de juros compostos usaremos excepcionalmente o conceito de taxas
proporcionais quando tratamos da convenção linear (juros fracionários).
Notem que podemos também converter o tempo para mesma unidade de
medida de tempo da taxa. Vai depender da questão a escolha de escolha do
valor a ser convertido (tempo ou taxa na medida de tempo ex: tempo em dias e
taxa de 5% ao ano.
Apresentaremos a seguir o conceito de taxas de juros proporcionais x taxas
equivalentes e o conceito de taxas nominais e efetivas.
13
WWW.SUPERPROVAS.COM

14. ESTUDO DAS TAXAS
ESTUDO DAS TAXAS
ESTUDO DAS TAXAS
14
WWW.SUPERPROVAS.COM

15. TAXAS PROPORCIONAIS X TAXAS EQUIVALENTES
TAXAS PROPORCIONAIS X TAXAS EQUIVALENTES
TAXAS PROPORCIONAIS: usamos o conceito de taxas proporcionais quando queremos
converter a taxa de um período de tempo para outro em juros simples.
No caso de conversão da taxa de período menor para maior (taxa ao período)
multiplicamos pelo valor proporcional entre estas medidas de tempo:
Exemplo: 2% ao mês  converter para taxa ao ano.
Usando o conceito de taxas proporcionais temos que:
1 ano tem 12 meses, então multiplicamos por 12:
Calculando temos que 2% ao mês x 12 ´igual a 24% ao ano.
A taxa de 2% ao mês é proporcional à taxa de 24% ao ano!!!!
Já no caso de conversão da taxa de período maior para menor dividimos a taxa em
unidade de tempo pelo valor que representa a proporcionalidade entre estas medidas de
tempo.
Conversões usuais: taxa trimestral para anual (multiplicar por 4 ou dividir por 4 se for de
anual para trimestral), taxa bimestral para anual (multiplicar por 6), taxa semestral para
anual (multiplicar por 2),taxa trimestral para semestral (multiplicar por 2).
15
WWW.SUPERPROVAS.COM

16. TAXAS EFETIVAS X TAXAS NOMINAIS
TAXAS EFETIVAS X TAXAS NOMINAIS
TAXA EQUIVALENTES: veremos quando formos tratar de juros compostos o
conceito de taxas equilvalentes, que nada mais é que que o estudo de uma
fórmula para deixar na mesma base de tempo as taxas igual fazemos com taxas
proporcionais em juros simples.
TAXAS EFETIVAS E TAXAS NOMINAIS: Também os conceitos de taxas efetivas e
taxas nominais serão vistos em juros compostos. Porém adiantamos aqui alguns
conceitos para facilitar a memorização e fixação dos conceitos e denominações
de taxas.
TAXAS NOMINAIS nunca poderão serão aplicadas em fórmulas de juros
compostos. Será sempre necessário convertê-las para TAXAS EFETIVAS.
Exemplo: 10% ao ano capitalizadas semestralmente. Para convertê-las em taxa
efetiva aplica-se o conceito de taxas proporcionais e divide-se 10% por 2
semestres e temos 5% ao semestre que é a taxa equivalente à 10% ao ano
capitalizada semestralmente.
16
WWW.SUPERPROVAS.COM

17. TAXAS APARENTE E TAXA REAL
TAXAS APARENTE E TAXA REAL
TAXA APARENTE : é a taxa com inflação
TAXA REAL: é a taxa sem inflação.
FÓRMULA: TAXA REAL = (1+TAXA APARENTE)/ (1+ INFLAÇÃO)
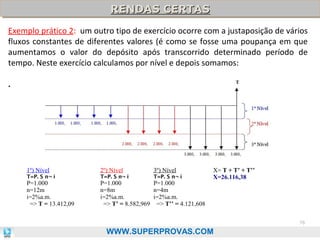
Exemplo: qual o ganho real de um investimento que teve em 2012 um ganho aparente
de 1,44% se a inflação no período foi de 5%?.]
TAXA REAL = (1+0,05)/1+0,10) = 1,2/1,05 = 1,1429
Ou seja: o investimento terá taxa real de 14,29% e uma taxa “aparente” de 20%.
TAXA BRUTA: é a taxa com inclusão dos impostos
TAXA LÍQUIDA: é a taxa sem os impostos
Exemplo prático: se um investimento proporcionou um retorno de 0,9% em um mês,
qual será o seu ganho líquido se considerarmos que foi cobrado 20% sobre o ganho de
imposto de renda?.
Considerando que a taxa de descapitalização relativa aos 20% dos impostos é 0,8 %
então o ganho líquido será 0,9% x 0,8 = 0,72% (resposta).
17
WWW.SUPERPROVAS.COM

18. PRAZO MÉDIO X TAXA MÉDIA X CAPITAL MÉDIO
PRAZO MÉDIO X TAXA MÉDIA X CAPITAL MÉDIO
PRAZO MÉDIO: É a média ponderada dos prazos dos títulos, sendo os pesos iguais aos
valores de cada título
PM= (C1.I1.T1 ) + (C2.I2.T2) + (C3.I3.T3) + (Cn.In.Tn)
(C1.I1) + (C2.I2) + (C2.I3) + (Cn .in)
Sem tempo no denominador
Notem nas fórmulas seguintes que somente o denominador muda e se apresenta sem o
valor que se procura como “médio”. No caso acima está sem o preço no demominador.
TAXA MÉDIA: É a média ponderada das taxas dos títulos
MACETE!!
IM= (C1.I1.T1 ) + (C2.I2.T2) + (C3.I3.T3) + (Cn.In.Tn)
(C1.T1) + (C2.T2) + (C2.T3) + (Cn .Tn)
Sem Taxa no denominador
CAPITAL MÉDIO: É a média ponderada dos capitais.
CM= (C1.I1.T1 ) + (C2.I2.T2) + (C3.I3.T3) + (Cn.In.Tn)
(I1.T1) + (I2.T2) + (I2.T3) + (Cn .in)
Sem capital no denominador
18
WWW.SUPERPROVAS.COM

19. DESCONTOS SIMPLES
DESCONTOS SIMPLES
DESCONTOS SIMPLES
19
WWW.SUPERPROVAS.COM

20. DESCONTOS SIMPLES
DESCONTOS SIMPLES
O QUE SÃO OPERAÇÕES DE DESCONTOS?. Trata-se de operações de antecipação de um
valor que era devido em uma data futura.
VALOR ATUAL: é o valor presente do investimento , ou seja: o valor da data do desconto.
VALOR NOMINAL: é o valor de face ou valor futuro do investimento.
DESCONTO (D) = NOMINAL (N)– ATUAL (A)
N = VALOR NOMINAL
A = VALOR ATUAL
D= N-A
N
A
20
WWW.SUPERPROVAS.COM

21. DESCONTOS SIMPLES
DESCONTOS SIMPLES
DESCONTO RACIONAL – támbém chamado de desconto “por dentro”. O desconto incide
sobre o valor ATUAL do título
DESCONTO COMERCIAL – também chamado de desconto bancário ou “por fora”. O
desconto é calculado sobre o valor nominal do título (valor futuro).
Dentro da Garrafa: Líquido
Fora da Garrafa: Nome
DIAGRAMA DAS PROPORÇÕES
A
N
N
A
100
100+it
100-it
100
Dd
Df
it
it
DESCONTO RACIONAL
MACETE!!
DESCONTO COMERCIAL
21
WWW.SUPERPROVAS.COM

22. DESCONTOS SIMPLES
DESCONTOS SIMPLES
Entendendo o diagrama visual apresentando no slide anterior:
Note que são apenas esquemas mneumônicos e não um fluxo de caixa.
Para memorizar o diagrama basta entender que no desconto incidindo sobre o valor atual
como é o caso do desconto racional, o “100” ficará do lado do atual e
consequentemente dizemos que o valor atual está para 100 e o valor Nominal está para
100 + It
Já se o desconto for comercial, o “100” ficara do lado do Nominal e como o valor
Nominal é sempre maior que o Atual então se o Nominal está para 100, o valor atual está
para (100
Nominal.
- it) = diminuimos o valor de it para que o Atual sempre será menor que
Mneumônico:
MACETE!!
o
Dentro da Garrafa: Líquido
= racional, o desconto é por
dentro e incide sobre o
atual
Fora da garrafa = por fora, o
desconto é comercial e
incide sobre o nominal
22
(nome)
WWW.SUPERPROVAS.COM

23. DESCONTOS SIMPLES
DESCONTOS SIMPLES
1) Fórmulas do desconto simples racional:
A = Dd =
N .
100
It
100+ it
2) Fórmulas do desconto simples comercial:
A = Df = N
100 -it
It
100
MNEUMÔNICO:
DIAGRAMA DAS
PROPORÇÕES
Ver figura do
slide 21
.
Notem que as fórmulas assim podem ser memorizadas observando-se o processo
mneumônico apresentadas anteriormente. Porém também podem ser memorizadas
diretamente pelas fórmulas abaixo (utiliza-se nestes casos os valores unitários das taxas)
1) Fórmula direta do desconto racional :
A=
FORMULAS
DIRETAS
F
N .
1+ it
2) Fórmula direta do desconto comercial:
A = N (1-it)
23
WWW.SUPERPROVAS.COM

24. DESCONTOS SIMPLES
DESCONTOS SIMPLES
Relação entre o Desconto simples por fora (“Dezão”) e o desconto simples por dentro
(“dezinho”).
OBS: usamos esta denominação para ficar mais fácil de decorar e era a didática do
professor “Godinho” em sala de aula.
Regra: o desconto por fora é sempre maior que o desconto por dentro.
Sendo assim: D fora = d dentro (1+it/100) ou didaticamente: D = d (1+it/100)
Poderemos com o uso desta fórmula achar o desconto racional se tivermos já calculado o
desconto comercial, ou vice-versa.
D= d (1+(it/100))
Nota: usem o valor percentual da taxa e não o valor
unitário porque a fórmula já tem o valor 100 para
possibilitar o uso da taxa percentual. (ex:10% = taxa
percentual e 1,10 é a taxa unitária) Usar “10” nesta
fórmula
24
WWW.SUPERPROVAS.COM

25. DESCONTOS SIMPLES
DESCONTOS SIMPLES
RELAÇÃO TAXA POR FORA X TAXA POR DENTRO:
FÓRMULA:
(100/i fora)- (100/i dentro) = n
Onde: ifora= taxa de desconto comercial simples
identro = taxa de desconto racional simples
n= número de períodos de antecipação (igual para os dois tipos de desconto)
Exemplo prático: um título descontado por fora à taxa simples de 10% ao mês é
descontado 3 meses antes do vencimento . Caso fosse usado o desconto simples por dentro
qual seria a taxa de desconto para obter o mesmo desconto?.
(100/ifora)- (100/identro)=n (onde n=3 e Ifora = 10%)
Calculando:
(100/10)- (100/x)=3
-(100/x) = -7
-X=100/7 = 14,29% = esta é a taxa de desconto racional simples encontrada.
WWW.SUPERPROVAS.COM
25

26. JUROS COMPOSTOS
JUROS COMPOSTOS
JUROS COMPOSTOS
WWW.SUPERPROVAS.COM

27. JUROS COMPOSTOS
JUROS COMPOSTOS
Os juros compostos obedecem a uma taxa exponencial - comparando-se com os juros
simples concluímos que nem sempre os juros compostos serão maiores que os juros
simples. Somente serão maiores se o período (n) ou (t) for maior que 1).
Valor Futuro
M=C(1+i) t
Juros simples maiores
que compostos
M=C(1+it)
Juros compostos maiores
que simples
Tempo
Notem que como M=C(1+i) t o componente exponencial “t” for menor que 1 fará com
que o componente “(1+i) t” tenha uma ascendência menor que que o componente
linear da equação (1+it). Porém na medida em que t passa a ser maior que 1 os juros
27
compostos passam a ser maiores que os juros simples.
WWW.SUPERPROVAS.COM

28. JUROS COMPOSTOS
JUROS COMPOSTOS
Equações dos juros compostos: - juros sobre juros:
Onde:
t
I = taxa
M=C(1+i)
M = montante
C = Capital
T = tempo
M=C(1+it)
T
M=C(1+i) t
Juros simples
Juros compostos
Juros por
período
Montante
Juros por
período
Montante
1
1000x0,2=200
1200
100x0,2=200
1200
2
1000x0,2=200
1400
1200 x0,2=240
1440
3
1000x0,2=200
1600
1440x0,2=288
1728
4
1000x0,2=200
1800
1728x0,2=346
2074
Notem que nos juros simples sempre irá incidir a taxa de juros sobre o capital inicial. Já
nos juros compostos será sempre sobre o capital acumulado (montante). Notem também
que no Tempo 1 sempre o valor do montante a juros compostos é igual ao simples.
28
WWW.SUPERPROVAS.COM

29. JUROS COMPOSTOS
JUROS COMPOSTOS
USO DA TABELA PARA OBTER O FATOR DE ACUMULAÇÃO DE CAPITAL EM JUROS
COMPOSTOS.
A equação fundamental dos juros simples é : M=C(1+i) t e como o termos (1+i) t envolve
cálculo de potenciaçção (elevada a potência t) então foi criada a tabela do fator de
acumulação de capital que é justamente o fator (1+i) t para obter o valor deste fator basta
entrar na tabela com o valor de i na horizontal e o valor de tempo navertical. A interseçção
destes valores no meio da tabela será o valor do fator de acumulação de capital (1+i) t
MONTANTE (M)
JUROS
CAPITAL
M=C (1+i) t
J=M-C
29
WWW.SUPERPROVAS.COM

30. TABELA DE ACUMULAÇÃO DE CAPITAL
TABELA DE ACUMULAÇÃO DE CAPITAL
TAXA
TEMPO
Para uma taxa de 8% e tempo =11 temos que (1+i) t = 2,331639
WWW.SUPERPROVAS.COM
30

31. JUROS COMPOSTOS
JUROS COMPOSTOS
TRANSPORTANDO O INVESTIMENTO/PRESTAÇÃO NO TEMPO (JUROS COMPOSTOS)
X
Y
CAPITAL
.
Y = CAPITAL (1+I)TT
Y = CAPITAL (1+I)
X=CAPITAL / (1+I)T
TEMPO 0
TEMPO 1
TEMPO 2
Vejam que nos juros compostos poderemos transportar o capital no tempo
multiplicando por (1+I)T se quisermos mover o capital para a direita ou
dividindo por (1+I)T se quisermos que o capital se movimente para a
esquerda
Reparem que esta regra será bastante útil nso exercícios de equivalência de
capitais, onde poderemos transportar o investimento ao longo do tempo
31
para a data focal escolhida.
WWW.SUPERPROVAS.COM

32. JUROS COMPOSTOS
JUROS COMPOSTOS
TRANSPORTANDO O INVESTIMENTO/PRESTAÇÃO NO TEMPO (JUROS COMPOSTOS)
X
Y
CAPITAL
.
Y CAPITAL (1+I) T
Y ==CAPITAL /(1+I)T
X=CAPITAL . (1+I)T
TEMPO 0
TEMPO 1
TEMPO 2
Vejam que nos juros compostos poderemos transportar o capital no tempo multiplicando
por (1+I)T se quisermos mover o capital para a direita ou dividindo por (1+I)T se quisermos
que o capital se movimente para a esquerda Caso seja uma operação de descontos
comerciais deveremos multiplicar por (1-I)T para mover a prestação para a esquerda e
dividir por (1-I)T para mover pra a direita.
Reparem que esta regra será bastante útil nso exercícios de equivalência de capitais,
onde poderemos transportar o investimento ao longo do tempo para a data focal
escolhida.
32
WWW.SUPERPROVAS.COM

33. TAXAS EQUIVALENTES
TAXAS EQUIVALENTES
FÓRMULA DE CONVERSÃO/MUDANÇA DE BASE DE TEMPO DE TAXAS- CONCEITO DE TAXAS
EQUIVALENTES EM JUROS COMPOSTOS:
Como vimos em juros simples, quando convertemos as bases de tempo das taxas
através do conceito de taxas proporcionais, teremos um conceito semelhante em
juros compostos que é o conceito de “taxas equivalentes” para fazer a conversão
da base de tempo das taxas. Na prática a “fórmula muda”.
A fórmula usada para se obter a taxa equivalente em juros compostos é a
seguinte:
1+I = (1+i) k
Onde: “I”(izão) é a taxa com maior unidade de tempo e “i” (izinho) é a taxa com
menor unidade de tempo. K é qtas vezes a unidade menor cabe dentro da maior33
.
Notem que o K não é tempo e sim um valor obtido de proporcionalidade entre os
WWW.SUPERPROVAS.COM

34. TAXA EQUIVALENTE
TAXA EQUIVALENTE
Exemplo prático: qual a taxa trimestral de juros compostos equivalente à uma taxa
composta de 20% am?
Solução:
1+I = (1+i) t  1+I = (1+0,20) 3
1+I =1.728  I =0,728
I=72.8% ao trimestre
Portanto, a taxa trimestral composta equivalente à 20% ao mês é 72.8% ao
trimestre!.
Nota: no caso para se saber o valor de k devemos fazer a pergunta: quantas vezes o
mês cabe em um trimestre: 3 meses!. Então o k=3. Se fosse bimestre e semestre
faríamos a pergunta: quantas vezes o bimestre cabe dentro do semestre!. E
diríamos: 3 vezes e o K seria 3 também. Lembrar que I = taxa com maior unidade
34
de tempo e i a taxa com menor unidade de tempo.
WWW.SUPERPROVAS.COM

35. TAXAS NOMINAIS E EFETIVAS
TAXAS NOMINAIS E EFETIVAS
Conversão da Taxa Nominal em Taxa Efetiva.
Um problema de juros compostos faz referêcnia a uma taxa de juros de 72% ao
ano capitalizada mensalmente. Qual deverá ser a taxa mensal que usaremos
para calcular o montante?
TAXA NOMINAL: 72% ao ano capitalizada mensalmente tranformamos em
TAXA EFETIVA para saber o valor a ser usado nas fórmulas (taxa ao mês).
Como fazer?  usando o conceito de taxas proporcionais (exceção de uso em
regismes compostos).
Cálculo: se em 12 meses temos 72% de juros
então em 1 mês temos 72/12 = 6% de juros ao mês (taxa efetiva)
Conclusão: a taxa nominal de 72% ao ano corresponde a uma taxa efetiva de
6% ao mês.
35
WWW.SUPERPROVAS.COM

36. TAXAS NOMINAIS E EFETIVAS
TAXAS NOMINAIS E EFETIVAS
Exemplo prático envolvendo os conceitos aprendidos:
Calcular o montante que resultará de um capital de R$ 5.000.00 no fim de 2 anos, aplicada a
juros compostos de 32% ao ano com capitalização trimestral.
Solução: como a capitalização é trimestral, a taxa efetiva, bem como a duração da aplicação
deverão ser indicadas em trimestres.
Taxa efetiva :
Em 12 meses -----------32%
Em 3 meses--------------8%
 taxa efetiva = 8% ao trimestre
Dados: capital= R$ 5.000.00 ; taxa efetiva=8% e período de capitalização =8 trimestres (2
anos) achamos o montante pela fórmula: M=C(1+i) t
M=5.000 (1+0,08) 8 = 5.000. (1.08) 8 = 5.000 x 1.85093 = 9.254,65
Assim, concluímos que o montante procurado é igual a R$ 9.254,65.
Note: o exercício fala em taxa ao ano com capitalização trimestral, neste caso usamos o
conceito de taxas proporcionais. Se não tivesse este nome “ao ano com capitalização
mensal” e quiséssemos converter a taxa de ano para trimestre deveríamos usar o conceito
36
de taxas equivalmentes e usaríamos a fórmula 1+I = (1+i) k
WWW.SUPERPROVAS.COM

37. CONVENÇÃO LINEAR
CONVENÇÃO LINEAR
Se a questão solicitar que se resolva uma questão de juros compostos pelo método linear
deveremos usar a fórmula abaixo, isto somente se a questão solicitar. Trata-se de dar um
tratamento “Linear” à períodos de tempo fracionários ex: 10,5 anos. Pela convenção linear
o tempo 0,5 terá tratamento linear e o tempo “10” (parte inteira do período de tempo) terá
tratamento “exponencial”:
M=C(1+i) INT (1+iQ)
Onde:
M= montante
C = capital
I = taxa composta
INT é a parte interna do tempo
Q é a parte quebrada do tempo
Exemplo prático: considerando que i=10% ao ano, n = 3 anos e 6 meses qual será o
montante calculado pela convenção linear?
R: INT=3 anos e Q = 0,5 anos. Aplicando estes valores na fórmula acima temos:
M=1000 (1+0,10) 3 (1+0,10x0,5) => localizar na tabela o compontente (1+0,10) 3 da fórmula.
Teremos o valor de 1,333.
M=1000 .1,333 (1,05) => 397,55 (resposta).
WWW.SUPERPROVAS.COM
37

38. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
38
WWW.SUPERPROVAS.COM

39. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
O QUE SÃO OPERAÇÕES DE DESCONTOS COMPOSTOS?. Trata-se de operações de
antecipação de um valor que era devido em uma data futura usando a taxa de juros
composta.
VALOR ATUAL (A): é o valor presente do investimento , ou seja: o valor da data do
desconto. Também chamado de valor líquido.
VALOR NOMINAL (N): é o valor de face ou valor futuro do investimento.
DESCONTO (D) = NOMINAL (N)– ATUAL (A)
A = VALOR ATUAL
N = VALOR NOMINAL
D= N-A
N
A
39
WWW.SUPERPROVAS.COM

40. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
DESCONTO RACIONAL – támbém chamado de desconto “por dentro”. O desconto incide
sobre o valor ATUAL do título. (por dentro = lado do atual)
DESCONTO COMERCIAL – também chamado de desconto bancário ou “por fora”. O
desconto é calculado sobre o valor nominal do título (por fora = lado do Nominal).
N
A
N=A(1+i)t
N
A
N OU A? VEJA SEMPRE
O LADO OPOSTO AO
DESCONTO POR FORA
OU POR DENTRO
DESCONTO RACIONAL
A=N(1-i)t
DESCONTO COMERCIAL
A técnica de memorização das fórmulas no desconto composto não envolverá o diagrama
de proporcionalidade usado no desconto simples. No desconto composto trabalharemos
com as dicas para memorização de fórmulas do desconto composto comercial e no
desconto composto racional conforme abaixo:
Desconto composto RIMA COM OPOSTO. E por isto as fórmulas iniciam com a LETRA do
outro lado. Desconto racional é por dentro (lado do Atual), mas a fórmula no desconto
composto irá se iniciar pelo N (letra do lado oposto). Desconto comercial é por fora (lado
do nominal) mas a fórmula irá se iniciar com a letra A (letra do outro lado).
40
WWW.SUPERPROVAS.COM

41. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
Notem que as fórmulas são:
DESCONTO RACIONAL
D= N-A
N=A(1+i)t
Onde:
D= desconto
N=valor nominal
A=valor atual
i= taxa
t=tempo
DESCONTO COMERCIAL
D= N-A
A=N(1- i)t
NOTE M O SINAL
NEGATIVO!!!
Mneumônico: “ como A é
sempre menor que N a fórmula
do
desconto
comercial
composto leva o sinal negativo
no desconto composto”.
WWW.SUPERPROVAS.COM
e

42. TABELA DE ACUMULAÇÃO DE CAPITAL
TABELA DE ACUMULAÇÃO DE CAPITAL
TAXA
Usaremos no desconto composto a tabela de
acumulação de capital para determinar valores de
(1+i)t
TEMPO
Para uma taxa de 8% e tempo =11 temos que (1+i) t = 2,331639
WWW.SUPERPROVAS.COM
42

43. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
Dicas para identificar se a questão trata de desconto racional ou comercial: verifiquem se
há referência à palavra “taxa de juros”, neste caso estaremos diante de desconto “por
dentro” (racional). Caso não haja esta referência ex: taxa de “desconto” estaremos diante
de desconto por fora (comercial) .
Exercício prático de descontos compostos: determinar o desconto composto sofrido por um
título cujo o valor nominal é de R$16.872,90 se a taxa de juros compostos for de 4% ao mês
e ele for descontado 3 meses antes de seu vencimento. (é racional!!).
São dados do problema: N= R$16.872,90
i=0,04 am
n=3meses
Substituindo os dados na fórmula: N=A(1+I) t  16.872,90 = A (1+0,04)3
verifcando na tabela de fator de acumulação temos que (1+0,04) 3 = 1,12486
Inserindo o valor obtido N=A(1+I) t na formula de N temos que: 16.872,90 = A. 1,12486
 A=15.000 (resposta).
43
WWW.SUPERPROVAS.COM

44. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
Uso da tabela de valor atual de uma série de pagamentos em descontos compostos:
Ensinaremos um método utilizado para
de descontos compostos.
evitar fazer contas de divisão em questões
Fórmula :
1 = (a n
(1+i)t
Fator de Valor Atual
Ver tabela
i
- a n-1
Lê-se “a, cantoneira
i”
i)
Lê-se “a, n menos 1 cantoneira i”
44
WWW.SUPERPROVAS.COM

45. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
TABELA DE FATOR DE VALOR ATUAL DE UMA SÉRIE DE PAGAMENTOS:
Usamos a fórmula abaixo para evitar que fazer divisões demoradas na realização de
exercícios:
1 = (a n
(1+i)t
i
- a n-1
i)
MACETE!!
Exemplo prático: um titulo com valor de face R$ 1.000.000,00 foi descontado um mês
antes de seu vencimento. Calcule o valor pago considerando um desconto racional
composto a taxa de 8% ao mês.
Resposta: como o desconto é comercial a fórmula inicia com N teremos que: N= A(1+i) t e
como o valor pedido é o atual teremos que A = 1000/(1+8%) 1  jogando na fórmula
acima temos que:
A= 1000 * = 1000 x (a 1
8% - a 0 8%)  na tabela para n=1 mês e n-1=0 temos:
(1+8%)t
A = 1000 ( 0,925926 – 0)
A= R$ 925.926,00 (*obtido sem ter que resolver esta divisão )
WWW.SUPERPROVAS.COM
45

46. DESCONTOS COMPOSTOS
DESCONTOS COMPOSTOS
TABELA DE FATOR DE VALOR ATUAL DE UMA SÉRIE DE PAGAMENTOS:
Usaremos no desconto composto a tabela de série de pagamentos para determinar valores de 1/ (1+i) t pois:
1 = (a n ,i - a n-1, i) c conforme demonstrado no slide anterior.
(1+i)t
46
WWW.SUPERPROVAS.COM

47. FLUXOS DE CAIXA
FLUXOS DE CAIXA
FLUXOS DE CAIXA
47
WWW.SUPERPROVAS.COM

48. FLUXOS DE CAIXA
FLUXOS DE CAIXA
Fluxo de caixa é um objeto matemático que pode ser representado graficamente com o
objetivo de facilitar o estudo e as análises de certa aplicação que pode ser um
investimento, empréstimo, financiamento, etc. Normalmente um fluxo de caixa contém
entradas e saídas de capital, marcadas na linha de tempo com início no instante t=0
É muito importante a associação acima. O fato da seta indicar para cima (positivo) ou para
baixo (negativo) é assumido por convenção e dependerá de quem recebe ou paga o capital
em um certo instante. Sendo que Ex é a entrada de capital em determinado instante e SX é
a saída de capital. Notem que as saídas sempre apontarão para baixo (em vermelho,
entrada negatia) e as entradas sempre apontarão para cima (em azul, positivo).
48
WWW.SUPERPROVAS.COM

49. FLUXO DE CAIXA
FLUXO DE CAIXA
Exemplo da representação de um fluxo de caixa:
Um investidor aplicou hoje R$ 200,00 por um mês, planejando resgatar R$250,00. Desenhe
o diagrama de fluxo de caixa da operação.
250.00
1
meses
-200.00
A convenção do fluxo é
da contabilidade do
investidor.
Note: não confundir o fluxo de caixa com o diagrama de
proporcionalidade visto em descontos simples. Neste último caso não há
fluxos positivos e negativos e é somente uma diagrama mneumônico
para lembrar das fórmulas.
49
WWW.SUPERPROVAS.COM

50. MODELOS DE FLUXOS DE CAIXA
MODELOS DE FLUXOS DE CAIXA
Modelos de fluxos de caixa:
Uniformes: valores nominais iguais
Não uniformes: valores nominais diferentes
Antecipados: com entrada
Postecipados: sem entrada e a primeira prestação vence um período depoi da compra.
Diferidos: primeira prestação após mais de um período a contar da data da compra.
1
2
1
3
2
NÃO UNIFORME
3
POSTECIPADO
ANTECIPADO
1
2
1
2
3
DIFERIDO
3
UNIFORME
WWW.SUPERPROVAS.COM
50

51. FLUXO DE CAIXA
FLUXO DE CAIXA
Exemplo da representação de um fluxo de caixa (modelo básico)
O modelo básico de um fluxo de caixa pode ser calculado pela fórmula abaixo:
(1 + i ) n − 1
a n ,i =
n
i (1 + i )
VP = an,i.PMT
PMT = VALOR DA PRESTAÇÃO
0
1
2
3
4
Acharemos os valores de pagamentos pela divisão PMT= VP/an,i sendo que an,i é obtido na tabela já
apresentada de valor atual de uma série de pagamentos.
Cada modelo terá uma fórmula. Apresentamos a fórmula mais simples. Será útil este recurso para
podermos tranformar uma série de pagamentos em um único pagamento. Este modelo não tem
prazo de carência e a primeira prestação é paga um período após a compra.
Com base nesta teoria inicial ficaá mais fácil entender “Rendas Certas” apresentada nos próximos
slides.
51
WWW.SUPERPROVAS.COM

52. FLUXO DE CAIXA
FLUXO DE CAIXA
Fixando os conceitos aprendidos atá aqui:
1)Caso
trabalhemos com descontos simples usaremos o diagrama de
proporcionalidades para decorar as fórmulas tanto no desconto racional quanto
no comercial
2)Caso trabalhemos com descontos compostos seguiremos as regras para decorar
as formulas basendo-se na frase “composto rima com oposto”. Desta forma se o
desconto for racional (por dentro) a fórmula começará pela letra do lado oposto
(por fora, ou seja a fórmula irá se iniciar pela letra N (nominal) = ). Já se o
desconto for comercial (por fora) e lembrando da frase composto rima com
oposto a fórmula irá começar com “A=...” e terá sinal de menos.
3)Podemos transportar um determinado investimento ou prestação no tempo
(matemática financeira trabalha com dinheiro no tempo). O fator (1+ it) servirá
para isto, na medida em que se o investimento for multiplicado pelo fator ele se
move para a direita e se for dividido pelo fator o investimento irá movido para a
esquerda. Isto no desconto simples. ´No composto o fator é
(1+ i) t e seguirá os mesmos princípios.
52
WWW.SUPERPROVAS.COM

53. FLUXO DE CAIXA
FLUXO DE CAIXA
4) No caso de termos um fluxo de investimentos (vários investimentos) usaremos as
tabelas e as fórmulas apresentandas que serão definidas conforme o diagrama
de fluxo de caixa conforme detalhamos a seguir.
5) No modelo básico de fluxo em que não há antecipação (entrada) e que não há
carência, ou seja, a primeira prestação inicia-se no primeiro período posterior à
compra usamos a fórmula abaixo (ou a tabela correspondente) para se
determinar o valor correspondente ao fluxo que será transportado para o início
do fluxo determinando o valor atual, ou valor presente de uma série de
pagamentos (na data focal zero).
(1 + i ) n − 1
a n ,i =
n
i (1 + i )
VP =
an,i.PMT
6) Já o valor futuro de uma série de pagamentos será visto posteriormente em
rendas certas. O importante é saber que estes fluxos seguem modelos
matemáticos que irá transformá-los em um valor de um único invesimento que
irá representar todo o título, através de seu valor atual (caso queiramos
transportar a série de investimentos para o início do fluxo ou através de seu valor
futuro caso queiramos tranportar a série de investimentos para o fim do fluxo de
53
caixa.
WWW.SUPERPROVAS.COM

54. FLUXO DE CAIXA
FLUXO DE CAIXA
4) Outra informação importante é que este “transporte” de prestações ao longo do
tempo se dá pelas fórmulas do desconto racional. Caso o exercício informe que o
desconto é comercial então deveremos procedor conforme abaixo:
X
Y
CAPITAL
Y =CAPITAL / (1-IT)
X=CAPITAL x (1-IT)
TEMPO 0
TEMPO 1
TEMPO 2
No desconto comercial teremos o processo inverso aprendido até aqui para o
transporte do investimento no tempo. Iremos multiplicar por (1-it) para mover o
investimento para esquerda e dividir por (1-it) se quisermos movimentar para a
direita.
Consideramos esta metodologia mais fácil do que decorar os diagramas de proporção
54
WWW.SUPERPROVAS.COM

55. FLUXO DE CAIXA
FLUXO DE CAIXA
4) Não esquecer da fórmula de desconto (D=N-A) , pois esta é uma
fórmula básica mas que ajudará bastante na resolução das
questões, uma vez que sabendo os valores de duas das
incógnitas descobriremos facilmente a terceira incógnita desta
fórmula.
5) Atenção especial aos macetes que evitam as divisões na
resolução dos exercícios. Em uma prova em que o tempo vale
ouro é preciso fazer cálculos rápidos que evitem a divisão.
Apresentamos no desconto composto uma maneira mais ágil de
se resolver questões em que temos estas divisões através do uso
de tabelas de valor atual.
6) Notem que as mesmas regras que são válidas para transporte de
investimentos no tempo podem ser usadas para as prestações.
55
WWW.SUPERPROVAS.COM

56. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
56
WWW.SUPERPROVAS.COM

57. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
O que significa Equivalência de capitais?
Definição: dois capitais, representados por papéis ou títulos financeiros são
equivalentes para uma determinada data, sujeitos à juros simples, se os valores
atuais , nesta data (data zero ou focal) forem iguais.
Qual a utilidade dos conceitos que envolvem equivalência de capitais?.
Uma utilidade prática de entender os conceitos referentes à equivalência de
capitais é a renegociação de dívidas. Apresentaremos nos próximos slides um
exemplo prático.
Como resolver um problema envolvendo equivalência de capitais?.
Descreveremos na sequência os passos necessários para se resolver um problema
de equivalência de capitais, lembrando que as questões de equivalência de
capital serão resolvidos SEMPRE atrávés de operações de desconto. E por isto
devemos identificar o tipo de desconto utilizado na questão para que possamos
“transportar” os investimentos para a DATA FOCAL.
57
WWW.SUPERPROVAS.COM

58. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
Passos para resolver uma questão de equivalência de capitais:
1) Primeiro é necessáro “desenhar” o fluxo de caixa correspondente
2) Verificar qual o regime utilizado e o tipo do desconto. E a data focal.
Lembrando que taxa e tempo devem estar na mesma unidade.,
3) Após a verificação anterior, fazemos o transporte de cada investimento para a
data focal usando as regras de “transporte” de investimentos ao longo do tempo
ou as regras de desconto do diagrama de proporcionalidade apresentadas nos
slides anteriores, obedecendo=se aos criterios de primeira obrigação e segunda
obrigação.
4) Relacionamos separadamente os investimentos de “primeira obrigação” e
“segunda obrigação”:
Prestações de Primeira obrigação são as prestações originais transferidas para a
data focal. Prestações de Segunda obrigação são as parcelas que irão “substituir”
a forma original de pagamento e que são transferidas para a data focal. A partir
daí se faz o somatório Σ 1a primeira obrigação = Σ 2a segunda obrigação
58
WWW.SUPERPROVAS.COM

59. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
Exemplo prático:
Uma pessoa deve pagar uma dívida em duas prestações, sendo a primeira no valor
de R$50.000, vencível daqui a 3 anos, e a segunda, no valor de $60.000, a pagar da
qui a 5 anos. Ela deseja trocar esse débito por dois outros iguais, pagáveis daqui a
1 ano e 2 anos, respectivamente. Qual é o valor de cada pagamento, considerando
-se a taxa de desconto comercial simples de 10% a.a. e a data focal “zero”?.
1) Fazendo o desenho representativo da questão:
Figura 1
Figura 2
WWW.SUPERPROVAS.COM
59

60. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
2) A data focal escolhida foi a data zero. O regime foi simples comercial.
3) Identificamos quais são os investimentos de primeira obrigação e segunda
obrigação que serão transferidas para a data focal (conforme desenho do slide
anterior).
4) Como a questão fala em Juros comerciais então usaremos a fórmula
A=N (1-IT) e como o investimento será transportado para a esquerda em questão
de juros comerciais devemos multiplicar o investimento por (1-IT).
Transportando as primeiras obrigações para a data focal zero (figura 1)
50.000 . (1 – 0,1 . 3) + 60.000 . (1 – 0,1.5)
Transportando as segundas obrigações pra data zero (figura 2)
 X . (1 – 0,1 . 1) + X . (1 – 0,1 . 2)
60
WWW.SUPERPROVAS.COM

61. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
5) Fazemos o somatório Σ 1a primeira obrigação = Σ 2a segunda obrigação
A equação de equivalência, considerandose desconto comercial simples, e data focal “zero” será:
X . (1 – 0,1 . 1) + X . (1 – 0,1 . 2) = 50.000 . (1 – 0,1 . 3) + 60.000 . (1 – 0,1.5)
0,9 . X + 0,8 . X = 50.000 . 0,7 + 60.000 . 0,5
1,7 . X = 65.000
X = 38.235,29
Portanto, a dívida pode ser paga em duas prestações anuais e consecutivas iguais
a $38.235,29.
Nota: na questão poderíamos ter desenhado os diagramas proporcionais de
desconto para achar os valores atuais. Porém para ganhar tempo e não ter que
ficar desenhando os diagramas de proporcionalidade consideramos ser mais
rápido usar a metodologia de “transporte” dos investimentos, que nada mais é do
que uma operação de desconto.
61
WWW.SUPERPROVAS.COM

62. EQUIVALÊNCIA DE CAPITAIS SIMPLES
EQUIVALÊNCIA DE CAPITAIS SIMPLES
Observações:
Toda questão de equivalência de capitais poderá ser resolvida por meio de
operações de desconto :
Se uma operação de desconto falar expressamente sobre taxa de juros então
estaremos diante do Desconto Racional (por dentro). Se nada dispuser e também
não falar que a taxa de operação é uma taxa de juros utilizaremos o desconto
comercial (por fora).
Data focal: é a data de referência que se for designada pela questão deve ser a
por esta adotada. Porém se nada for falado adota-se a data zero.
Se nada for dito se o regime adotado na questão é o regime simples ou composto
adote o regime simples.
Lembrar sempre que taxa e tempo devem estar nas mesmas unidades na
resolução de questões de equivalência de capitais. Caso seja necessário mudar a
unidade da taxa usaremos o conceito de taxas proporcionais nos juros simples.
62
WWW.SUPERPROVAS.COM

63. EQUIVALÊNCIA DE CAPITAIS COMPOSTA
EQUIVALÊNCIA DE CAPITAIS COMPOSTA
EQUIVALÊNCIA DE CAPITAIS COMPOSTA
63
WWW.SUPERPROVAS.COM

64. EQUIVALÊNCIA DE CAPITAS COMPOSTA
EQUIVALÊNCIA DE CAPITAS COMPOSTA
As questões de equivalência composta seguem regras parecidas em
relação à equivalência simples conforme falaremos abaixo. Porém
existem algumas recomendações adicionais:
1)Não existe equivalência composta comercial. Sempre que
soubermos que a questão é de regime composto daremos
tratamento de desconto por dentro (racional).
2)É importante nos exercícios de equivalência composta, para evitar
divisões, escolhermos a data focal à direita do fluxo de caixa. Desta
forma os valores serão transportados até esta data focal cujo valor
futuro será o valor do investimento multiplicado por (1+i)t dará o
valor futuro deste investimento.
Na equivalência simples não importa tanto esta dica, mas na
equivalência composta importa já que a solução se tornará mais
64
difícil com a divisão.
WWW.SUPERPROVAS.COM

65. EQUIVALÊNCIA DE CAPITAIS COMPOSTA
EQUIVALÊNCIA DE CAPITAIS COMPOSTA
X
Y
CAPITAL
.
X=CAPITAL / (1+I)T
TEMPO 0
T
Y = CAPITAL (1+I)T
TEMPO 1
TEMPO 2
A equivalência composta segue as regras do desconto composto
racional (por dentro) onde: N= A (1+i) t, ou seja, se quisermos
mover o investimento para a direita deve-se multiplicar por (1+i) t o
capital do investimento. Já se quisermos deslocar para a esquerda
devemos dividir o capital do investimento por (1+i) t
65
WWW.SUPERPROVAS.COM

66. EQUIVALÊNCIA DE CAPITAIS COMPOSTA
EQUIVALÊNCIA DE CAPITAIS COMPOSTA
Exemplo prático: Uma pessoa tomou um empréstimo à taxa de
4% ao mês com juros compostos capitalizados mensalmente.
Este emprésticmo deve ser pago em duas parcelas mensais e
iguais a R$1.000,00 daqui a 13 e 14 meses respectivamente. O
valor que mais se aproxima do valor de um único pagamento, no
décimo quinto mês que substitui estes dois pagamentos é:
1) Desenhando o fluxo de caixa:
x
1000
0
1000
13
14
15
(I )
(I )
(II )
66
WWW.SUPERPROVAS.COM

67. EQUIVALÊNCIA DE CAPITAIS COMPOSTA
EQUIVALÊNCIA DE CAPITAIS COMPOSTA
2) A data focal escolhido é o da localização de X . O regime é composto.
3) Identificamos quais são os investimentos de primeira obrigação e segunda
obrigação que serão transferidas para a data focal (descritos como (I) e (II) no
fluxo de caixa). A segunda obrigação abrigará o valor de X.
4) Como a questão fala em Juros racionais (em equivalência composta só teremos
questões de juros racionais – para dentro) então usaremos a fórmula A=N (1+I) t e
como o investimento será transportado para a direta (data focal de x = 15 meses)
devemos multiplicar a prestação por (1+I)t
Transportando as primeiras obrigações para a data focal de X (figura 1)
E=1000 x (1 + 0,04) 2  E=1000x1,0816 E=1.081,60 (obrigação 1)
E=1000 x(1++0,04) 1  E=1000x1,004  E-1.040,00 (obrigação 2)
Como x já está na data focal não será necessário transferir X.
5) Fazendo a somatória onde a somatória das primeiras obrigações devem ser
iguais à somatória das segundas obrigações Σ 1a primeira obrigação = Σ 2a segunda
obrigação  X = 1.081,60 + 1040,00  x = 2.121,60 (resposta).
67
WWW.SUPERPROVAS.COM

68. REGIME COMPOSTOS E OS LOGARÍTIMOS
REGIME COMPOSTOS E OS LOGARÍTIMOS
REGIME COMPOSTO e LOGARITMOS:
Eventualmente, resposta de Questão, pode vir em termos de Logaritmos.
Propriedade dos Logaritmos : se tivermos: o logaritmo de um valor qqer (X) que
esteja elevado a um expoente (Y), O valor do expoente sairá de onde está e
migrará para fora do logaritmo.
A Fórmula de Juros Compostos:
M= C*(1+i)n
Isolando o parêntese famoso: (1+i)n = M/C
Acrescentando log dos 2 lados da equação:log (1+i) n = log (M/C)
Lembrando da Propriedade dos Logaritmos: n*log (1+i) = log (M/C)
Fórmula: n*log (1+i) = log (M/C)/log (1+i)
WWW.SUPERPROVAS.COM
68

69. REGIME COMPOSTOS E OS LOGARÍTIMOS
REGIME COMPOSTOS E OS LOGARÍTIMOS
Se a questão perguntar o valor de n e se a resposta vier em termos de Logaritmos:
n= log (M/C) / log (1+i)
Exemplo prático: se os dados da questão são: M=2.000 C=1.000 i=5% qual seria o valor de
t representado em forma logarítimica?
Resposta: poderemos representar o valor de “t” na equação M= C (1+i)
logarítimos:
t
após aplicar
1) Arrumando a fórmula: M/C=(1+i) t
2) Aplicando logarítimos dos dois lados: Log (M /C)= t log (1+i)
Temos então que: => t = log(2.000/1.000) / log (1+0,05)
A resposta a ser assinalada do valor de t na questão será t= log(2) / log 1,05
Algumas bancas colocam o resultado em forma logarítima para dificultar. Deve-se então
aplicar log dos dois lados e usar as propriedades dos logarítimos para ter a resposta certa.
69
WWW.SUPERPROVAS.COM

70. RENDAS CERTAS
RENDAS CERTAS
RENDAS CERTAS
70
WWW.SUPERPROVAS.COM

71. RENDAS CERTAS
RENDAS CERTAS
O capítulo de matemática financeira que trata de rendas certas dedica-se ao
estudo do fluxo de caixa com o modelo mais simples desenhado abaixo. Como
exemplo prático podemos citar o caso de sucessivas poupanças de mesmo valor e
que possui o regaste do valor total equivalente a todo período desta poupança na
mesma data do último depósito. O regime usado será o de juros compostos.
T
T=P. S n¬ i *
P
P
P
P
* Onde T é o valor total a ser resgatado ao fim das aplicações, P é o valor da
parcela, Sn,i é o valor obtido em tabela e é chamado de fator de acumulação de
capital de uma série, n é o número de parcelas (e não o tempo), i é a taxa de
operação
71
WWW.SUPERPROVAS.COM

72. RENDAS CERTAS
RENDAS CERTAS
Apresentamos a tabela que será usada em exercícios de rendas certas (S n,i).
Lembramos que ao multiplicarmos S n,i pelos valores das prestações teremos o valor
futuro de uma série de pagamentos:
72
WWW.SUPERPROVAS.COM

73. RENDAS CERTAS
RENDAS CERTAS
Mas e se a Prova Não trouxer a Tabela de Rendas Certas?
Temos que conhecer a a Fórmula do Fator de Rendas Certas o S n¬ i
e usar sua fórmula se não for fornecida tabela na prova.
Forma Mnemônica para lembrar da Fórmula:
1º) Começamos com o parêntese mais famoso!!
S n¬ i = (1+i)n
2º) Subtraímos o parênteses famoso por 1
MACETE!!
S n¬ i = (1+i)n - 1
3º) dividimos a equação pela taxa e temos a fórmula final:
S n¬ i = (1+i)n – 1
i
73
WWW.SUPERPROVAS.COM

74. RENDAS CERTAS
RENDAS CERTAS
Mas e se modelo estiver deslocado na base de tempo. O que fazer?.
Na prática podemos achar o Valor de T e depois transportar o valor de T para a
data futura.
T1
P
T2
P
No caso se modelo estiver deslocado na base de tempo. O que fazer?.
Na prática podemos achar o Valor de T1 e depois transportar o valor de T1 para
a data futura T2 . Para isto basta multiplicar T1 por (1+i) t
74
WWW.SUPERPROVAS.COM

75. RENDAS CERTAS
RENDAS CERTAS
Exemplo prático 1: Silvério resolveu fazer aplicações durante 6 meses no Banco
Prosperidade sempre no dia 30 de cada mês de quantias iguais de 1000 reais a
uma taxa de 3% ao mês. Qual o valor resgatado 3 meses após a última aplicação?.
.
Calculamos T pela fórmula:
T=P. S n¬ i
T = 1000 x 6,46841
T=6.468,41
A partir de então resolvemos
transportando o valor obtido T
para o último período pela
multiplicação
de
T
por
(1+i)t..Obteremos o valor de X
que será M=7.068,20.
75
WWW.SUPERPROVAS.COM

76. RENDAS CERTAS
RENDAS CERTAS
Exemplo prático 2: um outro tipo de exercício ocorre com a justaposição de vários
fluxos constantes de diferentes valores (é como se fosse uma poupança em que
aumentamos o valor do depósito após transcorrido determinado período de
tempo. Neste exercício calculamos por nível e depois somamos:
.
1º) Nível
2º) Nível
P=1.000
n=12m
i=2%a.m.
=> T = 13.412,09
P=1.000
P=1.000
n=8m
n=4m
i=2%a.m.
i=2%a.m.
=> T’ = 8.582,969 => T’’ = 4.121,608
T=P. S n¬ i
T=P. S n¬ i
3º) Nível
T=P. S n¬ i
X= T + T’ + T’’
X=26.116,38
76
WWW.SUPERPROVAS.COM

77. AMORTIZAÇÃO
AMORTIZAÇÃO
AMORTIZAÇÃO
77
WWW.SUPERPROVAS.COM

78. AMORTIZAÇÃO
AMORTIZAÇÃO
O modelo básico de amortização é o apresentado abaixo. Trata-se de uma operação de
compra à prazo sem entrada.
Na amortização as parcelas são usadas para liquidar um valor anterior.
A diferença de rendas certas com relação à amortização é que em rendas certas usamos
as parcelas para acumular, somente isto. Iremos usar a fórmula do fator de valor atual de
uma série de pagamentos A n¬ i durante o estudo das amortização.
Notem que o A n¬ i nos dá os valores atuais de uma série de pagamentos (valor atual) e
o S n¬ nos dá o valor futuro de uma série de pagamentos. Ambos podem ser
encontrados na sua tabela respectiva.
T
T=P. A n¬ i
78
WWW.SUPERPROVAS.COM

79. AMORTIZAÇÃO
AMORTIZAÇÃO
A fórmula usada em amortizações é:
T=P. A n¬ i
Onde:
T= valor a ser amortizado
P= prestação
A n, i = fator de valor atual de uma série de pagamentos, sendo n= número de
prestações e i a taxa de juros utiizada na mesma unidade de tempo da questão.
Lei da amortização: para efeito de utilização da fórmula de amortização a
primeira parcela deverá estar sempre ao final do primeiro período.
Nota: lembrem-se que as parcelas (prestações) devem ser sempre do mesmo
valor. Além disto os intervalos de tempo devem ser sempre iguais. O regime
adotado sempre será o composto (taxa de juros composta).
79
WWW.SUPERPROVAS.COM

80. AMORTIZAÇÃO
AMORTIZAÇÃO
TABELA DE FATOR DE VALOR ATUAL DE UMA SÉRIE DE PAGAMENTOS:
Lembramos que em amortizações trabalharemos com a tabela de An,i abaixo:
80
WWW.SUPERPROVAS.COM

81. AMORTIZAÇÃO
AMORTIZAÇÃO
Mas e se a banca não disponibilizar tabela?
Daí teremos que conhecer a fórmula abaixo:
(1 + i ) n − 1
a n ,i =
n
i (1 + i )
Começo pelo parênteseses famoso
subtraio de 1 e divido por i ou também
divido pelo parenteses famoso
Colocaremos lado a lado as fórmulas do fator de acumulação de uma série de pagamentos
e a fórmula de aacumulação de uma série de pagamentos para facilitar a memorização:
(1 + i ) − 1
a n ,i =
n
i (1 + i )
n
S n¬ i = (1+i)n – 1
i
Ou seja: o que muda é o valor do denominador onde
A n,i . (1+i) n = S n,i
81
WWW.SUPERPROVAS.COM

82. AMORTIZAÇÃO
AMORTIZAÇÃO
Exemplo prático de questão de amortização:
Josimar comprou um conjunto de sofás no valor de R$5000,00 em negócío sem entrada. Se ele
pretende parcelar pagando prestações iguais durante meses, qual será o valor das prestações
se a taxa de juros é igual a i=3%a.m.
Qual o valor da Parcela?
T=5.000 / n=6 parcelas / i=3%a.m. P=?, T= A n¬ i
1) Cálculo do valor das prestações::
T= A n¬ i  5.000=P * A 6¬ 3,
Após verificar na tabela de amortização temos que:=> 5.000=P * 5,417191 =>
P=5.000/5,417191 => P = 922.98 (valor de cada prestação = resposta).
2) Cálculo para saber o valor. dos JUROS pagos:
Juros = Soma das parcelas - T
Soma das Parcelas = 6*922,98
Juros = 5.533,68-5.000 = 533,68
Juros =533,68
82
WWW.SUPERPROVAS.COM

83. AMORTIZAÇÃO
AMORTIZAÇÃO
MODALIDADES DE AMORTIZAÇÃO
SAC/PRICE/AMERICANO
83
WWW.SUPERPROVAS.COM

84. SISTEMAS DE AMORTIZAÇÃO - SAC
SISTEMAS DE AMORTIZAÇÃO - SAC
Sistema de amortização constante (SAC):
As parcelas de amortização são iguais entre si. Os juros são calculados a cada período,
multiplicando-se a taxa de juros contratada na forma unitária pelo saldo devedor existente
no período anterior. Neste sistema as prestações são continuamente decrescentes.
Prestação
juros
amortização
Período
Como o saldo devedor decresce a cada período, os juros calculados em cima deste saldo
Devedor vai descrescendo também. Neste sistema paga-se os juros do principal +
um valor fixo de amortização.
84
WWW.SUPERPROVAS.COM

85. SISTEMAS DE AMORTIZAÇÃO - SAC
SISTEMAS DE AMORTIZAÇÃO - SAC
Exemplo prático: Uma empresa que emprestado R$ 100.000 que o banco entrega no ato.
Sabendo que o banco concedeu 3anos de carência e que os juros serão pagos anualmente e
ainda, que taxa de juros é de 10% ao ano e que o principal será amortizado em 4 parcelas
anuais, construir a planilha.
Resolução: a amortização anual é: 100.000/4 = 25000
Vamos admitir que o principal fora emprestado no ínício do primeiro ano e que as
prestações e os juros sejam pagos no fim de cada ano.
85
WWW.SUPERPROVAS.COM

86. SISTEMAS DE AMORTIZAÇÃO - SAC
SISTEMAS DE AMORTIZAÇÃO - SAC
O racicínio foi o seguinte:
a)Do início do primeiro ano (data zero) até o fim do terceiro ano, temos 3 períodos, que
correspondem à carência.Logo após terminado o período de carência, temos a primeira
amortização de R$ 25000.
b) Os juros são calculados sempre sobre o saldo devedor do período anterior, ou seja:
sendo Jk o juro devido no período k, sendo i a taxa de juros e Sdk-1 o saldo devedor do
período temos que: Jk= i SDk-1.
Observe, no exemplo, que o juro do período é calculado multiplicando-se a taxa (na forma
unitária pelo saldo devedor do período anterior.
c) A prestação é obtida somando-se ao final de cada período a amortização com os juros.
d) A linha de total serve para verificar se as somas batem e, portanto, se as contas estão
certas.
86
WWW.SUPERPROVAS.COM

87. SISTEMAS DE AMORTIZAÇÃO - PRICE
SISTEMAS DE AMORTIZAÇÃO - PRICE
Sistema de Francês (price)
As prestações são iguais entre si e calculadas de tal modo que uma parte paga os juros e
outra parte “paga” o principal (amortiza). A dívida fica completamente saldada na última
prestação.
Prestação
Prestação
Juros
Período
Por este sistema., o mutuário obriga-se a devolver o principal mais os juros em prestações
iguais entre si e periódicas. Temos que resolver, portanto dois problemas para construir a
planilha: como calcular a prestação e como separar a amortização dos juros
87
WWW.SUPERPROVAS.COM

88. SISTEMAS DE AMORTIZAÇÃO - PRICE
SISTEMAS DE AMORTIZAÇÃO - PRICE
Exemplo prático: um banco empresta R$ 100.000, entregues no ato, sem prazo de carência.
Sabendo-se que o banco utiliza o sistema francês, que a taxa contratada foi de 10% e que o
banco quer a devolução em 5 prestações .Construa a planilha respectiva:
Resolução: se o principal vai ser devolvido em 5 prestações igual e postecipadas, temos
exatamente uma anuidade que se transforma em nosso modelo básico.
R=100.000/ an¬ i
P=R. an¬ i
R=100.000/3,790787
R= 26.378,75
Teremos então 5 prestações iguals de R$ 28.379,75. Os juros serão calculados
aplicando-se a taxa de juros sobre o saldo devedor do período anterior.
A amortização será calculada pela diferença entre a prestação e o juro do período. Por
sua vez, o saldo devedor do período será calculado como sendo a diferença entre o
saldo devedor do período anterior e a amortização do período
88
WWW.SUPERPROVAS.COM

89. SISTEMAS DE AMORTIZAÇÃO - PRICE
SISTEMAS DE AMORTIZAÇÃO - PRICE
Exemplo prático
O procedimento, portanto, é o seguinte:
a)Calcula-se a prestação R
b)Calculam-se para cada período (k) os juros sobe o saldo devedor (JK= i. Sd k-1)
c)Faz=se para cada período (k) a diferença entre a prestação e os juros obtendo-se o vaor
da amortização (Ak= R-Jk)
d)A diferença em cada período (k) entre o saldo devedor do período anterior e a
amortização do período dá o devedor do período. Sdk= Sdk-1 - Ak
89
WWW.SUPERPROVAS.COM

90. SISTEMAS DE AMORTIZAÇÃO – AMERICANO
SISTEMAS DE AMORTIZAÇÃO – AMERICANO
Sistema americano
Após um certo prazo o devedor paga em uma única parcela o capital emprestado. A
modalidade mais comum é aquela em que o devedor paga juros durante a carência.
Prestação
PRINCIPAL
Juros
Período
O devedor deve querer aplicar recursos disponíveis e gerar um fundo que igale o
desembolso a ser efetuado para amortizar oprincipal. Tal fundo é conhecido para sinkin
fund na literatura americana e , na brasileira, por fundo de amortização.
90
WWW.SUPERPROVAS.COM

91. ANÁLISE DE INVESTIMENTOS
ANÁLISE DE INVESTIMENTOS
ANÁLISE DE INVESTIMENTOS
91
WWW.SUPERPROVAS.COM

92. ANÁLISE DE INVESTIMENTOS
ANÁLISE DE INVESTIMENTOS
Fazer um estudo de análise de investimento é como trabalhar com um sistema de
amortização Francês. A grande diferença é que, nesse caso, as prestações não são
constantes.
Taxa Interna de Retorno (TIR): Define-se como a taxa de desconto em que o Valor
Presente do fluxo de caixa futuro de um investimento se iguala ao custo do investimento. É
calculada mediante um processo de tentativa e erro.Quando os valores presentes líquidos
do custo e dos retornos se igualam a zero, a taxa dedesconto utilizada é a TIR.
Se essa taxa excede o retorno exigido - chamada taxa de atratividade - o investimento é
aceitável. Pode haver mais de uma TIR para determinado conjunto de fluxos de caixa.
A Taxa Mínima de Atratividade (TMA): é uma taxa de juros que representa o mínimo que
um investidor se propõe a ganhar quando faz um investimento, ou o máximo que um
tomador de dinheiro se propõe a pagar quando faz um financiamento.
O valor presente líquido (VPL): Também conhecido como valor atual líquido (VAL) ou
método do valor atual, é a fórmula matemático-financeira de se determinar o valor
presente de pagamentos futuros descontados a uma taxa de juros apropriada, menos o
custo do investimento inicial.
92
WWW.SUPERPROVAS.COM

93. MATEMÁTICA FINANCEIRA
MATEMÁTICA FINANCEIRA
Exemplo típico de questão envolvendo análise de investimentos :
(Universidade Federal da Fronteira Sul – Economista – 2009 – FEPESE)
Os métodos de análise de investimentos do valor presente líquido e da taxa
interna de retorno estão de certa forma relacionados. Considerando um
determinado valor presente líquido (VPL), uma taxa interna de retorno (TIR), e
um custo de oportunidade i%, o critério aceitar-rejeitar dos métodos de
avaliação de investimentos deve estar de acordo com a seguinte alternativa:
a) Se VPL > 0, a TIR < i%.
b) Se VPL > 0, a TIR = i%.
c) Se VPL = 0, a TIR > i%.
d) Se VPL > 0, a TIR > i%.
e) Se VPL < 0, a TIR = i%.
Resolução
Para que o projeto seja viável o VPL deve ser positivo e taxa interna de retorno
deve ser maior do que a taxa mínima de atratividade.
Gabarito : letra D
WWW.SUPERPROVAS.COM
93

94. MATEMÁTICA FINANCEIRA
MATEMÁTICA FINANCEIRA
BONUS E CUPONS
94
WWW.SUPERPROVAS.COM

95. BONUS E CUPONS
BONUS E CUPONS
Uma nova abordagem de questões de matemática financeira no que se refere a
empréstimos são as questões que envolvem bônus e cupons. Trata-se de um empréstimo
feito por um país no mercado internacional, para obter este empréstimo o país emite títulos
chamados de bônus. Os cupons são as prestações e o valor do título/bônus é chamado de
preço de lançamento. Caso a compra do título for feita por um valor abaixo do preço de
lançamento teremos deságio, caso contrário teremos ágio.
O país que propõe o título irá devolver o empréstimo em forma de cupons + na data em que
pagar a última prestação deverá devolver também o valor nominal do título.
Quando surgir uma questão com esta nova “linguagem” entendamos que se trata de uma
questão de empréstimo + devolução.
95
WWW.SUPERPROVAS.COM

96. BONUS E CUPONS
BONUS E CUPONS
Definições:
Valor de lançamento do bônus (X) é o valor de venda do bônus no mercado internacional,
ou seja, é o recurso captado (o valor que o país pega emprestado) no mercado
internacional. O bônus é um título de crédito, e o comprador deste bônus terá direito de
receber pagamentos futuros referentes à sua compra.
Quando o valor do bônus é maior que o seu valor nominal dizemos que ocorre um ágio e
quando menor, ocorre um deságio.
Valor nominal do bônus (N) – é o valor deface do bônus. Ou seja, é o valor escrito em papel
, indicando quanto vale o título.
Cupons (P) – parcelas periódicas pagas ao comprador do bônus. Já são parte da devolução
que o país está realizando.
Taxa de Juros da operação (i) – taxa de empréstimo (do ponto de vista do país que captou
os recursos), ou taxa de aplicação (do ponto de vista de quem emprestou os recursos). Será
uma taxa de juros composta.
96
WWW.SUPERPROVAS.COM

97. MATEMÁTICA FINANCEIRA
MATEMÁTICA FINANCEIRA
Fórmula para resolução:
(Valor do Bônus) + (Cupom) x S(n;i) = (Valor do Bônus) x (1+i) n x (ÁGIO/DESÁGIO)
Exemplo prático: Um bônus possui valor nominal de US$ 1,000.00 e contém quatro
cupons semestrais de US$ 50.00 cada, sendo que o primeiro cupom vence ao fim de
seis meses, e assim sucessivamente, até que, junto com o quarto cupom, o comprador
do bônus recebe o valor nominal do bônus de volta, obtendo assim uma remuneração
nominal de 5% ao semestre em sua aplicação de capital. Abstraindo custos
administrativos e comissões, calcule o deságio necessário sobre o valor nominal do
bônus para que a aplicação de compra do bônus produza um ganho real de 6% ao
semestre.
a) 3%
b) 3,196%
c) 3,465%
d) 5%
e) 6,21%
(Valor do Bônus) + (Cupom) x S(n;i) = (Valor do Bônus) x (1+i) n x (ÁGIO/DESÁGIO)
1000 + 50 x S(4;6%) = 1000 x (1,06)4 x Deságio
Deságio = 1.218,73 / 1.262,47 = 0,9653  Deságio de 3,464%
Na segunda parte da fórmula deves-se usar a taxa EFETIVA, e nao a NOMINAL
97
WWW.SUPERPROVAS.COM

98. MATEMÁTICA FINANCEIRA
MATEMÁTICA FINANCEIRA
BIZUS
98
WWW.SUPERPROVAS.COM

99. BIZUS
BIZUS
Em uma operação de juros, se o enunciado da questão não especificar (de
forma explícita ou implícita) o regime a ser adotado (se simples ou composto),
adotar o regime de juros simples.
Em uma operação de juros simples, se nada vier especificado quanto à
modalidade, adotaremos os juros simples comerciais, ou seja, aquele que
considera todos os meses do ano como tendo 30 dias.
Juros Simples Comerciais = Juros Simples Ordinários
Juros Simples Comerciais ≠ Juros Simples Exatos.
Juros Simples Exatos: aquele que considera o calendário comum! Ou seja, o ano
com 365 dias! (366, se bissexto!).
Em uma operação de juros, se o enunciado da questão não especificar (de forma
explícita ou implícita) o regime a ser adotado (se simples ou composto), adotar o
regime de juros simples.
Em uma operação de juros simples, se nada vier especificado quanto à
modalidade, adotaremos os juros simples comerciais, ou seja, aquele que
considera todos os meses do ano como tendo 30 dias.
99
WWW.SUPERPROVAS.COM

100. BIZUS
BIZUS
Resolveremos questões de Juros Simples, utilizando apenas uma pequena
proporção, que será formulada com os dados do enunciado, e tendo por base
um esquema ilustrativo do Cálculo dos Juros Simples.
A taxa (i) e o tempo (n) devem estar na mesma unidade (dia ou mês ou ano
ou etc.).
No regime de Juros Simples utilizaremos sempre as taxas na forma percentual
(sem a %).
No regime de Juros Compostos utilizaremos sempre as taxas na forma
unitária)
Em uma questão de juros simples, sempre que for preciso alterar a unidade de
tempo da taxa, utilizaremos o conceito de taxas proporcionais!
Se o enunciado de uma questão de juros não especificar o regime a ser
adotado (simples ou composto), mas trouxer um dos seguintes termos no seu
enunciado: capitalização, capitalizado, taxa nominal, inflação, capital
acumulado, juros cumulativos, juros sobre juros, então adotaremos o regime
de juros compostos!
100
WWW.SUPERPROVAS.COM

101. BIZUS
BIZUS
Observe a seguinte taxa: 10% ao mês, com capitalização mensal. Esta não é
uma taxa nominal (uma vez que o tempo da taxa é o mesmo tempo da
capitalização). Contudo, o simples fato de haver a palavra “capitalização”, já nos
indicará que o regime a ser adotado será o regime composto
Em uma questão de juros compostos, sempre que a taxa da operação for
apresentada como uma taxa nominal, imediatamente a converteremos em uma
taxa efetiva.
Esta conversão de taxa nominal em taxa efetiva é realizada como se
estivéssemos no regime de juros simples!! Ou seja, “faremos de conta” que são
taxas proporcionais!
Para se aplicar a fórmula dos juros compostos, deveremos ter uma única
preocupação: que taxa e tempo estejam na mesma unidade!
Se nos dados da questão, taxa e tempo estiverem em unidades diferentes,
tentaremos mexer com o tempo e deixá-lo compatível com a taxa.
Em uma questão de juros compostos, sempre que for preciso alterar a
unidade de tempo da taxa (efetiva), utilizaremos o conceito de Taxas
equivalentes {1+I = (1+i)n}
101
WWW.SUPERPROVAS.COM

102. BIZUS
BIZUS
Desconto Bancário = Desconto Comercial acrescido de taxas administrativas!.
Questões de Equivalência de Capitais se transformarão em pequenas
questões de Desconto! Cabe observarmos se o regime de desconto a ser
adotado nestas questões será o simples ou o composto! Além disso, devemos
observar a modalidade do desconto: se por dentro ou por fora!.
Se a questão é de equivalência composta de capitais então para resolvermos
a mesma usaremos sempre operações de desconto composto racional, ou
igualmente operações de capitalização de juros compostos!.
Questões de Rendas Certas e Amortizações acontecem, para efeito de
utilização das fórmulas estudadas, sempre no regime composto!.
Para aplicação dos dados da questão nas fórmulas de rendas certas e
amortização, a unidade da taxa empregada na operação deve ser a mesma
unidade do intervalo entre as aplicações das parcelas.

Ex.: Se as parcelas são mensais, então a taxa deve estar ao mês!
Se as parcelas são semestrais, então a taxa deve estar ao semestre!
102
WWW.SUPERPROVAS.COM

103. BIZUS
BIZUS
Se esta compatibilidade não ocorrer nos dados da questão, devemos alterar a
unidade da taxa, deixando-a igual à periodicidade das aplicações, utilizando-nos
do conceito de taxas equivalentes, uma vez que estamos trabalhando no regime
composto!
Em questões de Cálculo do Montante em Rendas Certas, deveremos nos
lembrar que a data do resgate coincidirá, para efeito de utilização da fórmula,
com a data da última aplicação!
Em questões de Cálculo do Valor Atual em Rendas Certas e Sistema Francês
de Amortização, devemos nos lembrar que a primeira parcela (prestação), para
efeitos de utilização da fórmula, ocorrerá ao final do primeiro período após a
data do valor T (a ser amortizado)!
Palavras-chave que definem o regime composto: capitalização, inflação,
calcule a taxa equivalente
103
WWW.SUPERPROVAS.COM

104. BIZUS
BIZUS
Calcule os juros em relação ao capital inicial = calcule a taxa equivalente No
juros comercial ou ordinário todos os meses têm 30 dias: id=ia/360
Atente: 365=5x73
Taxas médias, Prazo médio e Capital médio:
Numerador sempre igual e denominador: some aquilo que está sendo
pedido. Simplifique logo na coluna (o que aparece cima e embaixo).
Lembrem-se que em uma prova poderá ou não ser fornecida tabelas. A Esaf
costuma fornecer as tabelas de valor atual e valor de acumulação tanto para
séries quanto para um único investimento. São estas três tabelas que
facilitam os cálculos. Porém algumas bancas não fornecem as fórmulas então
neste caso deve-se saber as fórmulas na hora da prova.
Além disto é importante saber que cada tabela está atrelada a um tipo de
fluxo que poderá ser postecipado, antecipado, etc.
104
WWW.SUPERPROVAS.COM

105. MATEMÁTICA FINANCEIRA
MATEMÁTICA FINANCEIRA
FIM DO RESUMO
WWW.SUPERPROVAS.COM
105
WWW.SUPERPROVAS.COM