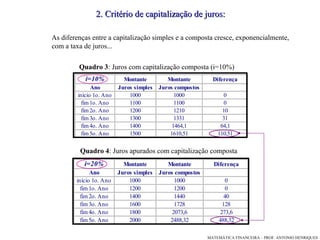
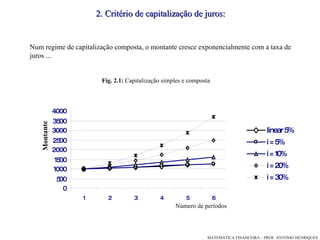
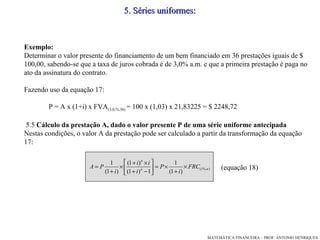
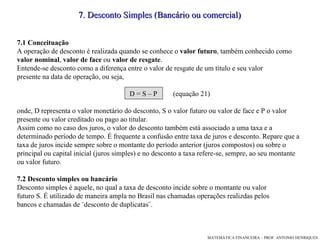
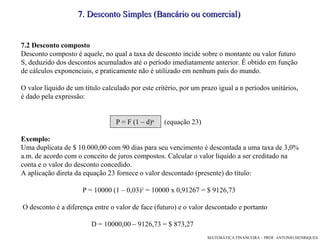
O documento discute os critérios de capitalização de juros simples e compostos. Apresenta as fórmulas para calcular juros, montantes e valores atuais/futuros em cada regime, ilustrando com exemplos numéricos. Explica a diferença entre as progressões aritmética e geométrica que modelam cada método.

1. FACULDADE DE ENGENHARIA DE GUARATINGUETÁ ECONOMIA DE EMPRESAS TÓPICOS DE ENGENHARIA ECONÔMICA PROF. Dr. ANTONIO HENRIQUES DE ARAÚJO JR

2. EMENTA: O valor do dinheiro no tempo. Critérios de capitalização de juros. Juros simples Juros compostos. Conversões de taxas de juros. Fluxo de caixa. Series simples e uniformes. Series equivalentes. Avaliação de investimento. Descontos em operações comerciais. Efeito de taxas e impostos em operações financeiras. O uso das funções financeiras no Excel.

3. BIBLIOGRAFIA: BIBLIOGRAFIA BASICA: MATEMATICA FINANCEIRA E SUAS APLICAÇÕES BASICAS, Assaf, Alexandre Neto, Editora Atlas, 4 a . Edição, 419 p., São Paulo, 1996. MATEMATICA FINA N CEIRA Vieira, Jose Dutra Sobrinho, Editora Atlas, 7a. Edição, 409 p., São Paulo, 2000. MATEMATICA FINANCEIRA Puccini, 5a.Edição, 318p. São Paulo 1998. BIBLIOGRAFIA COMPLEMENTAR: MATEMATICA FINANCEIRA USANDO EXCEL 5 e 7, Laponi, J. Carlos, Ed. Laponi Treinameto, São Paulo, 1996. ENGINEERING ECONOMY. Sullivan, W.G; Wicks, E. M., 12 th edition, Prentice Hall, N.Jersey, 2003.

4. Procedimentos Metodológicos: Os alunos aprenderão , inicialmente, a racio ci nar e resolver problemas de matemática financeira com o conceito de fluxo de caixa e a utilização de formulas. Com o domínio desta ferramenta, aprenderão a utilizar outros métodos, como resolução destes mesmos problemas com o uso de tabelas financeiras especificas, e aprenderão a construir , com o uso do Excel , tabelas de desconto e a resolver problemas m ais complexos. A teoria sera fartamente ilustrada com exercícios a serem resolvidos em sala de aula e em casa. Recursos Didáticos: Retro-projetor, calculadora 12-C, e micro-computador (laboratório,1 aula).

5. Avaliação PROVA P3 e P4 ; Exercício s ; Participação em sala.

6. 1. Introdução: O valor do dinheiro no tempo 1.1 O valor do dinheiro no tempo A matemática financeira trata do estudo do valor do dinheiro ao longo do tempo. O seu objetivo básico é o de efetuar análises e comparações dos vários fluxos de entrada e saída de caixa , verificados em diferentes momentos. Sabemos , i ntuitivamente , que é melhor termos uma determinada quantia ou crédito hoje do que em, digamos, 3 anos. Receber uma quantia hoje ou no futuro não é a mesma coisa. 1.2 Definição de juros e de taxa de juros Para Dutra (2000) juro representa a remuneração do capital emprestado, podendo ser ntendido como o aluguel pago pelo uso do dinheiro. Pode ser definido, ainda, c omo o custo pelo uso do dinheiro. Taxa de juro é a relação entre o juro recebido ou pago ao final de certo período de tempo de tempo (prazo) e o capital inicialmente aplicado , sendo definido como segue. I = J/C (equação 1)‏ Onde I é a taxa de juro, J o valor do juro pago e C o capital inicial. Observe que a taxa de juro deve ser, sempre, expressa numa unidade de tempo , p .e. 20% a.a., 15% a.t., etc.

7. 1. Introdução: Formação da taxa de juros 1.3 Fatores que influenciam, do ponto de vista microeconomico, as taxas de juros Alguns fatores influenciam a formação da taxa de juros: Custo de captação (taxa paga aos investidores + rateio de despesas administrativas); Margem de lucro, taxa para remunerar o capital investido; Taxa de risco (inadiplencia) que é calculada pela relação entre volume de empréstimos não honrados e volume total de empréstimos concedidos; Inflação, taxa embutida para compensar a perda de poder aquisitivo da Moeda; Impostos.

8. 2.1 Critérios de capitalização Os critérios ou regimes de capitalização demonstram como os juros são formados e incorporados sucessivamente ao capital ao longo do tempo. Podem ser identificados dois regimes de capitalização de juros: simples (linear) e composto (exponencial). 2.2 Regime de capitalização simples O regime de capitalização simples comporta-se como uma progressão aritmética (PA) , com os juros crescendo linearmente ao longo do tempo. Por este critério , os juros só incidem sobre o capital inicial (principal). Admita-se um depósito de R$1.000 remunerados a uma taxa de 10% a.a. Os juros apurados ao longo de 5 anos, os juros acumulados e os montantes (capital inicial +juros) estão demonstrados no quadro 1 : 2. Critério de capitalização de juros: Quadro 1 : Juros apurados com capitalização simples

9. 2.3 Regime de capitalização composta No regime de capitalização composta são incorporados ao capital , não apenas os juros referentes a cada período , mas também os juros incidentes sobre os juros acumulados até o período anterior. Neste regime de capitalização, o valor dos juros cresce, exponencialmente, em função do tempo. O conceito de montante aqui, é o mesmo da capitalização simples, ou seja é a soma do capital aplicado ou devido mais o valor dos juros correspondentes ao prazo de aplicação ou da dívida. O comportamento equivale ao de um a progressão geométrica (PG) , incidindo os juros sempre sobre o saldo apurado no inicio do período imediatamente anterior. Considere-se os mesmo R$ 1000,00 de capital inicial e a mesma taxa de juros de 10% a.a. a dotados no exemplo anterior. O cálculo dos juros acumulados e do montante são ilustrad os no quadro 2: Quadro 2: Juros apurados com capitalização composta 2. Critério de capitalização de juros:

10. 2. Critério de capitalização de juros: As diferenças entre a capitalização simples e a composta cresce, e xponencialmente, com a taxa de juros... Quadro 4 : Juros apurados com capitalização composta Quadro 3 : Juros com capitalização composta (i=10%)‏

11. 2. Critério de capitalização de juros: Num regime de capitalização composta, o montante cresce exponencialmente com a taxa de juros ... Número de períodos Montante Fig. 2.1: Capitalização simples e composta

12. 2. Critério de capitalização de juros: 2.4 Capitalização simples 2.4.1 Cálculos dos juros O valor dos juros num regime de capitalização simples é dado pela expressão: onde: J = valor do Juro em valores monetários, P = valor do capital inicial ou principal, e n = prazo ou número de períodos. Exemplo : 1. Qual é o valor dos juros correspondentes a um empréstimo de R$ 1.000,00 pelo prazo de 4 meses, sabendo-se que a taxa cobrada é de 5,0% a.a. Solução: J = P x i x n, substituindo os valores númericos, teremos, J = $ 1.000 x 0,05 x 4 = $ 200,00. (equação 2)‏

13. 2.4.2 Montante e valor atual O montante ou valor futuro, indicado por M, representa a soma do principal e dos juros referentes ao período de aplicação: M = P + J (equação 3)‏ Inserindo a equação 2 na equação 3, teremos: M = P + P x i x n ou M = P (1 + i x n ) (equação 3a)‏ Exemplo : Sabendo-se que os juros de $ 6.000,00 foram obtidos com a aplicação de $ 7.500,00 a taxa de 8% ao trimestre, pede-se calcular o prazo de aplicação. P = 7500,00 J = 6.000,00 i = 8% a.t. n = a ser calculado Solução: J = P x i x n , portanto, n = J/(P x i ) = 6000/(7500)x 0,08) = 10 trimestres. 2. Critério de capitalização de juros :

14. 1. Determinar quanto renderá um capital de $ 60.000,00 aplicado a taxa de 24% ao ano, durante 7 meses. R: $ 8.400,00. Um capital de $ 28.000,00, aplicado durante 8 meses, rendeu juros de $ 11.200. Determinar a taxa unual. R: 60 %. Durante 155 dias certo capital gerou um montante de $ 64.200. Sabendo-se que a taxa de juros é de 4 % ao mes, deteminar o valor do capital aplicado. R: $ 53.204,42. Exercícios para a segunda aula

15. 4. Qual o valor dos juros contidos no montante de $ 100.000,00, resultante da aplicação de certo capital a taxa de 42% ao ano, durante 13 meses. R: $ 31.271,48 Qual o valor a ser pago, no fim de 5 meses e 18 dias, correspondente a um empréstimo de $ 125.000,00, sabendo-se que a taxa de juros é de 27% ao semestre. R: $ 156.500,00

16. 2. Critério de capitalização de juros: 2.5 Capitalização composta 2.5.1 Cálculos dos juros num regime de capitalização composta Consideremos, num regime de capitalização composta, um principal P, ou valor presente , uma taxa de juros, i , e um montante F , também chamado de valor futuro, a ser capitalizado e um prazo n. No fim do 1 o . período , o montante S será igual a: F = P + P x i ou P (1 + i)‏ O juro pago no fim do 2o. período será igual a: P (1 + i) i Portanto, o montante S, no fim do 2o. período, será dado por: P (1 + i) + P (1 + i) I ou, F = P (1 + i) 2 . E, assim, ao término do n-ésimo período o montante F , será dado por: F = P (1 + i) n (equação 4)‏

17. O fator (1 + i) n é denominado Fator de Capitalização (FCC), sendo tabelado para uma determinada taxa i , e para um determinado número de períodos n . Adotemos no nosso curso, a seguinte notação para este fator, para uma taxa de 5% a.p. e 10 períodos, o fator FCC (5%, 10) será de (1 + 0,05) 10 ou 1,62889. Exercício : verificar, num dos textos sugerido na bibliografia, os FCCs para: i =10% a.a. e 8 anos; e i = 8% a.s. e 2 semestres 2.5.1 Cálculo do valor futuro F, dados, P, i e n Assim, dada a equação (4) podemos resolver problemas do seguinte tipo: (...) conhecido o valor do principal P , ou valor presente, a taxa de juros i e o número de períodos n a ser capitalizado, podemos calcular o Montante F, ou valor futuro , como mostrado no fluxo de caixa abaixo: 2. Critério de capitalização de juros: F = P 1 3 2 n Fig. 2.2: Fluxo de caixa da situação: Dados P, i e n calcular S.

18. Exemplo: Quanto renderá em 6 meses, um capital de $ 2000,00, aplicado a uma taxa de juros de 5% a.m. Aplicando a equação (4): S = 2000 (1 + 0,05) 6 = 2000 x 1,3400 => $ 2.680,00 2.5.2 Cálculo do valor presente P, conhecido o valor futuro F A partir da equação (4) podemos deduzir que: (equação 5)‏ O fator é denominado Fator de Atualização de Capital (FAC) e é igualmente tabelado para uma determinada taxa de juro s i e um determinado número de períodos n . Passemos a adotar a seguinte notação para este fator: dada uma taxa de juros de 4% a.p.e 5 períodos o fator FAC (4%, 5) será de 0,82193. Note que os fatores FCC e FAC são números inversos, isto é, se multiplicarmos FAC (4%, 5) por FCC (4%, 5) obteremos 1 ou, no nosso exemplo, 0,8121 x 1,21665 = 1. Exercício : verificar, num dos textos sugerido na bibliografia, os FACs para: i = 10% a.a. e 8 anos; e i = 8% a.s. e 2 semestres 2. Critério de capitalização de juros:

19. Assim, dada a equação (5) podemos resolver problemas do seguinte tipo: (...) conhecido o valor F , ou valor futuro, a taxa de juros i e o número de períodos de capitalização n, podemos calcular o valor P, ou valor presente , como mostrado no fluxo de caixa abaixo: Exemplo: Quanto deverei aplicar hoje, num regime de capitalização composta, para obter, a uma taxa de 2% a.m., em 18 meses, a quantia de $ 5.000,00. Solução: aplicando a fórmula (5), P = 5.000/(1+0,02) 18 = 5.000/1,42825 = $ 3500,78, ou, resolvendo de uma outra forma P = S FAC (2%, 18) = 5.000 x 0,70016 = $ 3.500,78. 2. Critério de capitalização de juros: F P = 1 3 2 n Fig. 2.3: Fluxo de caixa da situação: Dados S, i e n calcular P.

20. 1 . Qual o montante acumulado em 6 trimestres a uma taxa de 2% a.m. em um regime de juros compostos, a partir de um principal de $ 1.000.000,00. R: $ 1.428.250,00 Qual é o principal que deve ser investido nesta data para se obter um montante de $ 500.000,00, daqui a 2 anos, a uma taxa de 15% a.s. em um regime de juros compostos. R: $ 285.877,64 Um cidadão investiu $ 10.000 nesta data, para receber $ 14.257,60 daqui a um ano. Qual a taxa de rentabilidade mensal de seu investimento, em um regime de juros compostos. R: $ 3,0% a.m. 2. Critério de capitalização de juros:

21. 4. Quanto se terá daqui a 26 trimestres ao se aplicar $ 100.000,00 nesta data, a uma taxa de 2,75% a.m. no regime de juros compostos. R: $ 829.817,86 5. Uma pessoa deseja fazer uma aplicação financeira, de 2% a.m., de forma que possa retirar $ 10.000,00 no final do 6o.mes e $ 20.000,00 no final do décimo segundo mes. Qual o menor valor da aplicação que permite a retirada desses valores nos meses indicados. R: $ 24.650,00 Em quanto tempo triplica um capital que cresce a uma taxa de 3,0% a.m. R: 37,1 meses Que taxa de juros está embutida numa operação que dobra o capital inicial de $ 1400,00 num prazo de 14 meses. R: 5,076% a.m.

22. 3 . Conversões de taxas de juros: 3.1 Equivalencia de taxas de juros com capitalização composta Uma condição para a equivalencia de taxas de juros é que estas taxas, aplicadas sobre um mesmo principal, ou capital inicial, produzam o mesmo montante, ao final de um certo prazo n. Se uma certa taxa mensal i m é equivalente a uma certa taxa anual i a , então: P (1 + i m ) 12 = P (1 + i a ) (equação 6)‏ Dividindo a equação (6) por P: (1 + i m ) 12 = (1 + i a ) (equação 7)‏ Transformando a equação 7: ou: (equação 8)‏ Exemplo: Calcular a taxa de juro mensal, equivalente a uma taxa de 20% a.a. Aplicando a equação (8) obtemos: ; = 1,01531 – 1 => 1,531% a.m.

23. 3.2 Fórmulas para conversão de taxas de juros equivalentes Existem duas situações básicas para a conversão de taxas de juros: Conversão de uma taxa de período de tempo menor para uma taxa de período de tempo maior : Taxa semestral em taxa anual, taxa mensal em taxa anual, etc. Neste caso vamos aplicar a seguinte fórmula: i e = (1 + i q ) n - 1 (equação 9)‏ onde: i e = taxa equivalente; i q = taxa conhecida a ser convertida; n = número de períodos contidos no período da taxa de juros menor. Exemplo: converter uma taxa de 4% a.t. em taxa anual. I e = (1 + 0,04) 4 = 1,16985 => i e = 16,98% a.a. Neste caso n = 4, uma vez que um ano contém 4 trimestres. Conversão de uma taxa de período de tempo maior para uma taxa de período de tempo menor : taxa anual em taxa trimestral, taxa semestral em taxa mensal, etc. 3 . Conversões de taxas de juros:

24. Vamos, neste caso aplicar a seguinte fórmula: onde: i e = taxa equivalente; i q = taxa conhecida a ser convertida; n = número de períodos contidos no período da taxa de juros menor. Exemplo: Converter uma taxa de 40% a.a. em taxa quadrimestral. => 11,87% a.q. 3 . Conversões de taxas de juros:

25. Exercício Calcular a taxa equivalente mensal de uma taxa de: 1. 100% a.a.; 2. 82% a.a.; 3. 28% a.s. e 28% a.a.; 4. 28% a.a. ; 5. 32% a.t. 3 . Conversões de taxas de juros:

26. Exercícios Determinar o montante no final de 10 meses, resultante da aplicação de um capital de $ 100.000,00 a taxa de 3,75% a.m. R: $ 144.504,39 Uma pessoa empresta $ 80.000,00 hoje para receber $ 507.294,46 no final de 2 anos. Calcular as taxas mensal e anual desse empréstimo. R: 8% a.m. ou 151,817% a.a. Sabendo-se que a taxa trimestral de juros cobrada por uma institução finaceira é de 12,486%, determinar qual o prazo em que um empréstimo de $ 20.000,00 será resgatado por $ 36.018,23. R: 5 trimestres ou (15 meses).

27. Quanto devo aplicar hoje, a taxa de 51,107% a.a. para ter $ 1.000.000,00 no final de 19 meses. R: $ 520.154,96. Em que prazo uma aplicação de $ 374.938,00 a taxa de 3.25% a.m., gera um resgate de $ 500.000,00 R: 9 meses.

28. 4 . Fluxo de Caixa: 4.1 Conceito de Fluxo de caixa A resolução de problemas de matemática financeira torna-se muito mais fácil quando utilizamos o conceito de fluxo de caixa.Um fluxo de caixa é uma representação gráfica de uma série de entradas (recebimentos) e saídas (pagamentos). As saídas são representadas por uma seta para baixo e as entradas por uma seta para cima. Exercício: Representar as seguintes entradas e saídas num diagrama de fluxo de caixa: 0 - 1000 0 + 1000 3 + 1800 -200 5 + 1500 4 + 800 2 + 800 -500 1 Entrada ($)‏ Saída ($)‏ Período

29. 4 . Fluxo de Caixa: O fluxo acima pode ser simplificado, de acordo com a representação abaixo: 4.2 Métodos de avaliação de fluxos de caixa Os métodos mais utilizados de avaliação de fluxos de caixa são: (a) o método do valor presente líquido (VPL) e (b) o método da taxa interna de retorno (TIR), que veremos mais a frente, na seção avaliação de investimentos. 4.2.1 Cálculo do valor de um fluxo de caixa São definidas algumas regras básicas para o cálculo do valor númerico de um fluxo de caixa: (i) o fluxo deve ser inicialmente simplificado, (ii) o fluxo deve ser calculado em um determinado período de tempo, isto é, todas as entradas e saídas devem ser trazidas para uma mesma data e (iii) as entradas e saídas devem ser trazidas para este período de tempo. (+)‏ (-)‏ 1 3 4 5 2 1 3 4 5 2 0

30. 4 . Fluxo de Caixa: Exemplo: Calcular o seguinte fluxo de caixa, FC (0) , considerando-se uma taxa de juros de 5% a.p.: Descontando todas as saídas e entradas e trazendo para o momento 0, temos: FC(0) = -1000 + 200/(1+0,05) 1 + 800/(1+0,05) 2 + 1600/(1+0,05) 3 + 1400/(1+0,05) 4 + 1400/(1+0,05) 5 = -1000 + 190,47 + 725,62 + 1382,14 + 1151,78 + 1096,93 = $ 3546,94 1 3 4 5 2 1000 200 800 1400 1600 1400

31. 4 . Fluxo de Caixa: Exercício: Calcular o seguinte fluxo de caixa, FC (3) , considerando-se uma taxa de juros de 10% a.p.: FC (3) = 1 3 4 5 2 500 300 400 600 500 800

32. 5 . Séries uniformes: 5.1 Cálculo de uma série uniforme postecipada Podemos entender uma série uniforme de pagamentos como uma série de pagamentos que possui as seguintes características: (i) os valores dos pagamentos são todos iguais; e (ii) consecutivos, como ilustrado abaixo: (a)‏ Fig. 2.3: Série uniforme postecipada (a) e antecipada (b). (b)‏ 5.1 Série postecipada e antecipada Numa série postecipada (a) o primeiro pagamento ocorre a partir do primeiro período, enquanto uma série antecipada (b) é caracterizada pelo fato do primeiro pagamento ocorrer no início do período. 1 3 4 5 2 300 300 300 300 300 0 1 3 4 5 2 500 500 500 500 500 0 500

33. 5.1 Cálculo do montante S de uma série uniforme postecipada Consideremos uma série uniforme postecipada, descontada mensalmente a uma taxa de 4%, como mostrado abaixo: 5 . Séries uniformes: É possível calcular o valor futuro da série com o uso de fórmulas já conhecidas: S 1 = 100 x (1,04) 4 = 100 x 1,16986 = 116,98 S 2 = 100 x (1,04) 3 = 100 x 1,12486 = 112,49 S 3 = 100 x (1,04) 2 = 100 x 1,08160 = 108,16 S 4 = 100 x (1,04) 1 = 100 x 1,04000 = 104,00 S 5 = 100 x (1,04) 0 = 100 x 1,10000 = 100,00 S t = .................................................. = 541,63 Assim, podemos concluir que, o montante de 5 aplicações, mensais e consecutivas aplicadas a um taxa de 4% a.m. acumula um montante de $ 541,63. 1 3 4 5 2 100 100 100 100 100 0 S =

34. 5 . Séries uniformes: Sabemos que S t = S 1 + S 2 + S 3 + S 4 + S 5 , substituindo S 1 , S 2 , S 3 ..., por seus respectivos valores temos: S t = 100 x (1,04) 4 + 100 x (1,04) 3 + 100 x (1,04) 2 + 100 x (1,04) 1 + 100 x (1,04) 0 . Como o fator 100 é comum a todos os termos, podemos agrupar a expressão acima: S t = 100 { (1,04) 0 + (1,04) 1 + (1,04) 2 + (1,04) 3 + (1,04) 4 } (equação 10)‏ Como a série entre chaves, acima, representa a soma de uma progressão geométrica de razão 1,04, podemos aplicar a seguinte fórmula, que nos fornece a soma dos termos de uma PG, com a 1 = (1,04) 0 =1, q = 1,04 e n = 5. Transformando a equação 10 com a inclusão da fórmula da soma de uma PG, como mostrado acima, obtemos: (equação 11)‏

35. 5 . Séries uniformes: Substituindo os termos genéricos na equação 11, obtemos: (equação 12)‏ onde: S = montante acumulado da série uniforme postecipada; A = valor das prestações; i = taxa de Juros e n = número de períodos ou prestações. A expressão é chamada, também, de maneira análoga, as séries simples, de fator de acumulação de capital , FAC . Assim, a série uniforme postecipada, mostrada no início da seção 5.1 poderia, também, ser calculada da seguinte forma: F = 100 x FAC (4%,5) = 100 x 5,41632 = $ 541,63 5.2 Cálculo do valor das prestações A, conhecido o montante acumulado S Podemos transformar a equação 12, colocando A em função de S: (equação 13)‏ A expressão é denominada de fator de formação de capital (FFC), encontando-se tabelada, como anexo, na maioria dos livros de matemática financeira.

36. 5.3 Cálculo do valor presente P de uma série uniforme postecipada Consideremos uma série uniforme antecipada do tipo: O valor presente P, pode ser calculado através da fórmula: (equação 14)‏ onde: P = valor presente das prestações da série postecipada; A = valor das prestações; n = número das prestações. O fator é denominado fator de valor atual, FVA, sendo encontrado, como anexo, em tabelas em livros de matemática financeira. 5 . Séries uniformes: 1 3 4 2 A A A A 0 P = n A

37. Exercício Calcular o valor atual de uma série de 12 prestações mensais, iguais e consecutivas de $150, capitalizadas a uma taxa mensal de $ 5% ao mes. P = A x FVA (5%,12) = 150 x 8,86325 = $ 1.329,48 5.3 Cálculo do montante S de uma série uniforme antecipada Consideremos uma série uniforme antecipada do tipo: O montante S pode ser calculado através da fórmula: (equação 15)‏ onde: S = montante acumulado no final do período; A = valor das prestações; i = taxa de juros. 5 . Séries uniformes: 1 3 4 2 A A A A A 0 F = n A

38. 5 . Séries uniformes : Note, que a expressão entre parentesis, indicada na equação 15, nada mais é que o fator de acumulação de capital, FAC, para séries uniformes postecipadas, mostrado na equação 12, na p. 35 do nosso texto.E, portanto, a equação 15 pode ser escrita da seguinte maneira: (equação 16)‏ Exemplo: Quanto terei de aplicar mensamente, a partir de hoje, para acumular no final de 36 meses, um montante de $ 100.000,00, sabendo-se que a taxa de juros contratada é de 34,489% ao ano, que as prestações são iguais e consecutivas e a primeira prestação é depositada no período 0. Vamos, inicialmente, transformar a taxa anual em taxa mensal: 1 2 6 3 4 5 0 35 F=$ 100.000 A =

39. Transformando a equação 16, e colocando A (prestação) em função de S (valor futuro acumulado das prestações) obtemos: Aplicando a fórmula acima, com S = $ 100.000,00, i = 2,5% a.m. e n = 36, obtemos: A = 100.000 x 1/(1+0,025) x FFC (2,5%,36) = 100.000 x 0,97560 x 0,01745 = $ 1.702,42 5.4 Cálculo do valor presente P de uma série uniforme antecipada Consideremos uma série uniforme antecipada do tipo: O valor presente P pode ser calculado através da expressão: (equação 17)‏ 5 . Séries uniformes: 1 2 6 3 4 5 0 35 P = A =$100

40. Exemplo: Determinar o valor presente do financiamento de um bem financiado em 36 prestações iguais de $ 100,00, sabendo-se que a taxa de juros cobrada é de 3,0% a.m. e que a primeira prestação é paga no ato da assinatura do contrato. Fazendo uso da equação 17: P = A x (1+i) x FVA (3,0,%,36) = 100 x (1,03) x 21,83225 = $ 2248,72 5.5 Cálculo da prestação A, dado o valor presente P de uma série uniforme antecipada Nestas condições, o valor A da prestação pode ser calculado a partir da transformação da equação 17: (equação 18)‏ 5 . Séries uniformes:

41. Exemplo: Um terreno é colocado a venda por $ 50.000,00 a vista ou em 24 prestações mensais sendo a primeira prestação paga na data do contrato. Determinar o valor de cada parcela, sabendo-se que o proprietário está cobrando uma taxa de 3,5 % a.a. pelo financiamento. Aplicando a equação 18, obtemos: 5 . Séries uniformes: 1 2 6 3 4 5 0 23 P =$ 50.000,00 A =$

42. Exercícios 1. Um investidor depositou, anualmente, $ 1000,00 numa conta de poupança, em nome de seu filho, a juros de 6% a.a. O primeiro depósito foi feito no dia em que seu filho completou 1 ano e o último quando este completou 18 anos. O dinheiro ficou depositado até o dia em que completou 21 anos, quando o montante foi sacado. Quanto recebeu seu filho. R: $ 36.809,24 Quanto deverá ser aplicado, a cada 2 meses, em um fundo de renda fixa, a taxa de 5% ao bimestre, durante 3 anos e meio, para que se obtenha, no final deste prazo, um montante de $ 175.000,00. R: $ 4.375,00 Qual é o montante obtido no final de 8 meses, referente a uma aplicação de $ 500,00 por mes, a taxa de 42,5776% ao ano. R: $ 4.446,17

43. Quantas aplicações mensais de $ 500,00 são necessárias para se obter um montante de $ 32.514,00, sabendo-se que a taxa é de 3,00% a.m., e que a primeira aplicação é feita no ato da assinatura do contrato e a última 30 dias antes do resgate daquele valor. R: 36 aplicações. O Sr. Laerte resolveu fazer 12 aplicações mensais, como segue: a) 6 prestações iniciais de $ 1000 cada uma; b) 6 prestações restantes de $ 2000,00 cada uma. Sabendo-se que esta aplicação está sendo remunerada a 3,0% a.m., calcular o saldo acumulado de capital mais juros que estará a disposição do Sr. Laerte no final do prazo de aplicação. R:2.066,04

44. 6. Avaliação de investimentos 6.1 Métodos de retorno de investimento Existem 3 métodos, que são tradicionamente utilizados para a avaliação de investimentos: (a) o método do valor presente líquido (VPL), (b) o método da taxa interna de retorno (TIR) e (c) o método do pay back ou do tempo de retorno do investimento. 6.1 Método do valor presente líquido O método do valor presente líquido baseia-se no cálculo do valor presente de um fluxo de caixa que envolve saídas (investimento) e entradas (receitas geradas por este investimento). É a seguinte a fórmula que permite calcular o valor presente líquido (VPL) de um fluxo de investimento. Dado um fluxo de caixa do tipo, descontado a uma taxa i: O valor presente deste fluxo pode ser calculado como: (equação 19)‏ 1 3 4 2 FC 1 FC 2 FC 4 FC 3 0 n FC n FC 0

45. Para que um investimento seja economicamente viável, o valor presente do fluxo de caixa deve ser positivo, isto é o valor presente das entradas (receitas geradas por este investimento) deve superar o valor presente das saídas (investimentos e despesas relativas ao investimento). Exemplo : Considere o fluxo de caixa mostrado na seção 4.1, descontado a uma taxa de 10% a.a.: Descontando o fluxo de caixa FC (0) utilizando a equação 19, obtemos: VPL = 300/(1,1) + 800 /(1,1) 2 + 1000 /(1,1) 3 + 1500 /(1,1) 4 + 1600 /(1,1) 5 -1000= $ 2703,10 6. Avaliação de investimentos Quadro 6.1: Fluxo de caixa de um dado investimento: + 1800 + 1500 + 1000 + 800 + 800 0 Receitas ($)‏ FC 5 FC 4 FC 3 FC 2 FC 1 FC 0 FC - 1000 - 1000 0 + 1000 3 + 1600 -200 5 + 1500 4 + 800 2 + 300 -500 1 FCL ($)‏ Investimentos ($)‏ Período

46. No caso do exemplo anterior, o investimento é economicamente viável, uma vez que o valor presente líquido deste investimento é positivo, isto é, a soma das entradas (receitas) supera o valor das saídas (investimento e despesas). 6.2 Método da taxa interna de retorno A taxa interna de retorno (TIR) é a taxa que equaliza as entradas e saídas de um projeto de investimento. A equação que fornece a taxa interna de retorno, pode ser escrita da seguinte forma: (equação 20)‏ Assim, existe pelo menos uma taxa de juros i, que iguala FC 0 à somatória dos FC j . A taxa de juros que ¨zera¨ o fluxo de caixa é a própria taxa interna de retorno e representa a rentabilidade de um projeto de investimento. Na prática, o cálculo da taxa interna de retorno é feito através de um processo interativo, isto é, calculando-se o valor presente líquido do fluxo de caixa e observando-se a taxa, na qual ocorre a inversão do sinal do VPL do projeto de investimento. 6. Avaliação de investimentos

47. Exercício: Determinar a TIR do fluxo de caixa mostrado na figura 6.1. Calculemos o VPL deste fluxo de caixa para diferentes taxas de juros: VPL (10%) = $ 2703,19 VPL (20%) = $ 1750,64 VPL (30%) = $ 1115,43 VPL (40%) = $ 674,84 VPL (50%) = $ 358,85 VPL (60%) = $ 125,61 VPL (70%) = $ -50,89 Sabemos, portanto, que existe uma inversão de sinal no intervalo situado entre 60% e 70% e que a TIR está situada neste intevalo. Através de sucessivas aproximações obtemos uma TIR de 66,8% . 6. Avaliação de investimentos

48. 6. Avaliação de investimentos 6.2 Método do ¨Pay-back¨ ou do tempo de retorno de um investimento A viabilidade economica de um projeto de investimento pode se determinada, comparando-se o tempo de retorno do projeto com a vida útil dos ativos que compõem este investimento. Para que um projeto possa ser considerado economicamente viável, o tempo de retorno do projeto (em anos, meses ou qualquer outra unidade de tempo) deve ser inferior a vida util de um equipamento, ferramental, etc., por exemplo, que faz parte do investimento. Na prática, o tempo de retorno de um investimento é calculado através do fluxo de caixa descontado de um projeto de investimento. Considere o fluxo de caixa da figura 6.1. Observe, que no fluxo de caixa acumulado (coluna 7) existe uma inversão de sinal entre o 2o. e o 3o. ano. Isto significa que o tempo de retorno do projeto é superior a dois porém inferior a 3 anos. Aplicando uma regra de tres, proporcionalmente ao valor –66,12 do final do 2o. ano e 685,2 do final do 3o.ano, obtemos um tempo de retorno para este projeto de 2,1 anos. Quadro 6.2: Fluxo de caixa de um investimento:

49. 6. Avaliação de investimentos Assim, se a vida útil do equipamento for de 10 anos (suponhamos que este investimento se refira, por exemplo a aquisição de um caminhão) o projeto pode ser considerando viável, uma vez que este projeto trouxe um retorno num prazo inferior a vida útil deste bem.

50. 7. Desconto Simples (Bancário ou comercial)‏ 7.1 Conceituação A operação de desconto é realizada quando se conhece o valor futuro , também conhecido como valor nominal , valor de face ou valor de resgate . Entende-se desconto como a diferença entre o valor de resgate de um título e seu valor presente na data de operação, ou seja, D = S – P (equação 21)‏ onde, D representa o valor monetário do desconto, S o valor futuro ou valor de face e P o valor presente ou valor creditado ou pago ao titular. Assim como no caso dos juros, o valor do desconto também está associado a uma taxa e a determinado período de tempo. É frequente a confusão entre taxa de juros e desconto. Repare que a taxa de juros incide sempre sobre o montante do período anterior (juros compostos) ou sobre o principal ou capital inicial (juros simples) e no desconto a taxa refere-se, sempre, ao seu montante ou valor futuro. 7.2 Desconto simples ou bancário Desconto simples é aquele, no qual a taxa de desconto incide sobre o montante ou valor futuro S. É utilizado de maneira ampla no Brasil nas chamadas operações realizdas pelos bancos e chamadas de ¨desconto de duplicatas¨.

51. 7. Desconto Simples (Bancário ou comercial) O desconto é obtido multiplicando-se o seu valor de resgate F , pela taxa de desconto d (taxa de juros paga pela instituição financeira), e pelo prazo a transcorrer até seu vencimento, n ou: D = F x d x n (equação 21)‏ O valor presente P, ou de antecipação, pode ser calculado subtraindo-se do valor de resgate S, o desconto D, ou: P = F - D (equação 22)‏ Exemplo: Qual é o valor de desconto simples de um título de $ 1.000,00 com vencimento de 120 dias a taxa de 3,0% a.m. e o valor a receber na data da antecipação. Aplicando diretamente a equação 21, obtemos: D = 1000 x 4 x 0,03 = $ 120,00 O valor a receber pelo aplicador será de : P = 1000 – 120 = $ 880,00

52. 7.2 Desconto composto Desconto composto é aquele, no qual a taxa de desconto incide sobre o montante ou valor futuro S, deduzido dos descontos acumulados até o período imediatamente anterior. É obtido em função de cálculos exponenciais, e praticamente não é utilizado em nenhum país do mundo. O valor líquido de um título calculado por este critério, por um prazo igual a n períodos unitários, é dado pela expressão: P = F (1 – d) n (equação 23)‏ Exemplo: Uma duplicata de $ 10.000,00 com 90 dias para seu vencimento é descontada a uma taxa de 3,0% a.m. de acordo com o conceito de juros compostos. Calcular o valor líquido a ser creditado na conta e o valor do desconto concedido. A aplicação direta da equação 23 fornece o valor descontado (presente) do título: P = 10000 (1 – 0,03) 3 = 10000 x 0,91267 = $ 9126,73 O desconto é a diferença entre o valor de face (futuro) e o valor descontado e portanto D = 10000,00 – 9126,73 = $ 873,27 7. Desconto Simples (Bancário ou comercial)

53. Exercícios sobre Descontos Qual o valor atual de um título de valor de resgate de $ 90.000,00 com 4 meses a vencer, sabendo-se que a taxa de desconto é de 3,25% ao mes, com a) desconto simples e desconto composto. R: a) $ 78.300,00 ; b) 78.852,12 Sabendo-se que o valor líquido creditado na conta de umcliente foi de $ 57.170,24, correspondente a um título de $ 66.000,00 a taxa de 5,0% a.m. Determinar o prazo a decorrer até o vencimento deste título com a) juros simples e juros compostos. R: a) 2,67 meses e b) 2,8 meses.