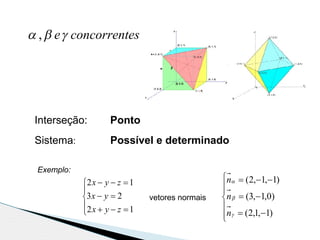
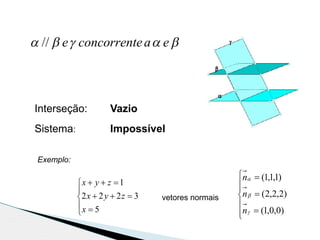
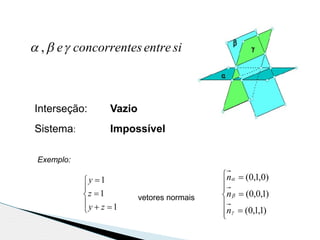
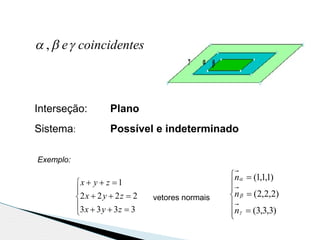
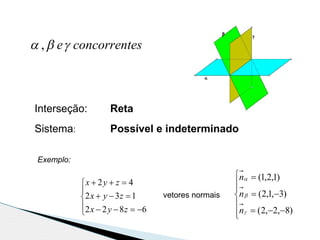
1) O documento discute os conceitos de interseção de planos, resolução de sistemas de equações e métodos para resolução de sistemas de equações lineares. 2) São apresentados exemplos numéricos para ilustrar os conceitos de interseção de três planos e resolução de sistemas de equações por substituição e adição ordenada. 3) As informações são relevantes para estudantes do 11o ano sobre geometria analítica e resolução de sistemas de equações lineares.

1. Geometria
11º Ano
Interseção de 3 Planos
Abril 2015 José Salvador

2.  ////
Interseção:
Sistema:
Exemplo:








5333
3222
1
zyx
zyx
zyx
vetores normais









)3,3,3(
)2,2,2(
)1,1,1(



n
n
n
Vazio
Impossível

3. Interseção:
Sistema:
Exemplo:








5
3222
1
x
zyx
zyx
vetores normais









)0,0,1(
)2,2,2(
)1,1,1(



n
n
n
Vazio
Impossível
 eaeconcorrente//

4. Interseção:
Sistema:
Exemplo:








1
1
1
zy
z
y
vetores normais









)1,1,0(
)1,0,0(
)0,1,0(



n
n
n
Vazio
Impossível
sientreesconcorrente ,

5. Interseção:
Sistema:
Exemplo:








3333
2222
1
zyx
zyx
zyx
vetores normais









)3,3,3(
)2,2,2(
)1,1,1(



n
n
n
Plano
Possível e indeterminado
escoincidente ,

6. Interseção:
Sistema:
Exemplo:








6822
132
42
zyx
zyx
zyx
vetores normais









)8,2,2(
)3,1,2(
)1,2,1(



n
n
n
Reta
Possível e indeterminado
esconcorrente ,

7. Interseção:
Sistema:
Exemplo:








12
23
12
zyx
yx
zyx
vetores normais









)1,1,2(
)0,1,3(
)1,1,2(



n
n
n
Ponto
Possível e determinado
esconcorrente ,

8. Geometria
11º Ano
Resolução de Sistemas de
Equações

9. Princípio da Substituição








7734
12
5235
zyx
zyx
zyx









77)12(34
12
52)12(35
zzxx
zxy
zzxx









773364
12
523365
zzxx
zxy
zzxx









442
12
2
zx
zxy
zx









22
12
2
zx
zxy
zx

10. Princípio da Substituição









222
12
2
zz
zxy
zx









03
12
2
z
zxy
zx









0
12
20
z
zxy
x









0
10)2(2
2
z
y
x









0
5
2
z
y
x
   0,5,2,, zyx









22
12
2
zx
zxy
zx

11. Método de Adição Ordenada
 
 
 







37734
212
15235
zyx
zyx
zyx
2
3336
5235
)2(3)1(




zx
zyx
zyx
25
7734
5235
)3()1(




zx
zyx
zyx
CA
06
25
2
)5()4(




z
zx
zx
 
 
 








525
42
15235
zx
zx
zyx

12. Método de Adição Ordenada
   0,5,2,, zyx









06
2
5235
z
zx
zyx









0
2
5235
z
zx
zyx









0
20
5235
z
x
zyx









0
2
5)0(23)2(5
z
x
y









0
5
2
z
y
x