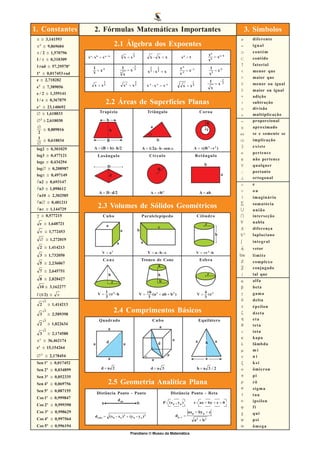
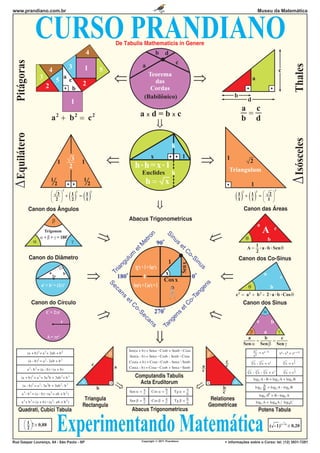
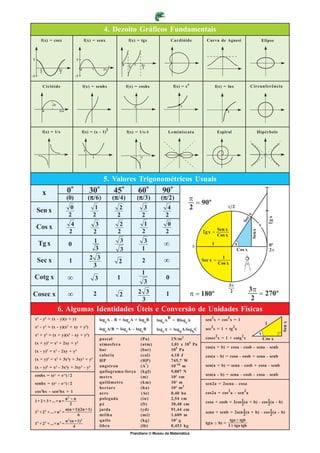
1) O documento apresenta fórmulas matemáticas importantes como áreas de figuras planas, volumes de sólidos geométricos e identidades trigonométricas. 2) Inclui também gráficos de funções como seno, cosseno e exponencial, além de figuras geométricas como elipse, hipérbole e círculo. 3) Por fim, fornece tabelas com valores trigonométricos e conversões de unidades físicas como Pascal, bar e caloria.

1. EXPERIMENTANDO
Para Alunos de Colegial e Cursinho
Greco © Museu da Matemática Prandiano
Teorema dos Cossenos
´
MATEMATICA
w w w. p r a n d i a n o . c o m . b r
Prandiano © Museu da Matemática

2. 1. Constantes 2. Fórmulas Matemáticas Importantes 3. Símbolos
diferente
2.1 Álgebra dos Expoentes igual
contém
contido
fatorial
menor que
maior que
menor ou igual
maior ou igual
adição
2.2 Áreas de Superfícies Planas subtração
divisão
Trapézio Triângulo Coroa
multiplicação
proporcional
aproximado
se e somente se
implicação
existe
pertence
Losângulo Círculo Retângulo
não pertence
qualquer
portanto
ortogonal
e
ou
imaginário
2.3 Volumes de Sólidos Geométricos somatória
união
Cubo Paralelepípedo Cilindro interseção
nabla
diferença
laplaciano
integral
vetor
limite
Cone Tronco de Cone Esfera complexo
conjugado
tal que
alfa
beta
gama
delta
épsilon
2.4 Comprimentos Básicos dzeta
Quadrado Cubo Equilátero eta
teta
iota
kapa
lâmbda
mi
ni
ksi
ômicron
pi
2.5 Geometria Analítica Plana rô
sigma
Distância Ponto - Ponto Distância Ponto - Reta tau
ípsilon
fi
qui
psi
ômega
Prandiano © Museu da Matemática

3. 4. Dezoito Gráficos Fundamentais
f(x) = cosx f(x) = senx f(x) = tgx Cardióide Curva de Agnesi Elipse
Ciclóide f(x) = senhx f(x) = coshx f(x) = ex f(x) = lnx Circunferência
2
f(x) = 1/x f(x) = (x - 1) f(x) = 1/x-1 Leminiscata Espiral Hipérbole
5. Valores Trigonométricos Usuais
o o o o o
x 0 30 45 60 90
(0) 
(/6) 
(/4) 
(/3) 
(/2)
Sen x
Cos x
Tg x 0
Sec x 1 2
Cotg x 1 0
Cosec x 2 1
6. Algumas Identidades Úteis e Conversão de Unidades Físicas
x2 - y2 = (x - y)(x + y) logcA . B = logcA + logcB
B 2 2
sen x + cos x = 1
logc A = Blogc A
x - y = (x - y)(x + xy + y )
3 3 2 2
logc A/B = logcA - logcB sec2x = 1 + tg2x
logcA = log bA/logb C
x + y = (x + y)(x - xy + y )
3 3 2 2
pascal (Pa) 1N/m 2 cosec2x = 1 + cotg2x
(x + y) = x + 2xy + y
2 2 2
atmosfera (atm) 1,01 x 105 Pa
cos(a + b) = cosa . cosb - sena . senb
(x - y)2 = x2 - 2xy + y2 bar (bar) 105 Pa
caloria (cal) 4,18 J cos(a - b) = cosa . cosb + sena . senb
(x + y)3 = x3 + 3x2y + 3xy2 + y3 HP (HP) 745,7 W
o
(x - y)3 = x3 - 3x2y + 3xy2 - y3 angstron (A ) 10 -10 m sen(a + b) = sena . cosb + cosa . senb
quilograma-força (kgf) 9,807 N
coshx = (ex + e-x) / 2 sen(a - b) = sena . cosb - cosa . senb
metro (m) 102 cm
senhx = (e x - e-x) / 2 quilômetro (km) 10 3 m sen2a = 2sena . cosa
hectare (ha) 10 4 m 2
cos hx - sen hx = 1 cos2a = cos2a - sen 2a
2 2
acre (Ac) 0,40 ha
polegada (in) 2,54 cm
pé (ft) 30,48 cm cosa + cosb = 2cos (a + b) . cos (a - b)
jarda (yd) 91,44 cm
sena + senb = 2sen (a + b) . cos (a - b)
milha (mi) 1.609 m
quilo (kg) 10 3 g
tg(a b) =
libra (lb) 0,453 kg
Prandiano © Museu da Matemática

4. SOBRE O CURSO
Experimentando Matemática foi desenvolvido pela Prandiano, supervisi-
onado pelo prof. Aguinaldo Prandini Ricieri, com o propósito de reforçar a
Matemática dos alunos do colegial e do cursinho. Para isso, foram projetados e
construídos centenas de experimentos, alguns únicos em todo o mundo, que
permitem ao aluno visualizar e aprender os fundamentos da Matemática de for-
ma lúdica. Isso, somado às indispensáveis deduções teóricas, exercitadas na so-
lução de centenas de problemas de vestibular e questões do dia-a-dia, permite,
de uma vez por todas, que o aluno pratique Matemática e se interesse por ela.
MUSEU DA MATEMÁTICA
Esse Curso de Matemática Experimental e Dedutiva é acessível a todos e
acontece em (1 + 11) aulas muito divertidas no Museu da Matemática.
Escolha uma das três datas (D1, D2 ou D3) e venha
participar de 01 aula (6 horas) demonstrativa gratuita.
Gostando, você poderá inscrever-se no Curso (+11 aulas*).
(*Aulas aos Domingos às 07:30h - Valor: R$ 600,00 ou 6 x R$ 100,00 com cheques pré-datados)
D1: Dia 27 de Agosto/sábado (14:00h) ou
D2: Dia 28 de Agosto/domingo (08:00h) ou
D3: Dia 03 de Setembro/sábado (14:00h)
(Sujeito não Haver Lugares. Trazer Folhas de Papel A4.)
Descubra como é prático e fácil aprender Matemática.
Rua Gaspar Lourenço, 64 - Vila Mariana (Metrô Ana Rosa - SP)
Início do Curso: 04 / Setembro / 07:30h (Domingo) (tel. (12) 3931-7281)
Prandiano © Museu da Matemática

5. www.prandiano.com.br Museu da Matemática
Rua Gaspar Lourenço, 64 - São Paulo - SP Copyright C 2011 Prandiano + informações sobre o Curso: tel. (12) 3931-7281