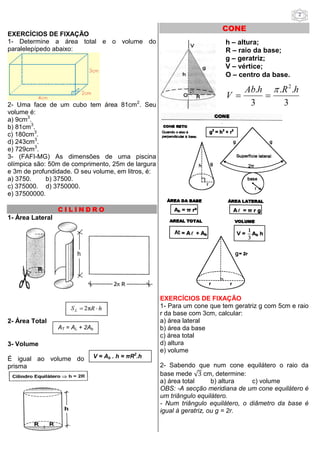
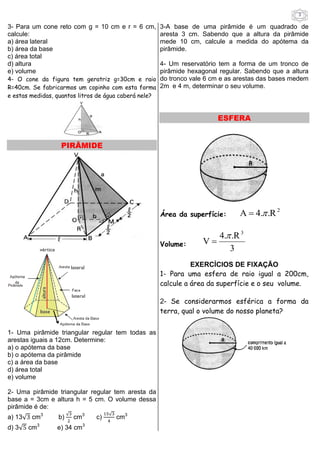
1. O documento apresenta conceitos e fórmulas de geometria espacial relacionados a sólidos como prisma, paralelepípedo, cubo, cilindro, cone, pirâmide e esfera. 2. Inclui exemplos de cálculo de áreas, volumes e outras grandezas geométricas desses sólidos. 3. Propõe exercícios para fixação dos conceitos apresentados.

1. 1
GEOMETRIA ESPACIAL
3º ANO
VESTIBULAR 2012
Prof. J.PORTAL
jonaspo@hotmail.com
GUARDE NA MENTE:
1 m3= 1000 litros 1cm3 = 1ml
1 litro = 1 dm3 = 1000 cm3
ALTURA E ÁREA DO TRIÂNGULO EQUILÁTERO
Área do Círculo=
FÓRMULA MUITO USADA:
a2 = b2 + c2 (Teorema de Pitágoras)
POLIEDRO: Sólidos limitados por superfícies
planas poligonais, nas quais podemos destacar os
seguintes elementos:
E S T U D O D O S P R I S M A S
1- Classificação e elementos
Aresta da Base (  ) – É o lado do polígono da
base.
Aresta Lateral (L) – É o lado de uma face lateral.
Altura (h) – É a distância entre os planos das bases.
Vértices – São as quinas (interseção entre duas arestas)
Área lateral (AL)
ÁREAS IMPORTANTES
Área da Base (Ab)
Representa a área do polígono da base.
Área lateral (AL)
Representa a soma das áreas das faces laterais.
Área total (At ):
VOLUME: V = Ab.H
APLICAÇÕES
1- Qual o valor da altura e da área de um
triângulo equilátero cujo lado mede 6cm?
2– Um prisma quadrangular regular tem 7cm de
aresta lateral e 5 cm de aresta da base. Calcular:
a) área da base
b) área lateral
c) área total
d) volume
3- um prisma triangular regular apresenta 9cm de
aresta lateral e 4 cm de aresta da base. Calcular
a) área da base
b) área lateral
c) área total
d) volume
PARALELEPÍPEDO
Fórmulas:
Diagonal da face: d = √
Diagonal do Paralelepípedo: D = √
Área total: AT = 2(ab + ac + bc)
Volume: V = a.b.c
Exemplo: Para encher uma caixa d´água de 3m de
comprimento por 2m de largura e 2 m de
profundidade, quanto litros de água são
necessários?
CUBO
Fórmulas:
Diagonal: D = a√
Área: AT = 6a2
Volume: V = a3
Exemplo: Uma caixa cúbica tem 2 m de aresta.
Determine a diagonal da caixa, a área total e a sua
capacidade, em litros.
l
l
l
h
풉 풍
√ퟑ
ퟐ
풆 푨 풍ퟐ √ퟑ
ퟒ
R
A = 휋R2
VÉRTI
CE
FACE
AREST
A
Altura (c)
Largura (b)
Comprimento (a)
a
a
a

2. 2
EXERCÍCIOS DE FIXAÇÃO
1- Determine a área total e o volume do
paralelepípedo abaixo:
2- Uma face de um cubo tem área 81cm2. Seu
volume é:
a) 9cm3.
b) 81cm3.
c) 180cm3.
d) 243cm3.
e) 729cm3.
3- (FAFI-MG) As dimensões de uma piscina
olímpica são: 50m de comprimento, 25m de largura
e 3m de profundidade. O seu volume, em litros, é:
a) 3750. b) 37500.
c) 375000. d) 3750000.
e) 37500000.
C I L I N D R O
1- Área Lateral
2- Área Total
3- Volume
É igual ao volume do
prisma
CONE
EXERCÍCIOS DE FIXAÇÃO
1- Para um cone que tem geratriz g com 5cm e raio
r da base com 3cm, calcular:
a) área lateral
b) área da base
c) área total
d) altura
e) volume
2- Sabendo que num cone equilátero o raio da
base mede √ cm, determine:
a) área total b) altura c) volume
OBS: -A secção meridiana de um cone equilátero é
um triângulo equilátero.
- Num triângulo equilátero, o diâmetro da base é
igual à geratriz, ou g = 2r.
h
AT = AL + 2Ab
V = Ab . h = πR2.h
h – altura;
R – raio da base;
g – geratriz;
V – vértice;
O – centro da base.

3. 3
3- Para um cone reto com g = 10 cm e r = 6 cm,
calcule:
a) área lateral
b) área da base
c) área total
d) altura
e) volume
4- O cone da figura tem geratriz g=30cm e raio
R=40cm. Se fabricarmos um copinho com esta forma
e estas medidas, quantos litros de água caberá nele?
PIRÂMIDE
1- Uma pirâmide triangular regular tem todas as
arestas iguais a 12cm. Determine:
a) o apótema da base
b) o apótema da pirâmide
c) a área da base
d) área total
e) volume
2- Uma pirâmide triangular regular tem aresta da
base a = 3cm e altura h = 5 cm. O volume dessa
pirâmide é de:
a) 13√ cm3 b)
√
cm3 c)
√
cm3
d) 3√ cm3 e) 34 cm3
3-A base de uma pirâmide é um quadrado de
aresta 3 cm. Sabendo que a altura da pirâmide
mede 10 cm, calcule a medida do apótema da
pirâmide.
4- Um reservatório tem a forma de um tronco de
pirâmide hexagonal regular. Sabendo que a altura
do tronco vale 6 cm e as arestas das bases medem
2m e 4 m, determinar o seu volume.
ESFERA
Área da superfície:
2 A  4. .R
Volume:
3
4. .R
V
3 

EXERCÍCIOS DE FIXAÇÃO
1- Para uma esfera de raio igual a 200cm,
calcule a área da superfície e o seu volume.
2- Se considerarmos esférica a forma da
terra, qual o volume do nosso planeta?

4. 4
 ATIVIDADES – PROF.J.PORTAL
G.ESPACIAL
1. Qual o volume da caixa da figura abaixo?
2. Quantos litros de leite cabem na caixa da figura
abaixo?
3. A pirâmide de Quéops é conhecida como a Grande
Pirâmide do Egito. Sua base (quadrada) tem
aproximadamente 230 m de aresta e sua altura é de
147 m. Qual o volume dessa pirâmide?
4. A figura representa um tambor, desses que são
usados no transporte de óleo. O raio da sua base
mede 30 cm e a altura, 85 cm. Quantos litros de óleo
ele pode comportar aproximadamente?
5. Uma seringa tem a forma cilíndrica com 2 cm de
diâmetro por 8 cm de comprimento. Quando o êmbolo
se afastar 5 cm da extremidade da seringa próxima à
agulha, qual o volume, em mililitros, de remédio líquido
que a seringa pode conter?
6- Um produto é embalado em recipiente com
formato de cilindros retos. O cilindro A tem altura
20cm e raio da base 5cm. O cilindro B tem altura
10cm e raio da base de 10cm.
a) Em qual das duas embalagens gasta-se menos
material?
b) O produto embalado no cilindro A é vendido
a R$ 4,00 a unidade, e o do cilindro B a R$ 7,00 a
unidade. Para o consumidor, qual a embalagem
mais vantajosa?
7- Uma caixa de sapatos (com tampa) é
confeccionada com papelão e tem as medidas,
em centímetros, conforme a figura. Sabendo-se
que à área total da caixa são acrescentados 2%
para fazer as dobras de fixação. Qual o total de
papelão empregado na confecção da caixa, em
cm2?
8-(ENEM-2010) Dona Maria, diarista na casa da
família Teixeira, precisa fazer café para servir as
vinte pessoas que se encontram numa reunião na
sala. Para fazer o café, Dona Maria dispõe de
uma leiteira cilíndrica e copinhos plásticos,
também cilíndricos.
Com o objetivo de não desperdiçar café, a diarista
deseja colocar a quantidade mínima de água na
leiteira para encher os vinte copinhos pela
metade. Para que isso ocorra, Dona Maria
deverá:
a) encher a leiteira até a metade, pois ela tem um
volume 20 vezes maior que o volume do copo.
b) encher a leiteira toda de água, pois ela tem um
volume 20 vezes maior que o volume do copo.
c) encher a leiteira toda de água, pois ela tem um
volume 10 vezes maior que o volume do copo.
d) encher duas leiteiras de água, pois ela tem um
volume 10 vezes maior que o volume do copo.
e) encher cinco leiteiras de água, pois ela tem um
volume 10 vezes maior que o volume do copo.