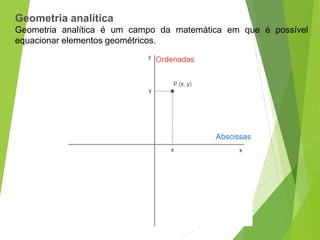
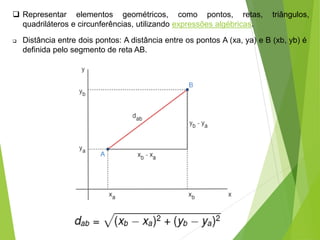
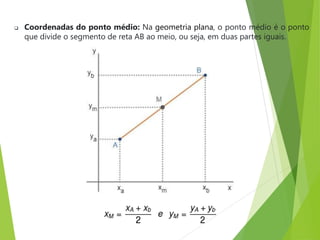
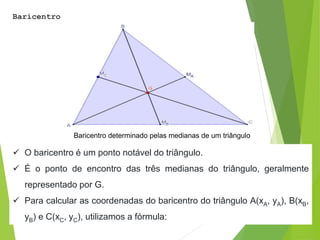
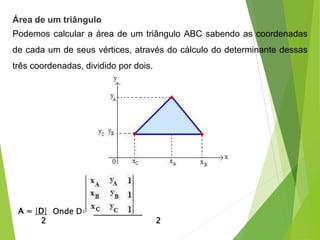
Geometria analítica permite representar elementos geométricos como pontos, retas e circunferências usando expressões algébricas. Pode-se calcular a distância entre pontos e determinar o ponto médio de um segmento de reta. Três pontos são colineares se o determinante formado por suas coordenadas for igual a zero.