1. Este documento é uma apostila de exercícios resolvidos de cálculo contendo dois capítulos: 2. O capítulo 1 trata de limites e continuidade, enquanto o capítulo 2 aborda derivadas. 3. A apostila foi produzida por Celton Ribeiro Barbosa e Prof. Gislan Silveira Santos para o Instituto Federal de Educação Ciência e Tecnologia da Bahia.

1. Celton Ribeiro Barbosa
Prof. Gislan Silveira Santos
Apostila de Exercícios Resolvidos de
Cálculo
Instituto Federal de Educação Ciência e Tecnologia da
Bahia
Programa de Educação Tutorial - PET
Tutor: Dr. Felizardo Adenilson Rocha

2. © 2014 Celton Ribeiro Barbosa ;Prof. Gislan Silveira
Santos & Instituto Federal de Educação Ciência e
Tecnologia da Bahia.
Programa de Educação Tutorial - PET
Tutor: Dr. Felizardo Adenilson Rocha
Qualquer parte desta publicação pode ser
reproduzida, desde que citada a fonte.
Dados Internacionais de Catalogação na Publicação
(CIP) Câmara Brasileira do Livro, BA, Brasil
Barbosa, Celton Ribeiro; Santos, Gislan Silveira.
Apostila de Exercícios Resolvidos de Cálculo. / Cel-
ton Ribeiro Barbosa ;Prof. Gislan Silveira Santos. –
Vitória da Conquista-BA: Instituto Federal de Edu-
cação Ciência e Tecnologia da Bahia. Ltda., 2014.
Bibliografia.
ISBN XXXX-XXXX-XX.
1. Matemática. 2. Cálculo 1.
APOSTILA EXERCÍCIOS DE CÁLCULO 2

3. SUMÁRIO
1 Limites e Continuidade 2
2 Derivadas 22
1

4. CAPÍTULO 1
LIMITES E CONTINUIDADE
1. O ponto P (2,ln2) pertencente à curva y = lnx.
(a) Se Q é o ponto (x,lnx), use sua calculadora para determinar o coefi-
ciente angular da reta secante PQ, com precisão de seis casas decimais,
para os seguintes valores de x:
(i) 1,5
(ii) 1,9
(iii) 1,99
(iv) 1,999
(v) 2,5
(vi) 2,1
(vii) 2,01
(viii) 2,001
(b) Usando os resultados da parte (a), estime o valor da inclinação da reta
tangente à curva no ponto P (2,ln2).
(c) Use a inclinação obtida na parte (b) para achar uma equação da reta
tangente à curva em P (2,ln2).
(d) Faça uma figura utilizando duas dessas retas secantes e a reta tan-
gente.
Resolução:
(a) A equação da reta é dada por:
(y − y0) = m(x − x0)
onde m - coeficiente angular da reta.
(x0, y0) - ponto onde se deseja encontrar a reta.
2

5. Limites e Continuidade
y0 = ln2 e x0 = 2
m =
y −ln2
x −2
=
lnx −ln2
x −2
=
ln(x/2)
x −2
(i) x = 1,5
m =
ln(1,5/2)
1,5−2
= 0,575364
(ii) x = 1,9
m =
ln(1,9/2)
1,9−2
= 0,512933
Os demais itens ficam a cargo do leitor.
x m
1,5 0,575364
1,9 0,512933
1,99 0,501254
1,999 0,500125
2,5 0,446287
2,1 0,487902
2,01 0,498754
2,001 0,499875
(b) Os valores se aproximão de 0,5.
(c)
y −ln2 = 0,5(x −2)
y = 0,5x +ln2−1
2. Calcule os limites a seguir, justificando cada passagem através das suas
propriedades.
(a)lim
t→0
1+
1
|t|
−
1
|t|
Resolução:
|t| =
t , se t > 0
−t , se t < 0
Para t > 0:
lim
t→0
1+
1
t
−
1
t
·
1+
1
t
+
1
t
1+
1
t
+
1
t
APOSTILA EXERCÍCIOS DE CÁLCULO 3

6. Limites e Continuidade
= lim
t→0
1+
1
t
−
1
t
1+
1
t
+
1
t
= lim
t→0
1
1+
1
t
+
1
t
= 0
Para t < 0:
lim
t→0
1+
1
−t
−
1
−t
·
1+
1
−t
+
1
−t
1+
1
−t
+
1
−t
= lim
t→0
1+
1
−t
−
1
−t
1+
1
−t
+
1
−t
= lim
t→0
1
1+
1
−t
+
1
−t
= 0
Como os limites laterais são iguais a resposta é 0.
(b)
(1/ x)−1
1− x
Resolução:
lim
x→1
1− x
x
1− x
= lim
x→1
(1− x)
(1− x) x
·
1+ x
1+ x
lim
x→1
(1− x)
(1− x) x(1+ x)
= lim
x→1
1
x(1+ x)
=
1
1(1+ 1)
=
1
2
3. Esboce os gráficos da função abaixo e , use-o para determinar os valores
de a para os quais lim
x→a
f (x) exista:
(a) f (x) =



1+ x , se x < −1
x2
, se −1 ≤ x < 1
2− x , se x ≥ 1
APOSTILA EXERCÍCIOS DE CÁLCULO 4

7. Limites e Continuidade
Resolução:
Figura 1.1: Gráfico de f(x)
4. Prove que o lim
x→0
|x|
x
não existe.
Dicas:
• Os limite só existe se os limites laterais forem iguais.
• |x| =
x , se x > 0
−x , se x < 0
5. Na teoria da relatividade, a massa de uma partícula com velocidade v é
m =
m0
1− v2/c2
, em que m0 é a massa da partícula em repouso e c, a
velocidade da luz. O que acontece se v → c−
?
Resolução
lim
x→c−
m0
1− v2/c2
=
m0
1−1
= ∞
6. Considere a função f definida por:
APOSTILA EXERCÍCIOS DE CÁLCULO 5

8. Limites e Continuidade
f (x) =
0 , se x é racional
1 , se x é irracional
Para todo a ∈ R, lim
x→a
f (x) não existe. Por quê?
Resolução:
Suponha que a ∈ Q, então f (a) = 0, logo lim
x→a
f (x) = 0
Por outro lado, a Q, então f (a) = 0, logo lim
x→a
f (x) = 1
Como a ∈ R , então lim
x→a
f (x), pois os limites laterais dessa função são
diferentes.
7. Calcule, se possível, os seguintes limites:
(g) lim
x→0
x +1− 1− x
3x
(l) lim
x→1
x3
−1
x2 −1
(o) lim
t→9
9− t
3− t
(t) lim
x→2
x4
−16
8− x3
(w) lim
x→7
2− x −3
x2 −49
Resolução:
(a)
lim
x→0
x +1− 1− x
3x
·
x +1+ 1− x
x +1+ 1− x
lim
x→0
(x +1)−(1− x)
3x( x +1+ 1− x)
lim
x→0
2x
3x( x +1+ 1− x)
=
2
3( x +1+ 1− x)
lim
x→0
x +1− 1− x
3x
=
2
3·(1+1)
=
2
6
=
1
3
(b)
lim
x→1
x3
−1
x2 −1
= lim
x→1
(x −1)(x2
+ x +1)
(x −1)(x +1)
lim
x→1
x2
+ x +1
x +1
=
12
+1+1
1+1
=
3
2
APOSTILA EXERCÍCIOS DE CÁLCULO 6

9. Limites e Continuidade
(c)
lim
t→9
9− t
3− t
·
3+ t
3+ t
lim
t→9
(9− t)(3+ t)
9− t
= 3+ 9 = 6
(d)
lim
x→2
x4
−16
8− x3
= lim
x→2
(x2
+4)(x2
−4)
(x −2)(−x2 −2x −4)
lim
x→2
(x2
+4)(x +2)(x −2)
(x −2)(−x2 −2x −4)
lim
x→2
(x2
+4)(x +2)
(−x2 −2x −4)
= −
8
3
(e)
lim
x→7
2− x −3
x2 −49
·
2+ x −3
2+ x −3
lim
x→7
4− x +3
(x +7)(x −7)(2+ x −3)
=
−(x −7)
(x +7)(x −7)(2+ x −3)
lim
x→7
=
−1
(x +7)(2+ x −3)
= −
1
56
8. Calcule, se existirem, os limites abaixo:
(a) lim
x→a
x − a
x2 − a2
com a > 0
(b) lim
x→a
x − a + x − a
x2 − a2
com a > 0
(c) lim
x→0
1+ x2 + x
m
− 1+ x2 − x
m
x
Resolução
(a)
lim
x→a
x − a
x2 − a2
= lim
x→a
x − a
(x − a)(x + a)
x − a
x − a x + a
·
x + a
x + a
x − a
x − a · x + a ·( x + a)
APOSTILA EXERCÍCIOS DE CÁLCULO 7

10. Limites e Continuidade
x − a
x + a ·( x + a)
=
0
2 a · 2a
= 0
(b)
lim
x→a
x − a + x − a
x2 − a2
lim
x→a
x − a + x − a
x − a x + a
lim
x→a
x − a
x − a · x + a
+ lim
x→a
x − a
x − a · x + a
lim
x→a
1
x + a
=
1
2a
(c)
lim
x→0
1+ x2 + x
m
− 1+ x2 − x
m
x
m = 1
lim
x→0
1+ x2 + x − 1+ x2 − x
x
= 2
m = 2
lim
x→0
1+ x2 + x
2
− 1+ x2 − x
m
2
= lim
x→0
2 x(2 1+ x2)
x
= 4
.
.
.
Resolvendo mais limites para outros valores de m é possível observar o
seguinte padrão: 2m
9. Mostre que o lim
x→0
x2
·cos(20πx) = 0.
−1 ≤ cos(2πx) ≤ 1
−x2
≤ x2
cos(2πx) ≤ x2
APOSTILA EXERCÍCIOS DE CÁLCULO 8

11. Limites e Continuidade
Pelo teorema do confronto:
lim
x→0
−x2
= 0, lim
x→0
x2
= 0
lim
x→0
x2
cos(2πx) = 0
10. Calcule, pelo Teorema do Confronto, lim
x→+∞
( x +1− x).
Resolução:
lim
x→+∞
( x +1− x)·
( x +1+ x
x +1+ x
= lim
x→+∞
1
x +1+ x
x +1 > x ⇒ x +1+ x > 2 x
lim
x→+∞
1
x +1+ x
<
1
2 x
0 < lim
x→+∞
1
x +1+ x
<
1
2 x
lim
x→∞
0 = lim
x→∞
1
2 x
= 0
Logo
lim
x→+∞
( x +1− x) = 0
11. A função sinal, denotada por sgn, está definida por
sgn(x) =



−1 , se x < 0
0 , se x = 0
1 , se x > 0
Dica:
APOSTILA EXERCÍCIOS DE CÁLCULO 9

12. Limites e Continuidade
Figura 1.2: Gráfico da função sinal
12. Considere a função f (x) =
x2
−1
|x −1|
Dica:
Figura 1.3: Gráfico da função f (x).
APOSTILA EXERCÍCIOS DE CÁLCULO 10

13. Limites e Continuidade
13. Seja g(x) =
x2
+ x −6
|x −2|
.
(a) Determine lim
x→2+
g(x) e lim
x→1−
g(x).
(b) Existe lim
x→1
g(x) ?
(c) Esboce o gráfico de g.
Dica:
Figura 1.4: Gráfico da função g(x).
14. Seja
h(x) =



x , se x < 0
x2
, se 0 < x ≤ 2
8− x , se x > 2
(a) Calcule, se existirem, os limites.
i. lim
x→0+
h(x) ii. lim
x→0−
h(x) iii. lim
x→0
h(x) iv. lim
x→2−
h(x) v. lim
x→2+
h(x)
vi. lim
x→2
h(x)
(b) Esboce o gráfico da função h.
Dica:
APOSTILA EXERCÍCIOS DE CÁLCULO 11

14. Limites e Continuidade
Figura 1.5: Gráfico da função h(x).
15. Determine os limites.
(a) lim
x→4
x −5
(x −4)2
Resolução:
lim
x→4
x −5 (Esse termo tende a -1)
(x −4)2 (Esse termo tende a 0)
y = (x −4)2
lim
y→0
−1
y
= −∞
(b) lim
x→0
cos(x)
x · sen (x)
Resolução:
lim
x→0
cos(x) (Esse termo tende a 1)
x · sen (x) (Esse termo tende a 0 )
APOSTILA EXERCÍCIOS DE CÁLCULO 12

15. Limites e Continuidade
y = x · sen x
lim
y→0
1
y
= ∞
16. Calcule os limites:
(a) lim
x→+∞
1+2+3+...+ x
x2
(b) lim
x→+∞
12
+22
+...+ x2
x3
Sugestão: Para (a)
x
k=1
k =
x(x +1)
2
e para (b)
x
k=1
k2
=
x(x +1)(2x +1)
6
.
Resolução:
(a) lim
x→+∞
x
k=1
k
x2
lim
x→+∞
x(x +1)
2x2
lim
x→+∞
1+ 1
x
2
(b) lim
x→+∞
x
k=1
k2
x3
lim
x→+∞
x(x +1)(2x +1)
6x3
lim
x→+∞
2x3
+3x2
+ x
6x3
lim
x→+∞
2+ 3
x + 3
x2
6
=
1
3
17. Calcule os seguintes limites no infinito:
(a) lim
x→+∞
3
x3 +2x −1
x2 + x +1
Resolução:
lim
x→+∞
3
x3(1+ 1
x2 − 1
x2 )
x2(1+ 1
x
+ 1
x2 )
lim
x→+∞
1+ 1
x2 − 1
x2
(1+ 1
x + 1
x2 )
= 1
APOSTILA EXERCÍCIOS DE CÁLCULO 13

16. Limites e Continuidade
(b) lim
x→+∞
x4 +2
x3
Resolução:
lim
x→+∞
x6( 1
x2 + 2
x6 )
x3
lim
x→+∞
x3
( 1
x2 + 2
x6 )
x3
= 0
(c) lim
x→−∞
x9
+1
x9 + x6 + x4 +1
lim
x→−∞
x9
(1+ 1
x9 )
x9(1+ 1
x3 + 1
x5 + 1
x9 )
= 1
18. Numa cidade, uma determinada notícia foi propagada de tal maneira que
o número de pessoas que tomaram conhecimento é dado por:
N(t)
1768
1+33e−10t
em que t representa o número de dias após ocorrer a notícia. Pergunta-
se:
(a) Quantas pessoas souberam a notícia de imediato?
(b) Determine lim
t→∞
N(t) e explique o seu resultado.
Dicas: o tempo tende a 0 no quesito (a)
19. Um tanque contém 5000 litros de água pura. Água salgada contendo 30 g
de sal por litro de água é bombeada para dentro do tanque a uma taxa de
25l/min.
(a) Mostre que a concentração de sal depois de t minutos (gramas por
litro) é
C(t) =
30t
200+ t
(b) O que acontece com a concentração quando t → ∞
Resolução:
(a)
30
g
l
·25t· l
(5000+25t)l
=
750t
5000+25t
=
30t
200+ t
APOSTILA EXERCÍCIOS DE CÁLCULO 14

17. Limites e Continuidade
(b) lim
t→∞
30t
200
=
30 t
(200
t +1) t
= lim
t→∞
30
(200
t +1)
= 30g/l
onde t é o tempo.
20. Encontre as assíntonas horizontal e vertical e esboce o gráfico da seguinte
função:
(a) f (x) =
x2
x2 −1
=
x2
(x +1)(x −1)
Resolução:
Tire o limite da função f (x) tendendo as raízes para encontrar as assín-
tonas verticais :
lim
x→−1
x2
x2 −1
=
x2
(x +1)(x −1)
= lim
x→−1
1
1− 1
x2
= ∞
lim
x→−1
x2
x2 −1
= lim
x→−1
1
1− 1
x2
= ∞
Tire o limite da função f (x) tendendo a infinito para encontrar as assín-
tonas horizontais:
lim
x→∞
x2
x2 −1
= lim
x→∞
1
1− 1
x2
= 1
APOSTILA EXERCÍCIOS DE CÁLCULO 15

18. Limites e Continuidade
Figura 1.6: Gráfico da função f (x).
21. Investigue a continuidade da função seguinte:
(a) f (x) =
x
|x|
, x = 0
−1,x = 0
Resolução:
|x| =
x,x ≥ 0
−x,x < 0
lim
x→0
x
|x|
lim
x→0+
x
x
= 1
lim
x→0−
x
−x
= −1
A função é descontínua, pois os limites laterais são diferentes.
22. O potencial φ de uma distribuição de carga num ponto do eixo dos x é
APOSTILA EXERCÍCIOS DE CÁLCULO 16

19. Limites e Continuidade
dado por:
φ(x) =



2πσ x2 + a2 − x , se x ≥ 0
2πσ x2 + a2 + x , se x < 0
com a > 0 e σ > 0. φ é contínua em 0? Justifique.
Resolução:
lim
x→0+
2πσ( x2 + a2 − x) = 2πσa
lim
x→0+
2πσ( x2 + a2 + x) = 2πσa
Como os limites laterais são iguais a função é contínua em 0;
23. Dizemos que uma função f é contínua em um ponto a se, e somente se,
lim
h→0
f (a +h) = f (a)
Use esse fato para demonstrar que as funções sen (x) e cos(x) são contí-
nuas.
Resolução:
lim
x→0
sen (x + a) = sen a
24. Calcule:
(a) lim
x→0
sen 3x
x
Resolução:
lim
x→0
3 sen 3x
3x
u = 3x
lim
u→0
3 sen u
u
= 3
25. Calcular o valor de lim
x→0
tanx + x
x
lim
x→0
sen x
cosx
+ x
x
= lim
x→0
sen x
x cosx
+1
APOSTILA EXERCÍCIOS DE CÁLCULO 17

20. Limites e Continuidade
lim
x→0
sen x
x
· lim
x→0
1
cosx
+1
lim
x→0
tanx + x
x
= 2
26. Determine: lim
x→0
1−cos2
x
1−cosx
Resolução:
lim
x→0
1−cos2
x
1−cosx
·
1+cosx
1+cosx
lim
x→0
(1−cos2
x)(1+cosx)
(1−cos2 x)
lim
x→0
1+cosx = 2
27. Sabendo que lim
x→0
sen x
x
= 1, calcule lim
x→π
4
cosx − sen x
cos2x
Resolução:
cos2x = cos(x + x) = cosx cosx − sen x sen x
cos2x = cos2
x − sen 2
x
lim
x→π
4
cosx − sen x
cos2 x − sen 2x
= lim
x→π
4
cosx − sen x
(cosx − sen x)(cosx + sen x)
lim
x→π
4
1
cosx + sen x
=
2
2
28. Calcule os limites:
(a) lim
x→0
sen 3x
2x
(b) lim
x→0
1−cosx
x
(c) lim
x→0
1+ sen x − 1− sen x
x
Resolução:
(a) lim
x→0
sen 3x
2x
APOSTILA EXERCÍCIOS DE CÁLCULO 18

21. Limites e Continuidade
u = 3x x =
u
3
lim
u→0
sen u
2u
3
3
2
lim
u→0
sen u
u
=
3
2
(b) lim
x→0
1−cosx
x
lim
x→0
1−cosx
x
·
1+cosx
1+cosx
= lim
x→0
1−cos2
x
x(1+cosx)
sen 2
x +cos2
x = 1 ⇒ sen 2
x = 1−cos2
x
lim
x→0
sen x
x
· lim
x→0
sen x · lim
x→0
1
1+cosx
= 1·0·
1
2
= 0
(c) lim
x→0
1+ sen x − 1− sen x
x
lim
x→0
1+ sen x − 1− sen x
x
·
1+ sen x + 1− sen x
1+ sen x + 1− sen x
lim
x→0
1+ sen x −(1− sen x)
x( 1+ sen x + 1− sen x)
lim
x→0
2 sen x
x( 1+ sen x + 1− sen x)
2· lim
x→0
sen x
x
· lim
x→0
1
x( 1+ sen x + 1− sen x)
= 2·1·
1
2
= 1
29. Calcule os limites:
(a) lim
x→∞
1−
3
x
x
(b) lim
x→∞
1−
4
x
5x
(c) lim
x→∞
x +1
x −1
x
(d) lim
x→∞
x +5
x
2x+3
Resolução:
APOSTILA EXERCÍCIOS DE CÁLCULO 19

22. Limites e Continuidade
(a) lim
x→∞
1−
3
x
x
Limite fundamental: lim
x→∞
1+
1
x
x
= e
1−
3
x
= 1+
1
y
⇒
−3
x
=
1
y
x = −3y
lim
y→∞
1+
1
y
−3y
= lim
y→∞
1+
1
y
y −3
lim
x→∞
1−
3
x
x
=
1
e3
(b) lim
x→∞
1−
4
x
5x
1−
4
x
= 1+
1
y
⇒
−4
x
=
1
y
x = −4y
lim
x→∞
1−
4
−4y
−20y
= lim
y→∞
1+
1
y
y −20
= e−20
(c) lim
x→∞
x +1
x −1
x
x +1
x −1
= 1+
1
y
x +1 = x −1+
x −1
y
2y = x −1
x = 2y +1
2y+ 2
2y
2y+1
=
y +1
y
2y+1
= 1+
1
y
2y
· 1+
1
y
APOSTILA EXERCÍCIOS DE CÁLCULO 20

23. Limites e Continuidade
lim
y→∞
1+
1
y
y 2
· lim
y→∞
1+
1
y
y
= e2
(d) lim
x→∞
x +5
x
2x+3
x +5
x
= 1+
1
y
x +5 = x +
x
y
5y = x
5y+ 5
5y
10y+3
= 1+
1
y
10y+3
lim
x→∞
1+
1
y
10y+3
= lim
x→∞
1+
1
y
y 10
· lim
x→∞
1+
1
y
3
= e10
APOSTILA EXERCÍCIOS DE CÁLCULO 21

24. CAPÍTULO 2
DERIVADAS
1. Ache uma equação da reta tangente à curva y = 2x2
+ 3 que é paralela à
reta 8x − y +3 = 0.
Resolução:
8x − y +3 = 0
y = 8x +3
y = 2x2
+3
y = 4x = 8
x = 2
y(2) = 11
y −11 = 8(x −2)
y −11 = 8x −16
y = 8x −5
2. Usando a definição, determine a função primeira derivada e as derivadas
nos pontos indicados:
f (x) = x2
−1, f (0) e f (1)
22

25. Derivadas
Resolução:
lim
h→0
(h + x)2
−1− x2
+1
h
= lim
h→0
h2
+2 hx+ x2
− 1− x2
+ 1
h
= lim
h→0
h +2x = 2x
f (0) = 0 ; f (1) = 2
3. Se uma bola for atirada ao ar com uma velocidade de 10m/s, a sua altura
(em metros) deposis de t segundos é dada por y = 10t −4,9t2
. Encontre
a velocidade quando t = 2.
Resolução:
y(t) = 10t −4.9t2
v(t) = y (t)
v(t) = lim
h→0
10(h + t)−4,9(h + t)2
−10t +4,9t2
h
v(t) = lim
h→0
10h +10t −4,9(h2
+2ht + t2
)−10t +4,9t2
h
v(t) = lim
h→0
h(10−4,9h −9,8t)
h
= 10−9,8t
v(2) = −9,6m/s
4. Determine se existir ou não f (0).
f (x) =



x2
sen
1
x
, se x = 0
0 , se x = 0
Resolução:
f (0) = lim
x→0
f (x)− f (0)
x −0
= lim
x→0
x sen (1/x) = 0
Logo o limite existe.
5. Seja f (x) = 3
x.
(a) Se a = 0, usando a definição de derivada no ponto, encontre f (a).
(b) Mostre que f (0) não existe.
(c) Mostre que y = 3
x tem uma reta tangente vertical em (0,0).
APOSTILA EXERCÍCIOS DE CÁLCULO 23

26. Derivadas
Resolução:
(a)
f (a) = lim
h→0
f (a +h)− f (a)
h
= lim
h→0
3
(a +h)− 3
a
h
= lim
h→0
3
(a +h)− 3
a
h
·
3
(a +h)2 + 3
(a +h)a +
3
a2
3
(a +h)2 + 3
(a +h)a +
3
a2
= lim
h→0
3
(a +h)3 −
3
a3
h(
3
(a +h)2 + 3
(a +h)a +
3
a2)
= lim
h→0
a+ h− a
h(
3
(a +h)2 + 3
(a +h)a +
3
a2)
= lim
h→0
1
3
(a +h)2 + 3
(a +h)a +
3
a2
= lim
h→0
1
3
a2 +
3
a2 +
3
a2
=
1
3
3
a2
(b) f (0) = 1/0, que é indeterminação.
(c) A função é contínua em x = 0 e a f (0) = +∞. Por isso, existe a reta
tangente vertical nesse ponto.
6. Mostre que a função f (x) = |x−6| não é diferenciavel em 6. Encontre uma
fórmula para f e esboce seu gráfico.
Resolução:
Lembre-se:
|x| =
x , x > 0
−x , x < 0
APOSTILA EXERCÍCIOS DE CÁLCULO 24

27. Derivadas
Para x > 6
f (a) = lim
h→0
h+ a− 6− a+ 6
h
= 1
Para x < 6
f (a) = lim
h→0
−h− a+ 6+ a− 6
h
= −1
Os limites laterais são diferentes, logo não existe derivada no ponto 6.
f (x) =
−1 , x < 6
1 , x > 6
Figura 2.1: Gráfico da função f (x).
7. Em que ponto da curva y = x2
+8 a inclinação da tangente é 16? Escreva
a equação dessa reta tangente.
Resolução:
f (a) = 16 f (x) = x2
+8
lim
h→0
(h + a)2
+8− a2
−8
h
= lim
h→0
h2
+2 ha+ a2
+ 8− a2
− 8
h
= lim
h→0
h +2a = 2a
f (a) = 2a = 16, a = 8, y = 82
+8 = 72
APOSTILA EXERCÍCIOS DE CÁLCULO 25

28. Derivadas
Ponto (8,72)
Encontrando a reta tangente:
y −72 = 16(x −8)
y = 16x −56
8. Se f (x) = 2x2
−x3
, encontre f (x), f (x), f (x) e f (4)
. Trace f , f , f e f
em uma única tela. Os gráficos são consistentes com as interpretações
geométricas destas derivadas?
Resolução:
f (x) = 4x −3x2
f (x) = 4−6x
f (x) = 6
f (4)
= 0
APOSTILA EXERCÍCIOS DE CÁLCULO 26

29. Derivadas
Figura 2.2: Gráfico das funções f (x), f (x), f (x), f (x).
9. Lembre-se de que uma função f [e chamada par se f (−x) = f (x) para
todo x em seu domínio e, ímpar se f (−x) = −f (x) para cada um destes x.
Demonstre cada uma das afirmativas a seguir:
(a) A derivada de uma função par é uma função ímpar.
(b) A derivada de uma função ímpar é uma função par.
Resolução:
(a) Escolhendo a função cos(x) :
lim
h→0
cos(h + x)−cosx
h
lim
h→0
cosh cosx − sen x sen h −cosx
h
APOSTILA EXERCÍCIOS DE CÁLCULO 27

30. Derivadas
lim
h→0
cosx(cosh −1)
h
− lim
h→0
sen x sen h
h
− sen x Uma função ímpar
(b) Escolhendo a função sen (x) :
lim
h→0
sen (h + x)− sen x
h
lim
h→0
sen h cosx + sen x cosh − sen x
h
lim
h→0
cosx
sen h
h
+ lim
h→0
sen x
(cosh −1)
h
cosx uma função par
10. Encontre a derivada de cada uma das funções.
(a)f (x) =
3
2x
+2x(
5
x3)−
2
x
(b)f (x) =
t3
−3t
t5 −5t
(t2
−2t)
(c)f (x) = x2
sen (x)−ln(x)cos(x)
Resolução:
(a) f (x) =
3
2x
+2x(
5
x3)−
2
x
f (x) =
3
2
x−1
+2x · x3/5
−2x−1/2
f (x) =
3
2
x−1
+2x8/5
−2x−1/2
f (x) =
−3
2
x−2
+
16
5
x · x3/5
+ x−3/2
=
−3
2x2
+
16
5
5
x3 +
1
3
x2
(b) f (x) =
t3
−3t
t5 −5t
(t2
−2t)
APOSTILA EXERCÍCIOS DE CÁLCULO 28

31. Derivadas
Utilizando a regra do quociente:
f (t) =
(t5
−5t)(5t4
−8t3
−9t2
+12t)−(t5
−2t4
−3t3
+6t2
)(5t4
−5)
(t5 −5t)2
f (t) =
2t8
+6t7
−18t6
−20t5
+30t4
+30t3
−30t2
(t5 −5t)2
(c) f (x) = x2
sen (x)−ln(x)cos(x)
Utilizando a regra do produto:
f (x) = 2x sen x + x2
cosx −
1
x
cosx +lnx ·− sen x
f (x) = sen x(2x +lnx)+cosx(x2
−1/x)
11. Suponha que a curva y = x4
+ax3
+bx2
+cx +d tenha uma reta tangente
quando x = 0 com equação y = 2x +1 e, uma reta tangente quando x = 1
com equação y = 2−3x. Encontre os valores de a,b,c ed.
Resolução:
f (0) = 2; f (1) = −3
f (x) = 4x3
+3ax2
+2bx +c
f (0) = c = 2
f (1) = 3a +2b = −9
f (0) = d = 1
f (1) = a +b = −5
3a +2b = −9
a +b = −5
a = 1; b = −6
APOSTILA EXERCÍCIOS DE CÁLCULO 29

32. Derivadas
12. Se f (x) = ex
· g(x), em que g(0) = 2 e g (0) = 5. É correto dizer que f (0) é:
(a)7 (b)2 (c)5 (d) 10
Resolução:
f (x) = ex
g(x)+ex
g (x); f (0) = e0
g(0)+e0
g (0)
f (0) = 2+5 = 7
Resposta: letra (a)
13. Encontre um polinômio de segundo grau P tal que P(2) = 5,P (2) = 3 e
P (2) = 2.
Resolução:
P(x) = ax2
+bx +c
P (x) = 2ax +b
P (x) = 2a
P(2) = 4a +2b +c = 5
P (2) = 4a +b = 3
P (2) = 2a = 2
a = 1
4+b = 3 ⇒ b = −1
4−2+c = 5 ⇒ c = 3
14. Encontre as derivadas das funções dadas.
(a)f (x) = (3x5
−1)10
(2− x4
)
(b)f (s) = ln(e5s−3
)
(c)f (θ) = 2cos2
(θ) sen (θ)
(d)f (x) = ln( sen 2
(x))
Resolução:
(a)f (x) = (3x5
−1)10
(2− x4
)
Obs. Utiliza-se a regra da cadeia e a do produto.
10(3x5
−1)9
(15x4
)(2− x4
)+(3x5
−1)10
·−4x3
(b)f (s) = ln(e5s−3
)
5e5s−3
e5s−3
= 5
(c)f (θ) = 2cos2
(θ) sen (θ)
f (θ) = −4cos(θ) sen (θ) sen (θ)+2cos2
(θ)cos(θ)
= −4cos(θ) sen 2
(θ)+2cos3
(θ)
(d)f (x) = ln( sen 2
(x))
APOSTILA EXERCÍCIOS DE CÁLCULO 30

33. Derivadas
1
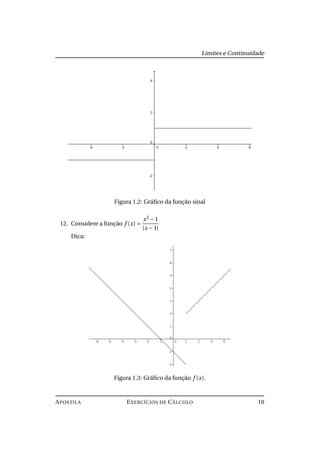
sen 2(x)
·2 sen (x)cos(x) =
2cosx
sen x
= 2cotx
15. Usando a regra da cadeia, determine y , sendo:
(a) y = (3x +5)50
(b) y =
1
(x3 +3x2 −6x +4)
(c) y = sec2
[(x3
−6)3
]
(d) y =
1
x(x +1)
Resolução:
(a) y = (3x +5)50
y = 50(3x +5)49
·3 = 150(3x +5)49
(b) y =
1
x3 +3x2 −6x +4
= (x3
+3x2
−6x +4)−1
y = −(x3
+3x2
−6x +4)−2
·(3x2
+6x −6) =
−(3x3
+6x −6)
(x3 +3x2 −6x +4)2
(c) Derivada tabelada:
d secx
dx
= secx ·tanx
y = sec2
[(x3
−6)3
]
y = 2sec[(x3
−6)3
]·sec[(x3
−6)3
]·tan[(x3
−6)3
]·3(x3
−6)2
·3x2
y = 18x2
sec2
[(x3
−6)3
]tan[(x3
−6)3
](x3
−6)2
(d) y =
1
x(x +1)
= [x(x +1)]−1
y = −[x(x +1)]−2
·[(x +1)+ x]
=
−(2x +1)
[x(x +1)]2
16. Seja f uma função derivável e g(x) = ex
f (3x +1). Cacule g (0) se f (1) = 2
e f (1) = 3.
g(x) = ex
f (3x +1)
g (x) = ex
f (3x +1)+ex
f (3x +1)·3
g (0) = e0
f (1)+e0
f (1)·3 = 2+9 = 11
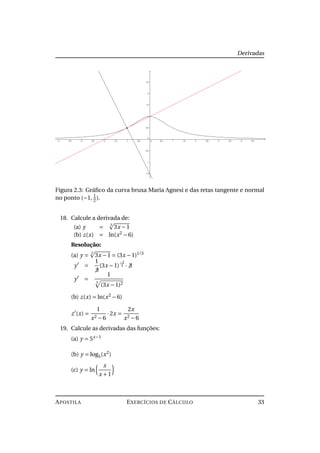
17. A curva y = 1/(1+ x2
) é chamada bruxa de Maria Agnesi.
(a) Encontre uma equação da reta tangente e uma equação da reta norma
para essa curva no ponto (−1, 1
2).
(b)Ilustre a parte (a) fazendo o gráfico da curva e das retas tangentes e
normal no mesmo plano.
APOSTILA EXERCÍCIOS DE CÁLCULO 31

34. Derivadas
Resolução:
y = (1+ x2
)−1
y = −(1+ x2
)−2·2x =
−2x
(1+ x2)2
Encontrando a reta tangente no ponto (−1, 1
2)
f (−1) =
−2·−1
(1+(−1)2)2
=
1
2
y − 1
2 = 1
2(x −(−1))
y − 1
2
= 1
2
x + 1
2
y = 1
2
x +1
Encontrando a reta normal no ponto (−1, 1
2
)
y −
1
2
=
−1
f (−1)
(x +1)
y −
1
2
= −2(x +1)
y −
1
2
= −2x −2
y = −2x −
3
2
APOSTILA EXERCÍCIOS DE CÁLCULO 32

35. Derivadas
Figura 2.3: Gráfico da curva bruxa Maria Agnesi e das retas tangente e normal
no ponto (−1, 1
2).
18. Calcule a derivada de:
(a) y =
3
3x −1
(b) z(x) = ln(x2
−6)
Resolução:
(a) y =
3
3x −1 = (3x −1)1/3
y =
1
3
(3x −1)
−2
3 · 3
y =
1
3
(3x −1)2
(b) z(x) = ln(x2
−6)
z (x) =
1
x2 −6
·2x =
2x
x2 −6
19. Calcule as derivadas das funções:
(a) y = 5x−1
(b) y = log5(x2
)
(c) y = ln
x
x +1
APOSTILA EXERCÍCIOS DE CÁLCULO 33

36. Derivadas
Resolução:
Dica:
d(loga x)
dx
=
1
x lna
(a) y = 5(x−1)
ln y = ln5(x−1)
ln y = (x −1)ln5
1
y
· y = ln5
y = y ln5
y = 5(x−1)
·ln5
(b) y = log5(x2
)
y =
1
x2 ln5
·2x =
2
x ln5
(c) y = ln
x
x +1
= lnx −ln(x +1)
y =
1
x
−
1
x +1
=
1
x2 + x
20. Calcule y se:
(a)y = 1−tan2(x)
(b)y = x cot(2x)
(c)y = tan(sec(x2
))
Resolução:
Derivadas tabeladas:
d(tanx)
dx
= sec2
x;
d(secx)
dx
= secx ·tanx
(a)y = 1−tan2(x) = (1−tan2
x)
1
2
APOSTILA EXERCÍCIOS DE CÁLCULO 34

37. Derivadas
y = −
1
2
(1−tan2
x)−1
2 ·[ 2tanx ·sec2
x]
y =
−tanx ·sec2
x
1−tan2 x
(b)y = x cot(2x)
y = cot(2x)−2cossec2
(2x)
(c)y = tan(sec(x2
))
y = sec2
[sec(x2
)]·sec(x2
)·tan(x2
)·2x
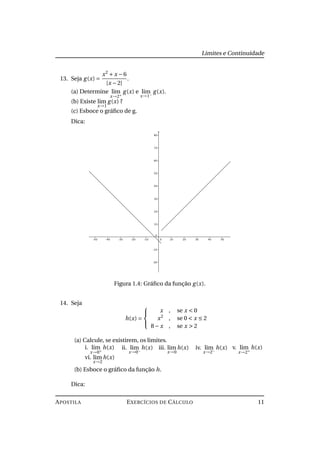
21. Encontre:
d99
dx99
( sen x)
Resolução:
d
dx
sen x = cosx
d2
dx2
sen x = − sen x
d3
dx3
sen x = −cosx
d4
dx4
sen x = sen x
d5
dx5
sen x = cosx
99 4
3 24
d99
dx99
( sen x) =
d3
dx3
( sen x)
= −cosx
22. Encontre constantes A e B de forma que a função y = A sen x + B cosx
satisfaça a equação diferencial y + y −2y = sen x.
Resolução:
APOSTILA EXERCÍCIOS DE CÁLCULO 35

38. Derivadas
y = Acosx −B sen x
y = −A sen x −B cosx
−A sen x −B cosx + Acosx −B sen x −2A sen x −2B cosx = sen x
(−3A −B) sen x +(A −3B)cosx = 1 sen x +0cosx
−3A −B = 1
A −3B = 0
A =
−3
10
; B =
−1
10
23. Ache
∂y
∂x
por derivação implicita de x2
+ y2
= 16
Resolução:
2x +2y · y = 0
2y · y = −2x
y =
− 2x
2y
y =
−x
y
24. Ache uma equação da reta tangente à curva 16x4
+y4
= 32 no ponto (1,2).
Resolução:
Derivando a curva:
64x3
+4y3
· y = 0
4y3
y = −64x3
y =
−64x3
4y3
= −
16x3
y3
y (1,2) = −2
Equação da reta tangente:
y −2 = −2(x −1)
y −2 = −2x +2
y = −2x +4
APOSTILA EXERCÍCIOS DE CÁLCULO 36

39. Derivadas
25. Ache uma equação da reta normal à curva x2
+xy +y2
−3y = 10 no ponto
(2,3).
Resolução:
2x + y + xy +2yy −3y = 0
(x +2y −3)y = −2x − y
y =
−2x − y
x +2y −3
y (2,3) =
−7
5
Equação da reta normal:
t − t0 = −
1
y
(x − x0)
t −3 =
5
7
(x −2)
t −3 =
5
7
x −
10
7
t =
−5
7
x
−11
7
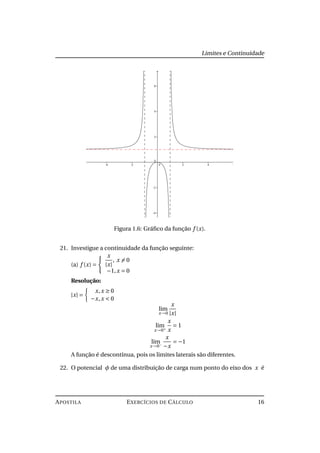
26. Use a derivação logarítmica para encontrar as derivadas das seguintes
funções:
(a) y = (2x +1)5
(x4
−3)6
(b) y =
x −1
x4 +1
(c) y = xx
(d) y = xcosx
Resolução:
(a)y = (2x +1)5
(x4
−3)6
ln y = ln[(2x +1)5
(x4
−3)6
]
ln y = ln(2x +1)5
+ln(x4
−3)6
ln y = 5ln(2x +1)+6ln(x4
−3)
1
y
· y =
10
2x +1
+
24x3
x4 −3
y = [(2x +1)5
(x4
−3)6
]·
10
2x +1
+
24x3
x4 −3
APOSTILA EXERCÍCIOS DE CÁLCULO 37

40. Derivadas
(b)y =
x −1
x4 +1
ln y = ln
x −1
x4 +1
1/2
=
1
2
ln
x −1
x4 +1
=
1
2
ln(x −1)−ln(x4
+1)
1
y
· y =
1
2(x −1)
−
4x3
2(x4 +1)
y =
x −1
x4 +1
·
1
2(x −1)
−
4x3
2(x4 +1)
(c)y = xx
y = xx
ln y = lnxx
ln y = x lnx
1
y
· y = lnx + x ·
1
x
y = y ·[lnx +1]
y = xx
·[lnx +1]
(d)y = xcosx
ln y = ln(xcosx
)
ln y = cosx ·lnx
1
y
· y = − sen x ·lnx +
cosx
x
y = xcosx cosx
x
− sen x ·lnx
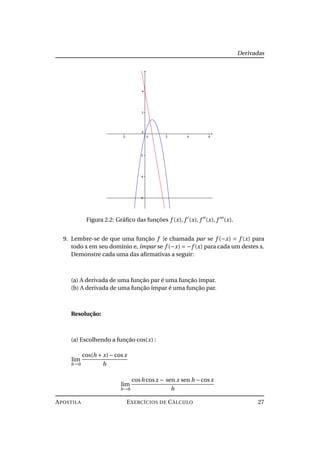
27. Seja f (x) = a +b cos(2x)+c cos(4x), onde a,b,c ∈ R. Sabendo que f ( π
2)
=
1, f (0) = f (0) = f (0) = f (3)
(0) = 0 e que f pode ser escrita na forma
f (x) = sen n
(x),n ∈ N, determine a,b,c en.
Resolução:
APOSTILA EXERCÍCIOS DE CÁLCULO 38

41. Derivadas
f (x) = a +b cos(2x)+c cos(4x)
f (x) = −b2 sen (2x)−4c sen (4x)
f (x) = −4b cos(2x)−16c cos(4x)
f (3)
(x) = 8b sen (2x)+64c sen (4x)
f (0) = −4b −16c = 0
f (0) = a +b = c = 0
f (π/2) = a −b +c = 1
Resolvendo o sistema acima:
a =
3
8
; b =
−1
2
; c =
1
8
f (x) =
3
8
−
1
2
cos(2x)+
1
8
cos(4x)
=
3
8
−
1
2
(cos2
x − sen 2
x)+
1
8
cos(4x)
=
3
8
−
4
8
(1−2 sen 2
x)+
1
8
cos(4x)
= −
1
8
+ sen 2
x +
1
8
cos(4x)
1
8
cos4x =
1
8
[cos(2x)cos(2x)− sen (2x) sen (2x)]
=
1
8
[cos2
(2x)− sen 2
(2x)]
=
1
8
(1−2 sen 2
(2x))
f (x) = −
1
8
+ sen 2
(x)+
1
8
−
2
8
sen 2
(2x)
= sen 2
x −
2
8
sen 2
(2x)
sen 2
(2x) = ( sen x cosx + sen x cosx)2
= (2 sen x cosx)2
= 4 sen 2
x cos2
x
APOSTILA EXERCÍCIOS DE CÁLCULO 39

42. Derivadas
f (x) = sen 2
x −
2
8
(4 sen 2
x cos2
x)
= sen 2
x − sen 2
x cos2
x
= sen 2
x(− 1+ 1+ sen 2
x)
= sen 2
x · sen 2
x = sen 4
x
n = 4
28. Determine a equação da reta tangente e da reta normal à curva y = arcsin
x −1
2
no ponto onde a curva intersecta o eixo dos x.
Resolução:
Valor tabelado :
d
dx
arcsinx =
1
1− x2
Encontrando o ponto onde a curva intersecta o eixo dos x:
arcsin
x −1
2
= 0
x −1
2
= 0 ⇒ x = 1
Ponto : (1,0)
y =
1
1−
x −1
2
2
·
1
2
y =
1
2
Reta tangente:
y −0 =
1
2
(x −1)
y =
1
2
x −
1
2
Reta normal:
y −0 = −
1
1/2
(x −1)
APOSTILA EXERCÍCIOS DE CÁLCULO 40

43. Derivadas
y = −2(x −1)
y = −2x +2
APOSTILA EXERCÍCIOS DE CÁLCULO 41

44. REFERÊNCIAS BIBLIOGRÁFICAS
[1] LEITHOLD, L. O Cálculo com Geometria Analítica. Vol. 1. 3 ed. São Paulo:
Harbra, 1994.
[2] STEWART, J. Cálculo. Vol. 1. 6 ed. São Paulo: Cengage Learning, 2011.
[3] GUIDORIZZI, H. Um Curso de Cálculo. Vol. 1. 5 ed. Rio de Janeiro: LTC,
2012.
42