1) O documento apresenta conceitos matemáticos como conjuntos numéricos, potenciação, radiciação e equações do 2o grau.
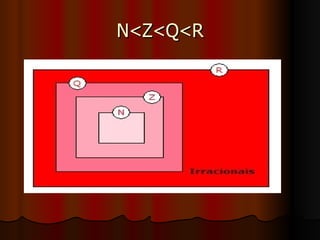
2) Inclui definições de conjuntos como N, Z, Q, R e suas propriedades.
3) Explica a operação de potenciação, suas propriedades e como resolver equações do 2o grau usando a fórmula de Bhaskara.





































![DEDUÇÃO: x² + (b/a) x + (b/2a)² = -c/a + (b/2a)² Simplificando ambos os lados da equação, obteremos: [x+(b/2a)] 2 = (b² - 4ac) / 4a²](https://image.slidesharecdn.com/conjuntoeequaodo2grau-090502141603-phpapp02/85/Conjunto-E-EquacaO-Do-2-Grau-39-320.jpg)
![OBSERVE: Extraindo a raiz quadrada de cada membro da equação e lembrando que a raiz quadrada de todo número real não negativo é também não negativa, obteremos duas respostas para a nossa equação: x + (b/2a) = + R[(b²-4ac) / 4a²] ou x + (b/2a) = - R[(b²-4ac) / 4a²]](https://image.slidesharecdn.com/conjuntoeequaodo2grau-090502141603-phpapp02/85/Conjunto-E-EquacaO-Do-2-Grau-40-320.jpg)

![x² - 5 x + 6 = 0 Identificar os coeficientes: a=1, b= -5, c=6 Escrever o discriminante D = b²-4ac. Calcular D=(-5)²-4×1×6=25-24=1 Escrever a fórmula de Bhaskara: Substituir os valores dos coeficientes a, b e c na fórmula: x' = (1/2)(5+R[1]) = (5+1)/2 = 3 x" = (1/2)(5-R[1]) = (5-1)/2 = 2](https://image.slidesharecdn.com/conjuntoeequaodo2grau-090502141603-phpapp02/85/Conjunto-E-EquacaO-Do-2-Grau-42-320.jpg)











