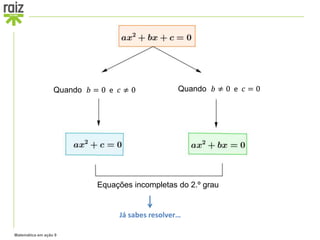
O documento discute equações de 1o e 2o grau. Explica como reduzir equações a forma ax = b para equações de 1o grau e como resolver equações de 2o grau completas e incompletas usando fórmulas como a fórmula resolvente. Inclui exemplos passo a passo de como resolver diferentes tipos de equações.

1. Matemática em ação 9
Equações
Equações do 1.º grau e do 2.º grau

2. Matemática em ação 9
Atividade Equações do 1.º grau
Observa as equações:
a) Reduz cada uma delas à forma 𝑎𝑥 = 𝑏 , em que 𝑎 e 𝑏
representam números reais.
b) Acaba de as resolver.
1
Toda a equação que se pode reduzir a uma equação do tipo
𝑎𝑥 = 𝑏, em que 𝑎 e 𝑏 representam números reais, diz-se uma
equação do 1.º grau.
Porquê do 1.º grau? Repara que o 1.º membro é um polinómio
(monómio) de grau 1.
−2𝑥 + 24 = 0
𝑥 − −9 + 5𝑥 = 10 − 𝑥
1 −
𝑥 + 2
6
=
𝑥
8
Soluções

3. Matemática em ação 9
Uma equação que se pode reduzir à forma
𝑎𝑥2
+ 𝑏𝑥 + 𝑐
polinómio do 2º grau
= 0 , 𝑎 ≠ 0 ,
em que o primeiro membro é um polinómio do 2.º grau, diz-se uma
equação do 2.º grau .
Chama-se equação do 2.º grau a toda a equação que se
pode reduzir à forma
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0 ,
em que 𝑎, 𝑏 e 𝑐 representam números reais e 𝑎 ≠ 0
Equações do 2.º grau

4. Matemática em ação 9
Já sabes resolver…
Quando 𝑏 = 0 e 𝑐 ≠ 0 Quando 𝑏 ≠ 0 e 𝑐 = 0
Equações incompletas do 2.º grau

5. Matemática em ação 9
Atividade Equações incompletas do 2.º grau
2
2.1. Equações incompletas do tipo 𝒂𝒙𝟐+𝒄 = 𝟎
Resolve as equações:
a) 9𝑥2
− 7 = 0 b) 𝑥2
+ 36 = 0 c) 5𝑥2
= 200
2.2. Equações incompletas do tipo 𝒂𝒙𝟐+𝒃𝒙 = 𝟎
Resolve as equações:
a) 2𝑥2 + 3𝑥 = 0 b) −𝑥2 + 14𝑥 = 0 c) 5𝑥2
= 2𝑥
2.3. Quando 𝒃 = 0 e 𝒄 = 0 : equações incompletas do tipo 𝒂𝒙𝟐= 𝟎
Resolve a equação 23𝑥2
= 0 .
Soluções

6. Matemática em ação 9
Atividade Equações completas do 2º grau
3
Como a resolver?
Obtiveste uma equação completa do 2.º grau.
a) Escreve-a na forma 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0 e indica o valor de 𝑎 , de 𝑏
e de 𝑐 .
Considera a equação 2𝑥 𝑥 +
5
2
= 3 .
R: 𝟐𝒙𝟐
+ 𝟓𝒙 − 𝟑 = 𝟎 , com 𝒂 = 𝟎 , 𝒃 = 𝟓 e 𝒄 = −𝟑

7. Matemática em ação 9
Atividade Equações completas do 2º grau
3
Com 𝑎 ≠ 0 ,
b) Aplica a fórmula resolvente para resolveres a equação dada.
Demonstra-se que qualquer equação do 2.º grau se pode
resolver utilizando a fórmula seguinte:
𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0 𝑥 =
−𝑏 ± 𝑏2 − 4𝑎𝑐
2𝑎
fórmula resolvente
R: 𝑺 = −𝟑,
𝟏
𝟐

8. Matemática em ação 9
Atividade Equações completas do 2.º grau
4
Considera as equações completas do 2.º grau:
I) 𝑥2
+ 10𝑥 + 25 = 0 II) 4𝑥2
− 12𝑥 + 9 = 0
4.1. Nas duas equações, o 1.º membro é o desenvolvimento do quadrado
de um binómio.
Identifica em cada caso o quadrado do binómio e resolve as equações
pela lei do anulamento do produto.
4.2. Resolve as duas equações utilizando a fórmula resolvente.
R: I) (𝑥 + 5)2
= 0 ; 𝑆 = −5 solução dupla II) (2𝑥 − 3)2
= 0; 𝑆 =
3
2
solução dupla
Qual o processo que te pareceu mais simples?

9. Matemática em ação 9
Atividade Equações do 2º grau
5
Resolve as seguintes equações da atividade 2, utilizando a
fórmula resolvente:
Qual o processo que te pareceu mais simples?
Caso não te proponham um caminho,
resolve as equações do 2.º grau pelo
método que te parecer mais
conveniente.
2.1. a) 9𝑥2
− 7 = 0 2.2. b) −𝑥2
+ 14𝑥 = 0

10. Matemática em ação 9
1. a)
b)
voltar
−2𝑥 = −24 em que 𝑎 = −2 e 𝑏 = −24
−3𝑥 = 1 em que 𝑎 = −3 e 𝑏 = 1
−𝑥 = −16 em que 𝑎 = −1 e 𝑏 = −16
Soluções:
𝑆 = 12
𝑆 = −
1
3
𝑆 = 16

11. Matemática em ação 9
2.
2.1. a) 𝑆 = −
𝟕
𝟑
,
𝟕
𝟑
b) Equação impossível. 𝑆 =
c) 𝑆 = −2 10, 2 10
2.2.a) 𝑆 = −
3
2
, 0
b) 𝑆 = 0, 14
c) 𝑆 = 0,
2
5
2.3. 𝑆 = 0
Soluções:
voltar