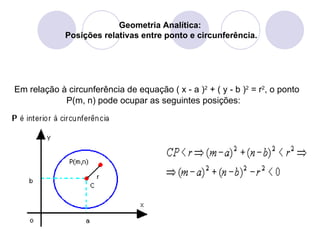
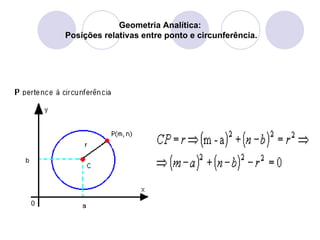
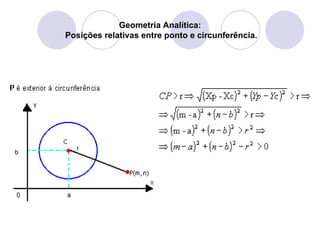
O documento discute as posições relativas de um ponto em relação a uma circunferência em geometria analítica, identificando três possibilidades: ponto interno, ponto pertencente ou externo. Exemplos resolvidos ilustram como calcular a distância entre o ponto e o centro da circunferência para determinar sua posição.

1. Geometria Analítica: Posições relativas entre ponto e circunferência. A aula a seguir traz demonstrações e alguns exercícios resolvidos de posições que um determinado ponto pode assumir em relação a uma circunferência. Dispomos de três possibilidades: 1ª Ponto interno em relação a circunferência. 2ª Ponto pertencente a circunferência. 3ª Ponto externo à circunferência

2. Geometria Analítica: Posições relativas entre ponto e circunferência. Lembre-se:

3. Geometria Analítica: Posições relativas entre ponto e circunferência. Em relação à circunferência de equação ( x - a ) 2 + ( y - b ) 2 = r 2 , o ponto P(m, n) pode ocupar as seguintes posições:

4. Geometria Analítica: Posições relativas entre ponto e circunferência.

5. Geometria Analítica: Posições relativas entre ponto e circunferência.

6. Geometria Analítica: Posições relativas entre ponto e circunferência. Exercício-1: Qual a posição relativa do ponto P (3, 2) em relação à circunferência de equação Então o ponto P(3, 2) pertence a circunferência uma vez que a distância do centro ao ponto P é igual ao raio. Substituindo:

7. Geometria Analítica: Posições relativas entre ponto e circunferência. Exercício-2: Qual a posição relativa do ponto P (-2, -3) em relação à circunferência de equação Como a distância do centro ao ponto P em questão é menor que zero podemos concluir que o ponto é interno a circunferência. Substituindo:

8. Geometria Analítica: Posições relativas entre ponto e circunferência. Exercício-3: Qual a posição relativa do ponto P (1, 4) em relação à circunferência de equação Substituindo: Nesse caso a distância do ponto ao centro é maior que o raio concluímos então que o ponto é externo à circunferência

9. Geometria Analítica: Posições relativas entre ponto e circunferência. Resumo final: Quando temos um ponto P (m, n) e uma circunferência  , de centro C (a, b) e raio r , podemos afirmar que: P   P é interno a  P é externo a 

10. Geometria Analítica: Posições relativas entre ponto e circunferência. http://ensinodematemtica.blogspot.com Professor: Antonio Carlos Barroso