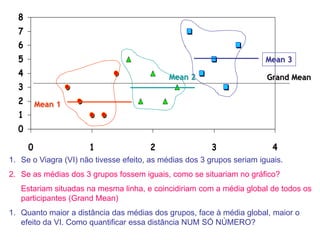
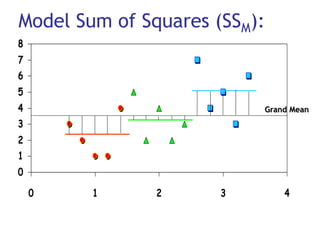
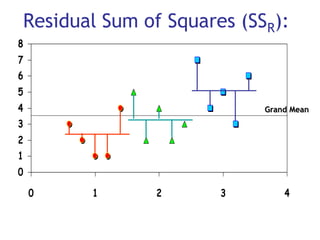
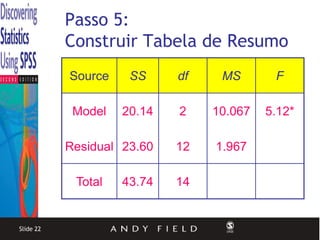
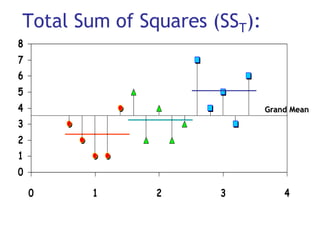
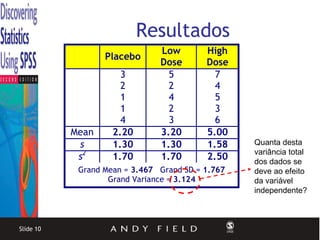
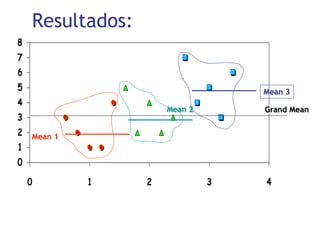
1) O documento apresenta os princípios básicos da análise de variância (ANOVA) em um fator, incluindo quando e por que usar ANOVA em vez de teste t. 2) A ANOVA testa se existe diferença entre as médias de grupos e quantifica a variância entre e dentro dos grupos através das somas dos quadrados do modelo e residual. 3) É apresentado um exemplo ilustrando o cálculo da ANOVA para dados de um estudo sobre os efeitos do Viagra na líbido.

1. One-Way Independent
ANOVA (GLM 1)
Profª Doutora Célia Sales
(Aula com base nos Slides de Andy Field, 2005)
Slide 1

2. Conteúdos
• Princípios básicos da ANOVA:
– Porque se faz?
– O que nos diz?
• Lógica da Anova a 1 factor para
grupos independentes.
Slide 2

3. Quando e Porquê
• Quando queremos comparar médias
usamos um t-test. Este teste tem
limitações:
– Apenas se podem comparar 2 médias:
Frequentemente queremos comparar 3 ou
mais médias.
– Pode apenas usar-se com uma variável
independente(factor ou preditor).
• ANOVA é uma extensão do t-test.
– Compara várias médias.
– Permite manipular várias variáveis
independentes (análise de V. a mais de um
factor – não abordaremos)
Slide 3

4. Porque não usar vários t-Tests?
• Se queremos comparar várias
médias, porque não comparamos
pares de médias com o t-tests?
– Inflacciona o erro de Tipo I
(considerar que existe diferença
quando, na realidade não existe).
– Não permite examinar o efeito de
várias variáveis independentes.
Slide 4

5. O que significa?
ANOVA
Analysis of Variance
Slide 5

6. O que nos diz a ANOVA?
• Hipótese Nula:
– Tal como no t-test, a ANOVA testa a hipótese nula
de que as médias são iguais.
• Hipótese Alternativa:
– As médias são diferentes.
• ANOVA:
– Testa se existe uma diferença entre os grupos, em
geral.
– Diz-nos se as médias dos grupos são diferentes.
– Não nos diz QUAIS as médias que são diferentes.
Slide 6

7. Exemplo - Desenho experimental
• Efeitos do Viagra na líbido, usando
três grupos:
– Placebo (comprimido de açucar)
– Dose Baixa de Viagra
– Dose Alta de Viagra
• Outcome/Variável Dependente (DV)
é uma medida objectiva quantitativa
da líbido.
Slide 7

8. Lógica da ANOVA
O total de variância na Líbido (VD) é
constituída por dois elementos:
Variância devida ao efeito Variância devida a outros
da variável independente factores
(variância explicada pelo (Variância residual ou erro,
modelo em análise) “resto”, isto é, variância não
explicada)
Slide 8

9. Lógica da ANOVA
SST
Variância Total nos Dados
SSM SSR
Efeito devido à VI (devido ao Modelo)
Erro (v. não explic)
• Se o Viagra tiver efeito sobre a
líbido, o modelo vai explicar mais
variância
Slide 9

10. Resultados
Low High
Placebo
Dose Dose
3 5 7
2 2 4
1 4 5
1 2 3
4 3 6
Mean 2.20 3.20 5.00
s 1.30 1.30 1.58 Quanta desta
variância total
s2 1.70 1.70 2.50 dos dados se
Grand Mean = 3.467 Grand SD = 1.767 deve ao efeito
Grand Variance = 3.124 da variável
independente?
Slide 10

11. Resultados:
8
7
6
5 Mean 3
4
Mean 2 Grand Mean
3
2 Mean 1
1
0
0 1 2 3 4

12. 8
7
6
5 Mean 3
4 Mean 2 Grand Mean
3
2 Mean 1
1
0
0 1 2 3 4
1. Se o Viagra (VI) não tivesse efeito, as médias dos 3 grupos seriam iguais.
2. Se as médias dos 3 grupos fossem iguais, como se situariam no gráfico?
Estariam situadas na mesma linha, e coincidiriam com a média global de todos os
participantes (Grand Mean)
1. Quanto maior a distância das médias dos grupos, face à média global, maior o
efeito da VI. Como quantificar essa distância NUM SÓ NÚMERO?

13. Model Sum of Squares (SSM):
8
7
6
5
4 Grand Mean
3
2
1
0
0 1 2 3 4
Slide 13

14. Passo 1: Calcular SSM
Quantificação da distância da média de cada grupo, em
relação à média global (Variabilidade Between Groups)
Model Sum of Squares (SSM)...
SSM   ni (xi  x grand)2
Dimensão do grupo Média do grupo Média global
Slide 14

15. E como quantificar o “resto”
da variância?
• O efeito do Viagra explica a diferença
(variância) entre os grupos
• Não explica as diferenças (variância)
dentro de cada grupo
Como
Variância não explicada, quantificá-la?
residual ou erro
Slide 15

16. Residual Sum of Squares (SSR):
8
7
6
5
4 Grand Mean
3
2
1
0
0 1 2 3 4
Slide 16

17. Passo 2: Calcular SSR
Quantificação da distância de cada observação, face à
média do seu grupo (Variabilidade Within Groups)
Residual Sum of Squares (SSR)...
SSR  (xi  xi ) 2
Slide 17

18. Variabilidade entre os
grupos
(Model Sum of Squares,
e.i., variabilidade explicada
pelo modelo) Variabilidade dentro do
grupo
Variabilidade Total
(Residual Sum of Squares,
(Total Sum of Squares) i.e., variabilidade não
explicada pelo modelo)
SST  SSM  SSR
43 .74  20 .14  23 .60
43 .74  43 .74
Slide 18

19. Passo3: Calcular as médias
das somas dos quadrados
• Dado que o valor das somas dos
quadrados depende da dimensão das
amostras, é necessário fazer a sua
média (tal como no cálculo do desvio-
padrão)
• Esta “média” usa no denominador os
GRAUS DE LIBERDADE (df) em vez
de n.
(mais adiante veremos como se calculam os df)
Slide 19

20. Passo3: Calcular as médias
das somas dos quadrados
SSM 20.135
M SM    10.067
dfM 2
SSR 23.60
M SR    1.967
dfR 12
Slide 20

21. Passo 4: Calcular F-Ratio
M SM
F
M SR
M SM 10.067
F   5.12
M SR 1.967
Slide 21

22. Passo 5:
Construir Tabela de Resumo
Source SS df MS F
Model 20.14 2 10.067 5.12*
Residual 23.60 12 1.967
Total 43.74 14
Slide 22

23. Graus de Liberdade
Degrees of Freedom (df)
• Degrees of Freedom (df) é o nº de valores que
podem variar livremente.
– Pense numa equipa de Rugby!
• Em geral, o valor de df é o nº de valores que
foram usados para o cálculo MENOS UM.
Slide 23

24. Model Degrees of Freedom
• Quantos valores usámos para calcular o
SSM?
– Usámos as médias dos 3 grupos.
dfM  k  1  3  1  2
Slide 24

25. Residual Degrees of Freedom
• Quantos valores usámos para calcular
SSR?
– Usámos as observações de cada grupo.
dfR  dfgroup1  dfgroup2  dfgroup3
 n1  1  n2  1  n3  1
 5  1  5  1  5  1
 12
Slide 25

26. Total Sum of Squares (SST):
8
7
6
5
4 Grand Mean
3
2
1
0
0 1 2 3 4
Slide 26

27. Calculo da variância total
(SST)
SST  (xi  x grand) 2
Slide 27

28. Degrees of Freedom (df)
dfT  N  1  15  1  14
Slide 28

29. Qual a variabilidade total dos
resultados SST?
A variabilidade total dos resultados é dada pelo somatório da
distância de todos as observações, em relação à média
global
Total Sum of squares (SST)
SST  (xi  x grand)2
(a variância total dos dados é dada por SS / df)
Slide 29