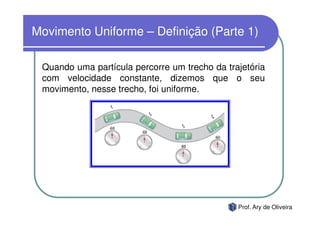
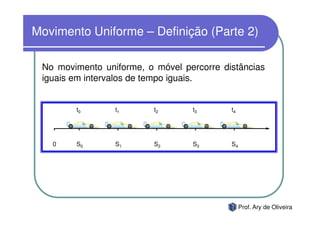
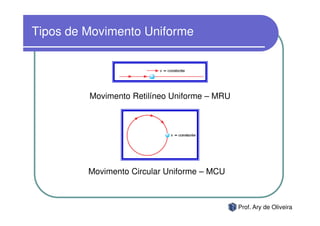
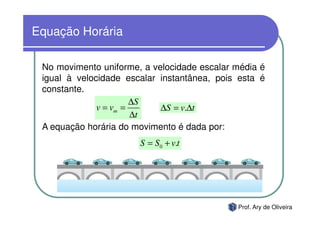
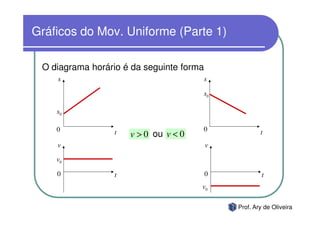
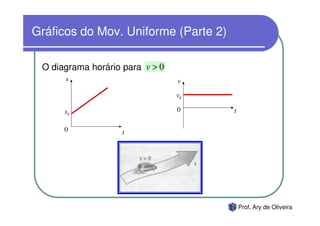
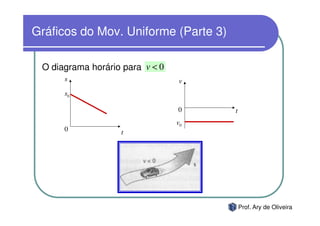
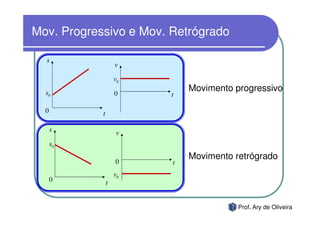
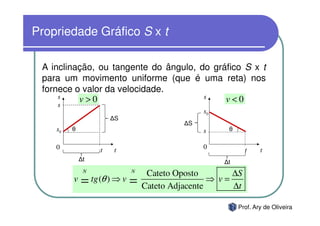
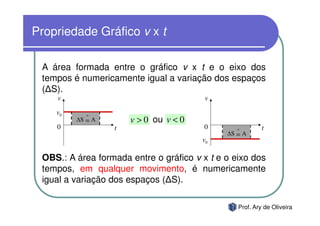
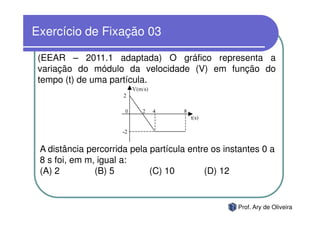
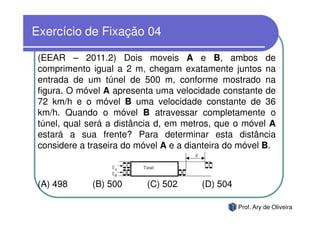
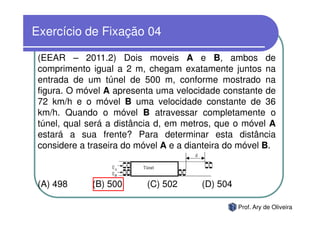
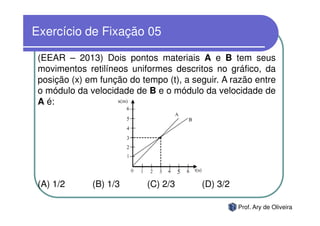
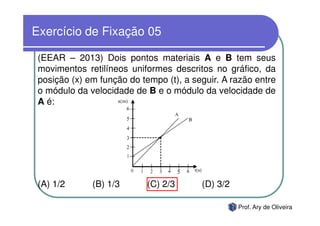
O documento discute o movimento uniforme, definindo-o como quando uma partícula se move com velocidade constante. Apresenta os tipos de movimento uniforme, a equação horária, propriedades dos gráficos de posição versus tempo e velocidade versus tempo, e exercícios sobre o tema.

1. Movimento Uniforme
Movimento Uniforme – Definição; Tipos de Movimento
Uniforme; Equação Horária; Gráficos do Mov. Uniforme;
Mov. Progressivo e Mov. Retrógrado; Propriedade do
Gráfico S x t; Propriedade do Gráfico v x t & Exercícios
de Fixação.
Prof. Ary de Oliveira

2. Movimento Uniforme – Definição (Parte 1)
Quando uma partícula percorre um trecho da trajetória
com velocidade constante, dizemos que o seu
movimento, nesse trecho, foi uniforme.
Prof. Ary de Oliveira

3. Movimento Uniforme – Definição (Parte 2)
No movimento uniforme, o móvel percorre distâncias
iguais em intervalos de tempo iguais.
t0 t1 t2 t3 t4
0 S0 S1 S2 S3 S4
Prof. Ary de Oliveira

4. Tipos de Movimento Uniforme
Movimento Retilíneo Uniforme – MRU
Movimento Circular Uniforme – MCU
Prof. Ary de Oliveira

5. Equação Horária
No movimento uniforme, a velocidade escalar média é
igual à velocidade escalar instantânea, pois esta é
constante.
∆S
v = vm = ∆S = v.∆t
∆t
A equação horária do movimento é dada por:
S = S0 + v.t
Prof. Ary de Oliveira

6. Gráficos do Mov. Uniforme (Parte 1)
O diagrama horário é da seguinte forma
s s
s0
s0
0 t 0 t
v > 0 ou v < 0
v v
v0
0 t 0 t
v0
Prof. Ary de Oliveira

7. Gráficos do Mov. Uniforme (Parte 2)
O diagrama horário para v > 0
s v
v0
s0 0 t
0 t
Prof. Ary de Oliveira

8. Gráficos do Mov. Uniforme (Parte 3)
O diagrama horário para v < 0
s v
s0
0 t
v0
0 t
Prof. Ary de Oliveira

9. Mov. Progressivo e Mov. Retrógrado
s
v
v0
s0
Movimento progressivo
0 t
0 t
s
v
s0
Movimento retrógrado
0 t
v0
0 t
Prof. Ary de Oliveira

10. Propriedade Gráfico S x t
A inclinação, ou tangente do ângulo, do gráfico S x t
para um movimento uniforme (que é uma reta) nos
fornece o valor da velocidade.
s v>0 s v<0
s
s0
S
S
s0 θ s θ
0 t t 0 t t
t t
N N
Cateto Oposto ∆S
v = tg (θ ) ⇒ v = Cateto Adjacente
⇒ v=
∆t
Prof. Ary de Oliveira

11. Propriedade Gráfico v x t
A área formada entre o gráfico v x t e o eixo dos
tempos é numericamente igual a variação dos espaços
( S).
v v
v0 N
∆S = A v > 0 ou v < 0
0 t 0 N t
∆S = A
v0
OBS.: A área formada entre o gráfico v x t e o eixo dos
tempos, em qualquer movimento, é numericamente
igual a variação dos espaços ( S).
Prof. Ary de Oliveira

12. Exercício de Fixação 01
(PSAEAM – 2007) Um submarino submerso detecta um
navio a uma distância de 1500m e dispõe de um torpedo
que se desloca com velocidade constante de 15m/s.
Considerando que o submarino está posicionado na
origem de um sistema de referência e que a equação
horária do torpedo é S = 15t, qual é o tempo necessário
para que o torpedo atinja o navio?
(A) 10 segundos.
(B) 15 segundos.
(C) 1 minuto e 20 segundos.
(D) 1 minuto e 40 segundos.
(E) 1 minuto e 50 segundos.
Prof. Ary de Oliveira

13. Exercício de Fixação 01
(PSAEAM – 2007) Um submarino submerso detecta um
navio a uma distância de 1500m e dispõe de um torpedo
que se desloca com velocidade constante de 15m/s.
Considerando que o submarino está posicionado na
origem de um sistema de referência e que a equação
horária do torpedo é S = 15t, qual é o tempo necessário
para que o torpedo atinja o navio?
(A) 10 segundos.
(B) 15 segundos.
(C) 1 minuto e 20 segundos.
(D) 1 minuto e 40 segundos.
(E) 1 minuto e 50 segundos.
Prof. Ary de Oliveira

14. Exercício de Fixação 02
(PSACN – 2004)
O gráfico acima representa o movimento de dois móveis A
e B a partir de t = 0 s. Considerando que os móveis
encontram-se, inicialmente na mesma posição, pode-se
afirmar que após 30 s, a distância em metros, que os
separa vale:
(A) 180 (C) 100 (E) 0
(B) 120 (D) 60
Prof. Ary de Oliveira

15. Exercício de Fixação 02
(PSACN – 2004)
O gráfico acima representa o movimento de dois móveis A
e B a partir de t = 0 s. Considerando que os móveis
encontram-se, inicialmente na mesma posição, pode-se
afirmar que após 30 s, a distância em metros, que os
separa vale:
(A) 180 (C) 100 (E) 0
(B) 120 (D) 60
Prof. Ary de Oliveira

16. Exercício de Fixação 03
(EEAR – 2011.1 adaptada) O gráfico representa a
variação do módulo da velocidade (V) em função do
tempo (t) de uma partícula.
A distância percorrida pela partícula entre os instantes 0 a
8 s foi, em m, igual a:
(A) 2 (B) 5 (C) 10 (D) 12
Prof. Ary de Oliveira

17. Exercício de Fixação 03
(EEAR – 2011.1 adaptada) O gráfico representa a
variação do módulo da velocidade (V) em função do
tempo (t) de uma partícula.
A distância percorrida pela partícula entre os instantes 0 a
8 s foi, em m, igual a:
(A) 2 (B) 5 (C) 10 (D) 12
Prof. Ary de Oliveira

18. Exercício de Fixação 04
(EEAR – 2011.2) Dois moveis A e B, ambos de
comprimento igual a 2 m, chegam exatamente juntos na
entrada de um túnel de 500 m, conforme mostrado na
figura. O móvel A apresenta uma velocidade constante de
72 km/h e o móvel B uma velocidade constante de 36
km/h. Quando o móvel B atravessar completamente o
túnel, qual será a distância d, em metros, que o móvel A
estará a sua frente? Para determinar esta distância
considere a traseira do móvel A e a dianteira do móvel B.
(A) 498 (B) 500 (C) 502 (D) 504
Prof. Ary de Oliveira

19. Exercício de Fixação 04
(EEAR – 2011.2) Dois moveis A e B, ambos de
comprimento igual a 2 m, chegam exatamente juntos na
entrada de um túnel de 500 m, conforme mostrado na
figura. O móvel A apresenta uma velocidade constante de
72 km/h e o móvel B uma velocidade constante de 36
km/h. Quando o móvel B atravessar completamente o
túnel, qual será a distância d, em metros, que o móvel A
estará a sua frente? Para determinar esta distância
considere a traseira do móvel A e a dianteira do móvel B.
(A) 498 (B) 500 (C) 502 (D) 504
Prof. Ary de Oliveira

20. Exercício de Fixação 05
(EEAR – 2013) Dois pontos materiais A e B tem seus
movimentos retilíneos uniformes descritos no gráfico, da
posição (x) em função do tempo (t), a seguir. A razão entre
o módulo da velocidade de B e o módulo da velocidade de
A é:
(A) 1/2 (B) 1/3 (C) 2/3 (D) 3/2
Prof. Ary de Oliveira

21. Exercício de Fixação 05
(EEAR – 2013) Dois pontos materiais A e B tem seus
movimentos retilíneos uniformes descritos no gráfico, da
posição (x) em função do tempo (t), a seguir. A razão entre
o módulo da velocidade de B e o módulo da velocidade de
A é:
(A) 1/2 (B) 1/3 (C) 2/3 (D) 3/2
Prof. Ary de Oliveira

22. Exercício de Fixação 06
(EsPCEx – 2005) Um caminhão de 10 m de comprimento,
descrevendo um movimento retilíneo e uniforme, ingressa
em uma ponte com uma velocidade de 36 km/h. Passando
20 s, o caminhão conclui a travessia da ponte. O
comprimento da ponte é de:
(A) 100 m
(B) 110 m
(C) 190 m
(D) 200 m
(E) 210 m
Prof. Ary de Oliveira

23. Exercício de Fixação 06
(EsPCEx – 2005) Um caminhão de 10 m de comprimento,
descrevendo um movimento retilíneo e uniforme, ingressa
em uma ponte com uma velocidade de 36 km/h. Passando
20 s, o caminhão conclui a travessia da ponte. O
comprimento da ponte é de:
(A) 100 m
(B) 110 m
(C) 190 m
(D) 200 m
(E) 210 m
Prof. Ary de Oliveira

24. Exercício de Fixação 07
(EsPCEx – 2009) Em uma mesma pista, duas partículas
puntiformes A e B iniciam seus movimentos no mesmo
instante com as suas posições medidas a partir da mesma
origem dos espaços. As funções horárias das posições de
A e B, para S, em metros, e T, em segundos, são dadas,
respectivamente, por SA = 40 + 0,2T e SB = 10 + 0,6T.
Quando a partícula B alcançar a partícula A, elas estarão
a posição:
(A) 55 m (C) 75 m (E) 125 m
(B) 65m (D) 105 m
Prof. Ary de Oliveira

25. Exercício de Fixação 07
(EsPCEx – 2009) Em uma mesma pista, duas partículas
puntiformes A e B iniciam seus movimentos no mesmo
instante com as suas posições medidas a partir da mesma
origem dos espaços. As funções horárias das posições de
A e B, para S, em metros, e T, em segundos, são dadas,
respectivamente, por SA = 40 + 0,2T e SB = 10 + 0,6T.
Quando a partícula B alcançar a partícula A, elas estarão
a posição:
(A) 55 m (C) 75 m (E) 125 m
(B) 65m (D) 105 m
Prof. Ary de Oliveira

26. Fim!
Prof. Ary de Oliveira