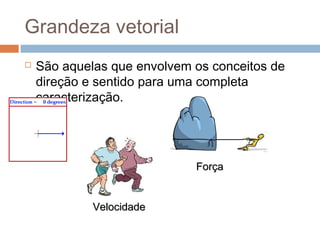
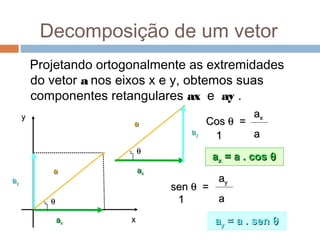
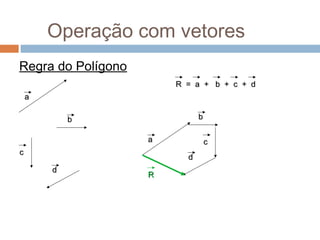
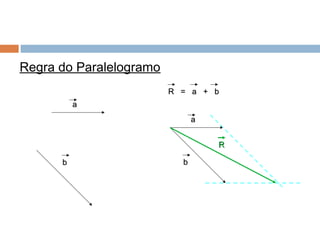
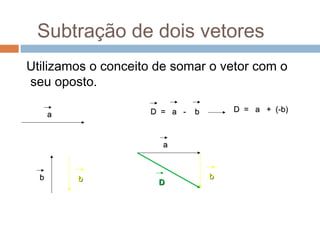
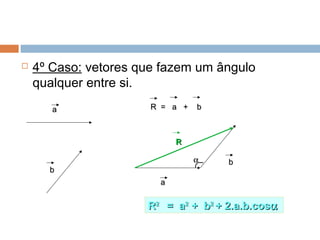
1) O documento discute vetores, que são grandezas que possuem direção e sentido, diferentemente de grandezas escalares que são definidas apenas por valor numérico. 2) Vetores podem ser somados usando a regra do paralelogramo ou do poligono, dependendo de como eles estão orientados um em relação ao outro. 3) Há casos particulares de soma de vetores dependendo de se eles estão na mesma direção, em direções opostas, formando ângulo reto ou em ângulo qualquer.

1. VETORES
Introdução

2. Grandeza escalar
 Aquelas que são definidas por um valor
numérico e por uma unidade.
Tempo
Temperatura
Energia
Massa

3. Grandeza vetorial
 São aquelas que envolvem os conceitos de
direção e sentido para uma completa
caracterização.
Força
Velocidade

4. Vetor
É um segmento de reta geometricamente
orientada, ou seja, possui módulo, sentido e
direção.
a = 4 unidades
Módulo: 4 unidades
Sentido: para direita
Direção: horizontal

5. Operação com vetores
Regra do Polígono
R = a + b + c + d
a
b b
a c
c
d
d
R

6. Regra do Paralelogramo
R = a + b
a
a
R
b b

7. Casos Particulares
 1º Caso: vetores com a mesma direção e o
mesmo sentido.
a R = a + b
b a
b
R
R = a + b

8.  2º Caso: vetores com a mesma direção e
sentidos opostos.
R = a + b
a
a
b
R
b
R = a - b

9.  3º Caso: vetores que fazem um ângulo de 90º
entre si.
a R = a + b
b R
b
a
R2 = a2 + b2

10.  4º Caso: vetores que fazem um ângulo
qualquer entre si.
a R = a + b
R
α b
b
a
R2 = a2 + b2 + 2.a.b.cosα

11. Subtração de dois vetores
Utilizamos o conceito de somar o vetor com o
seu oposto.
D = a - b D = a + (-b)
a
a
b b b
D

12. Decomposição de um vetor
Projetando ortogonalmente as extremidades
do vetor a nos eixos x e y, obtemos suas
componentes retangulares ax e ay .
y ax
a Cos θ =
ay a
1
θ
ax = a . cos θ
a ax
ay ay
sen θ =
θ 1 a
ax x ay = a . sen θ

13. Acesse o blog e divirta!!!