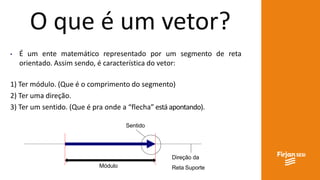
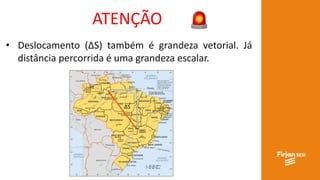
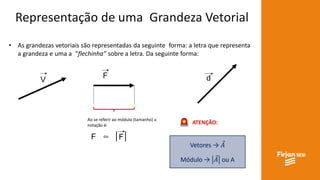
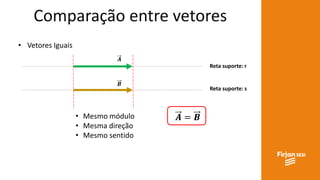
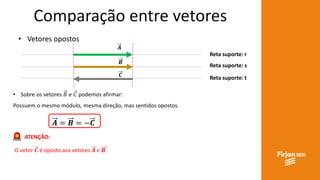
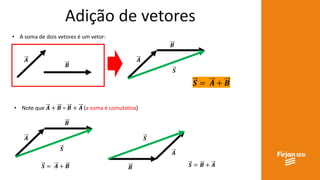
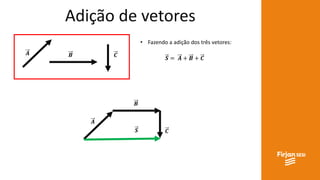
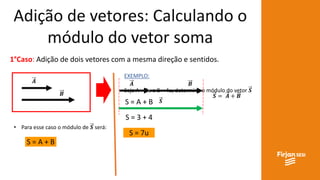
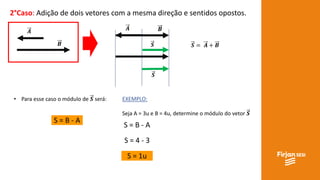
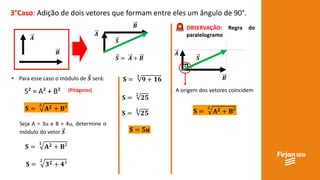
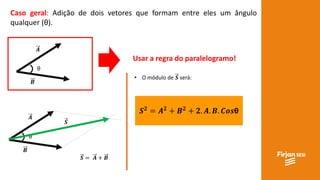
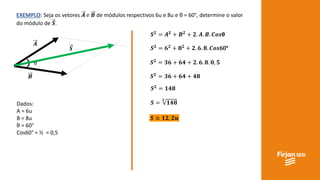
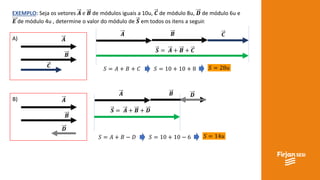
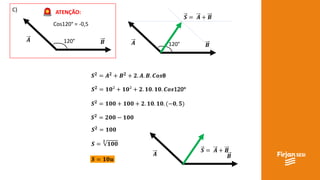
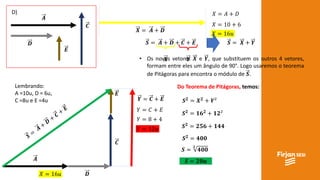
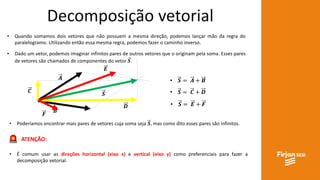
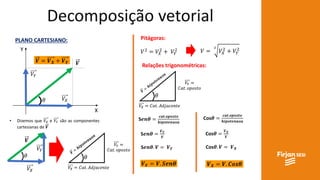
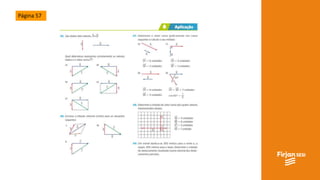
O documento aborda conceitos de vetores e grandezas físicas, enfatizando a diferença entre grandezas escalares e vetoriais. Ele explica a adição de vetores, incluindo casos de vetores em direções opostas e a aplicação do teorema de Pitágoras. Também aborda a decomposição vetorial e como encontrar componentes cartesianas utilizando relações trigonométricas.