1) O documento discute os conceitos fundamentais da trigonometria, incluindo a origem histórica da trigonometria, medidas de ângulos, relações métricas no triângulo retângulo e funções trigonométricas.
2) Apresenta definições de ângulo, medição de ângulos, relações nos triângulos retângulos que dão origem às funções seno, cosseno e tangente.
3) Explica conceitos como medida e tipos de arcos, ciclo trigonométrico e ar






![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 7
1.13 Arcos Côngruos
Dois arcos trigonométricos são ditos côngruos,
quando a diferença entre eles é um número múltiplo
de 360º. Assim é que sendo x e y dois arcos
trigonométricos, eles serão côngruos se e somente se:
x y = k . 360º , onde k é um número inteiro.
Portanto, para descobrir se dois arcos são côngruos,
basta verificar se a diferença entre eles é um múltiplo
de 360º (ou 2 radianos, pois 2 rad = 360º).
Obs. Arcos de uma mesma família são côngruos.
Exemplo:
Os arcos 2780º e 1700º, são côngruos, pois:
2780º 1700º = 1080º e
1080º é divisível por 360º (1080º / 360º = 3).
Exercício resolvido:
Quantos são os valores de m compreendidos entre 30
e 40, que tornam côngruos os arcos de medidas
(4m+10).180º e (3m2).180º ?
Solução:
Pela definição de arcos côngruos dada, deveremos ter:
(4m+10).180º (3m2).180º = k . 360º, com k.
720m + 1800 [540m 360] = k . 360
720m + 1800 540m + 360 = k . 360
180m + 2160 = k . 360
180m = k . 360 2160
m = 2k 12
Mas, pelo enunciado, temos 30 < m < 40. Logo:
30 < 2k 12 < 40
42 < 2k < 52
21 < k < 26 k = 22, 23, 24 ou 25.
Existem 4 valores possíveis para k e, portanto, também
4 valores possíveis para m, já que m = 2k 12.
Portanto:
m = 32, 34, 36 e 38.
Exercícios:
11) Testes: Verdadeiro Falso
a) Os arcos de 4200º e 3480º são côngruos
b) Os arcos de ( 420º ) e 300º são côngruos.
c) O arco de 10.002º pertence ao segundo
quadrante.
d) O arco de ( 200º) pertence ao segundo
quadrante.
R: Verdadeiro: a, b e d.
1.14 Arcos de mesma origem, simétricos em relação
ao eixo OX
Sejam AM e 'AM arcos no círculo trigonométrico,
com A=( 1, 0 ) e os pontos M e M' simétricos em relação
ao eixo horizontal OX.
Se a medida do arco AM é igual a m, então a medida do
arco 'AM é dada por: µ( 'AM ) = 2m.
1.15 Arcos de mesma origem, simétricos em
relação ao eixo OY
Sejam AM e 'AM arcos no círculo trigonométrico,
com A = ( 1 ,0 ) e os pontos M e M' simétricos em
relação ao eixo vertical OY. Se a medida do arco AM
for igual a m, então a medida do arco 'AM será dada
pela expressão µ( 'AM ) = m.
1.16 Arcos com a mesma origem e extremidades
simétricas em relação à origem
Sejam AM e 'AM arcos no círculo trigonométrico,
com A=( 1 ,0 ) e os pontos M e M' simétricos em
relação a origem (0,0). Se a medida do arco AM é igual
a m, então a medida do arco 'AM é dada por: µ( 'AM )
= +m.](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-7-320.jpg)
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 8
1.17 Funções circulares
As funções circulares constituem o objeto
fundamental da trigonometria circular e são
importantes devido à sua periodicidade pois elas
podem representar fenômenos naturais periódicos,
como as variações da temperatura terrestre, o
comportamento ondulatório do som, a pressão
sanguínea no coração, os níveis de água dos oceanos,
etc.
1.18 Função periódica
Dizemos que uma função f(x) é periódica se existe
um número real T 0 tal que f ( x + T ) = f ( x )
para todo x Dom (f ).
O número T é chamado período da função f(x).
O gráfico de uma função periódica se repete a cada
intervalo de comprimento T.
Exemplos de gráficos de funções periódicas são
observadas nas Figuras abaixo:
1.19 Função limitada
Uma função f de domínio A contido em R é limitada,
se existe um número real positivo L, tal que para todo
x em A, valem as desigualdades:
L < f ( x ) < L
Esta última expressão pode ser escrita como:
| f(x) | < L.
1.20 Função par
Uma função f é uma função par, se para todo x do
domínio de f:
f(x) = f(x)
Funções pares são simétricas em relação ao eixo vertical
OY.
Exemplo:
A função f(x) = 2x , pois: 2 2f( x) x x
1.21 Função ímpar:
Uma função f é uma função ímpar, se para todo x do
domínio de f:
f(x) = f(x)
Funções ímpares são simétricas em relação à origem
(0,0) do sistema de eixos cartesiano.
Exemplo:
A função f(x) = x é uma função par, pois f(x) = x =
f(x).
1.22 Função seno
Definição: Chamamos de função seno , a função
:f que, a cada número real x, associa o seno
desse número.
:f
f(x) = sen x
A função é denotada por f(x) = sen(x) ou y = sen(x).
Gráfico: O gráfico da função f(x) = sen x, denomina-se
senóide. Para construir o gráfico da função, atribuímos
valores para x e encontramos f(x). Segue uma tabela
com valores de f no intervalo [0,2].
x y = senx
0 0
2
1
0
2
3 -1
2 0
Na figura, o segmento Oy' que mede sen(x), é a projeção
do segmento OM sobre o eixo OY.](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-8-320.jpg)
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 9
onde:
Dom:
Im: 1,1
P = 2 rad ( A função seno é periódica, pois:
sen ( x+ 2) = sen x.)
Crescente: [ 0,
2
] [
2
3 ,2]
Decrescente: [
2
,
2
3 ]
Limitada: 1 < sen x < 1
Ímpar : sen(x) = sen(x)
Para todo x em R e para todo k em Z:
sen(x) = sen(x+2) = sen(x+4) =...= sen(x+2k)
Completamos o gráfico da função seno, repetindo os
valores da tabela em cada intervalo de medida 2,
teremos:
Sinal:
Intervalo 0,
2
,
2
3
,
2
3
,2
2
Função
seno
positiva positiva negativa negativa
Exercícios Resolvidos:
01) Construa o gráfico da função f(x) = 2 sen x,
dando o domínio, imagem, intervalos de
crescimento, decrescimento e o período.
Resolução:
Observe a tabela abaixo, onde atribuímos valores
para x e encontramos f(x).
x senx 2senx
0 0 0
2
1 2
0 0
2
3 1 2
2 0 0
O gráfico desta função está apresentado na figura
abaixo, onde comparamos o comportamento da função
f(x)= 2sen x, com a função f(x) = sen x.
onde:
Dom:
Im: 2,2
P = rad2
Crescente: [
2
,
2
3 ]
Decrescente: [ 0,
2
] [
2
3
,2]
Obs. A função f(x) = 2 sen x modifica sua amplitude
em relação à função f(x) = senx.
02) Construa o gráfico da função f(x) =
2
xsen ,
dando o domínio, imagem, intervalos de
crescimento, decrescimento e o período.
Resolução:
Fazendo x t x t
2 2
](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-9-320.jpg)
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 10
Observe a tabela abaixo,onde atribuímos valores para
x e encontramos f(x).
2
tx
t y = sen t
2
0 0
2
1
2
3 0
2 3
2
1
2
5 2 1
O gráfico desta função está apresentado na figura
abaixo, onde comparamos o comportamento da
função f(x)=
2
xsen com a função f(x) = sen x.
onde:
Dom:
Im: 1,1
P = rad2
Crescente: [
2
, ] [2 ,
5
2
]
Decrescente: [ , 2 ]
Exercícios:
12) O gráfico abaixo corresponde à função:
R: f(x)=2.senx
13) Construir os gráficos e dar o domínio, imagem e o
período das função:
x
a)f (x) sen
2
b) f(x) 2 sen x
c)f (x) senx
d)f (x) 2 sen(2x )
Respostas:
E-15:
a)
b)
c)
d)](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-10-320.jpg)
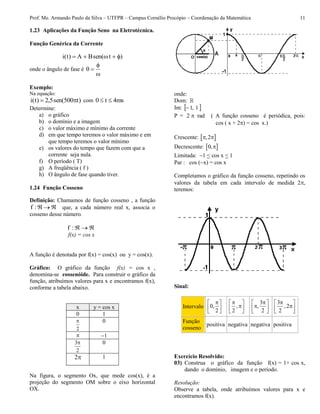
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 12
x cos x 1+cos x
0 1 2
2
0 1
1 0
2
3 0 1
2 1 2
O gráfico desta função está apresentado na figura
abaixo, onde comparamos o comportamento da
função f(x)= 1+cos x com a função f(x) =cos x.
onde:
Dom:
Im: [ ]20,
P = rad2
Crescente: ,2
Decrescente: 0,
Obs. A função f(x) = 1 + cos x desloca-se em 1
unidade no eixo y em relação ao gráfico da função
f(x)= cos x.
04) Construa o gráfico da função f(x) =
x
cos
2
,
dando o domínio, imagem e o período.
Resolução:
Fazendo
x
t x 2t
2
Observe a tabela, onde atribuímos valores para x e
encontramos f(x).
x t
cos
x
2
0 0 1
2
0
2 1
3
2
3 0
4 2 1
O gráfico desta função está apresentado na figura
abaixo, onde comparamos o comportamento da função
f(x) = cos x com a função f(x) = cos
x
2
.
RESUMINDO
Considerando as funções:
y = a + b sen ( mx + n )
y = a + b cos ( mx + n ).
Temos:
Dom:
C.D:
Im: ba,ba , b> 0
P = rad
m
2
Exercícios:
14) Construir os gráficos e dar o domínio, imagem e o
período das função:
a) y = cos x
b) y = cos 2x](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-12-320.jpg)
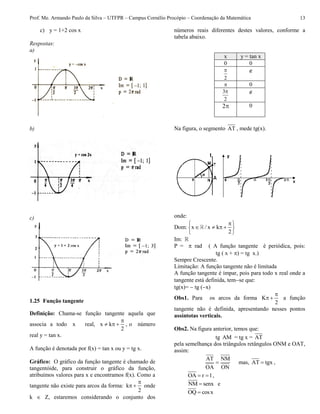
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 14
Substituindo na expressão
tgx senx
1 cosx
, teremos:
senx
tgx
cosx
, onde x K
2
Completamos o gráfico da função tangente, repetindo
os valores da tabela na mesma ordem em que se
apresentam, teremos:
Sinal:
Intervalo [0, /2] [/2, ] [,3/2] [3/2,2]
Função
tangente
positiva negativa positiva negativa
1.26 Função cotangente
Definição: Chama-se função cotangente aquela que
associa a todo x real, x k , o número real
y = cot x.
A função é denotada por f(x) = cotg x ou y = cot x.
Gráfico: O gráfico da função cotangente é chamado
de cotangentóide, para construir o gráfico da função,
atribuímos valores para x e encontramos f(x). Como a
cotangente não existe para arcos da forma: k, onde
kZ, estaremos considerando o conjunto dos números
reais diferentes destes valores, conforme a tabela
abaixo.
x y = cot x
0
2
0
2
3 0
2
Na figura, o segmento BS , mede cotg(x).
onde:
Dom: x / x k
Im:
P = rad ( A função tangente é periódica, pois:
cotg ( x + ) = cotg x.)
Sempre Decrescente.
Limitação: A função tangente não é limitada.
A função tangente é ímpar, pois para todo x real onde a
tangente está definida, temse que:
cotg(x)= cotg (x)
Obs1. Para os arcos da forma K a função tangente
não é definida, apresentando nesses pontos assíntotas
verticais.
Obs 2. Por analogia ao que foi feito na tangente,
podemos mostrar que
cosx 1
cot x
senx tgx
Completamos o gráfico da função cotangente, repetindo
os valores da tabela na mesma ordem em que se
apresentam, teremos:
Sinal:
Intervalo [0, /2] [/2, ] [,3/2] [3/2,2]
Função
tangente
positiva negativa positiva negativa](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-14-320.jpg)
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 15
1.27 Função Secante
Definição: Chama-se função secante aquela que
associa a todo x real, x k
2
, o número
real y = sec x.
A função é denotada por f(x) = sec x ou y = sc(x)
Gráfico: Para construir o gráfico da função,
atribuímos valores para x e encontramos f(x). Como a
secante não existe para arcos da forma: k
2
onde
kZ, estaremos considerando o conjunto dos números
reais diferentes destes valores, conforme a tabela
abaixo.
x y = sec x
0 1
4
2
2
3
4
2
1
5
4
2
2
3
7
4
2
2 1
Gráfico: O segmento OV mede sec(x).
onde:
Dom: x / x k
2
Im: , 1 1,
P = 2 rad
Crescente: 0,
Decrescente: ,2
Limitação: A função secante não é limitada
A função secante é par, pois para todo x real onde a
secante está definida, temse que: séc x= sec (x)
Obs1. Para os arcos da forma K
2
a função secante
não é definida, apresentando nesses pontos assíntotas
verticais.
Obs 2. Por analogia ao que foi feito na tangente,
podemos mostrar que
1
secx
cosx
Completamos o gráfico da função secante, repetindo os
valores da tabela na mesma ordem em que se apresentam,
teremos:
Sinal:
Intervalo [0, /2] [/2, ] [,3/2] [3/2,2]
Função
secante
positiva negativa negativa positiva
1.28 Função Cossecante
Definição: Chama-se função cosssecante aquela que
associa a todo x real, x k , o número real
y = cossec x.
A função é denotada por f(x) = cossec x ou y = csc(x)
Gráfico: Para construir o gráfico da função, atribuímos
valores para x e encontramos f(x). Como a secante não
existe para arcos da forma: k onde k Z, estaremos
considerando o conjunto dos números reais diferentes
destes valores, conforme a tabela abaixo.](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-15-320.jpg)
![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 16
x y =cossec x
0
4
2
2
1
3
4
2
5
4
2
2
3
1
7
4
2
2
Gráfico: O segmento OB mede cossec(x).
onde:
Dom: x / x k
Im: , 1 1,
P = 2 rad
Crescente:
3
, ,
2 2
Decrescente:
3
0, ,2
2 2
Limitação: A função cossecante não é limitada.
A função cossecante é ímpar, pois para todo x real
onde a cossecante está definida, temse que:
cossec(x) = cosses (x)
Obs1. Para os arcos da forma K a função
cossecante não é definida, apresentando nesses pontos
assíntotas verticais.
Obs 2. Por analogia ao que foi feito na cotangente,
podemos mostrar que
1
cossecx
sen x
Completamos o gráfico da função secante, repetindo os
valores da tabela na mesma ordem em que se apresentam,
teremos:
Sinal:
Intervalo [0, /2] [/2, ] [,3/2] [3/2,2]
Função
cossecante
positiva positiva negativa negativa
1.29 Resumo de Trigonometria
Quanto ao Domínio
Função seno e cosseno
Dom f =
Função tangente e secante
Dom f= { x / x K
2
}
Função cotangente e cossecante
Dom f= { x / x K }
Quanto ao Período
Função seno, cosseno, secante e cossecante:
P = 2
Função tangente e cotangente:
P =
Exercícios:
17) Determine o domínio das funções abaixo:
a) y 2tg 2x
3
b) y =
x 3
1 cossec
3 2
c) y = 3 + sec 2x
6
](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-16-320.jpg)

![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 18
Dividindo a relação fundamental nº 01 por sen2
(x) e
por cos2
(x) e aplicando os conceitos de tangente,
cotangente, secante e cossecante, teremos outras duas
relações fundamentais, a saber:
e
Exemplos:
01) Simplifique a expressão:
cossecx senx
cotgx secx
Solução:
Utilizando os conceitos vistos, temos:
2
2 2
1 1 sen x
senx
senx senx 1 sen x cos x
cosx 1 1
.
senx cosx senx
02) Sendo x um arco tal que cos x = tgx , calcule
senx.
Solução:
Sabemos que tgx =
senx
cosx
Substituindo tgx por cosx (dado do problema), vem:
cosx =
senx
cosx
donde vem: cos2
x = senx.
Mas, cos2
x = 1 sen2
x .
Substituindo, fica: 1 sen2
x = senx.
Daí, vem: sen2
x + senx 1 = 0
Fazendo senx = y e substituindo: y2
+ y 1 = 0.
Resolvendo esta equação do 2º grau, fica:
Como y = senx e , temos somente um dos valores
acima satisfazendo o problema, ou seja:
5 1
senx ,
2
que é a resposta procurada.
03) Para que valor de m a expressão:
y = (m 1)(sen4
x cos4
x) + 2cos2
x + m.cosx
2.cosx + 1 é independente de x?
Solução:
Podemos escrever:
y = (m 1)[(sen2
x cos2
x)(sen2
x + cos2
x)] + 2cos2
x +
mcosx 2cosx + 1
Como sen2
x + cos2
x = 1, substituindo, fica:
y = (m1)(sen2
x cos2
x) +2cos2
x + mcosx 2cosx +1
y = msen2
x mcos2
x sen2
x + cos2
x + 2cos2
x +
mcosx
2cosx + 1
Escrevendo tudo em função de cosx, lembrando que
sen2
x = 1 cos2
x, vem:
y = m(1 cos2
x) mcos2
x (1 cos2
x) + cos2
x +
2cos2
x + mcosx 2cosx + 1
y = m mcos2
x mcos2
x 1 + cos2
x + cos2
x + 2cos2
x
+ mcosx 2cosx + 1
Simplificando os termos semelhantes, fica:
y = m + (4 2m)cos2
x + (m 2)cosx
Para que a expressão acima seja independente de x,
deveremos ter necessariamente 4 2m = 0 e m 2 = 0
portanto: m = 2, que é a resposta procurada.
Exercícios:
20) Dado
3
sen x
5
, com x
2
, calcule as
demais funções.
R.:
4
cos x
5
;
3
tgx
4
;
5
sec x
4
;
5
csc x
3
;
4
cot x
3
21) Sendosecx 2 e x
2
, calcule tgx e senx.
R.:
2
tgx 1 e senx=
2
22) Sendo cot a = 3 e
3
a
2
,calcule o valor de :
seca cosseca
y
cosseca cosa
R.:
1
y
3
23) Sendo 2 232sen x 16cos x 25 , calcule o valor do
senx. R.:
3
y senx
4
24) Calcule m, de modo que se tenha simultaneamente:
m 2
senx
8
e
5 m
cosx
2
. R.: m =2
25) Para que valor de m a expressão:
y = m(sen4
x cos4
x) + 2cos2
x 1 + m é
independente de x?
R.: m=1
1.32 Identidades Trigonométricas
Uma igualdade entre expressões trigonométricas é chamada
Identidade, quando a igualdade é satisfeita para todos os
valores que pertencem aos domínios das funções que
envolvem.
Para provarmos uma identidade trigonométrica,
podemos proceder de duas maneiras:
tg2
x + 1 = sec2
x cotg2
x + 1 = cosec2
x](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-18-320.jpg)

![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 20
30) Simplificar a seguinte expressão:
y = cos(x 90º) cos(x 270º). R: 2senx
31) Calcule:
a)cos 15º R:
6 2
4
b) tg 75º R: 2 3
c) sen 105º R:
6 2
4
32) Sabendo que
13
12
acos , a + b = 120º e
0 a
2
, calcule o cos b. R:
12 5 3
26
ARCO DUPLO
Fazendo a = b nas fórmulas da soma, vem:
2 2cos(2a) cos a sen a
sen(2a) 2sena.cosa
2
2.tga
tg(2a)
1 tg a
Obs. A fórmula acima somente é válida para tg a 1
e tg a 1, já que nestes casos o denominador seria
nulo.
EXEMPLOS:
a) sen4x = 2.sen2x.cos2x
b) senx = 2.sen(x/2).cos(x/2)
c) cosx = cos2
(x/2) - sen2
(x/2)
d) cos4x = cos2
2x - sen2
2x
EXERCÍCIOS:
33) Dado tg x 2 1 , calcule tg 2x . R: 1
34) Sendo sen x + cos x =
5
6
, calcular: sen 2x.
R:
11
25
35) Calcular sen(2a+b) , sendo sen a =
3
5
e sen b =
5
,
13
0 a e b
2 2
.
R:
253
325
ARCO METADE
Vamos agora achar as funções trigonométricas da
metade de um arco, partindo das anteriores.
Cosseno do arco metade: Sabemos que:
cos2a = cos2
a sen2
a
Substituindo sen2
a, por: 1 cos2
a e sen2
a + cos2
a por 1,
vem:
cos2a = 2.cos2
a 1, isolando cos2
a :
cos2
a = (1+cos2a) / 2
Fazendo a = x/2, vem, cos2
(x/2) = [1+cosx]/2.
Podemos escrever então a fórmula do cosseno do arco
metade como:
x 1 cosx
cos
2 2
Seno do arco metade: De maneira análogo, obtemos o
seno e do arco metade.
x 1 cosx
sen
2 2
Tangente do arco metade: Dividindo membro a
membro as equações anteriores, lembrando que
tg(x/2) = sen(x/2) / cos(x/2), vem:
x 1 cosx
tg
2 1 cosx
Obs: o sinal algébrico de cada expressão, vai depender
do quadrante ao qual pertence o arco x/2.
Exercício resolvido:
Sabendo que sen x =
4 3
e <x<
5 2
, calcular tg
x
2
.
Resolução:
1º passo: determinar o quadrante de
x
2
:
Se
3
<x<
2
, dividindo todos os termos por 2,
temos:
x 3
2 2 4
, isto é:
x
2
é um arco do 2º quadrante.
2º passo: cálculo de cos x:
2
24
cos x 1
5
3
cosx
5
3º passo: cálculo de tg
x
2
2 5x
sen
x 52tg 2
x2 5cos
2 5
](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-20-320.jpg)



![Prof. Me. Armando Paulo da Silva – UTFPR – Campus Cornélio Procópio – Coordenação da Matemática 24
cossec x = 2
2 sec ( x+ 20º) = 4
sen x 1
6
R: a) 360 270 S x / x k. º º
b) 180 S x / x k. º
c) 120 50 S x / x k. º º
d) 360 225 360 315 S x / x k. º º ou x k. º º
e) 360 80 360 40 S x / x k. º º ou x k. º º
f)
2
2
3
S x / x k.
41) Resolver as equações trigonométricas:
a) 22sen x 3senx 1 0
b) 23tg x 5 7secx
c) 2 2cos 3x 2sen 3x 2
d) 4 4 5
sen x cos x
8
R:
360 90
360 30
360 150
a ) S x / x k. º º ou
x / x k. º º ou
x / x k. º º
b) 360 60 S x / x k. º º
c) 60 30 S x / x k. º º
d) 90 30 S x / x k. º º
1.36 Funções circulares inversas
Sabemos que uma função f de domínio D possui inversa
somente se f for bijetora. As funções circulares, conforme
definidas, não são bijetoras, mas podemos tomar
subconjuntos desses domínios para gerar novas
função que possuam inversas.
Exemplo:
A função f(x) = sen x não é bijetora em seu domínio
de definição que é o conjunto dos números reais, pois
para um valor de y correspondem infinitos valores de
x, isto quer dizer que não podemos definir a inversa
de sen(x) em seu domínio. Devemos então restringir o
domínio para um subconjunto dos números reais onde
a função é bijetora.
FUNÇÃO ARCOSENO
Consideremos a função f(x) = sen x, com domínio no
intervalo [/2,/2] e imagem no intervalo [1,1].
A função inversa de f, denominada arco seno de x,
definida por f1
:[1,1] [/2,/2] é denotada por
f1
(x) = arcsen(x).
Lê-se: “ o arco cujo seno é x”
Gráfico da função arcoseno: o gráfico da inversa é
simétrico do gráfico de y = senx em relação à bissetriz
do 1º e 3º quadrantes.
Função arcocosseno
Seja a função g(x) = cos x, com domínio [0,] e
imagem [1,1]. De modo análogo ao estudo da função
seno, podemos definir a função de f, denominada arco
cosseno de x, definida por g1
:[1,1] ] [0,] e
denotada por: g1
(x) = arccos(x).
Lê-se: “ o arco cujo cosseno é x”.
Gráfico da função arcocosseno:
Função arcotangente
Dada a função f(x) = tan(x), com domínio (/2,/2) e
imagem em R, a função inversa de f, denominada
arcotangente é definida por f1
:R (/2,/2) e
denotada por: f1
(x) = arctan(x)
Lê-se: “ o arco cuja tangente é x”.](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-24-320.jpg)
 e
denotada por: f1
(x) = arccot(x)
Lê-se: “ o arco cuja cotangente é x”.
Gráfico da função arcocotangente:
Exemplos:
01) Calcular arc tg 3
SOLUÇÃO:
arc tg 3
tg 3 e
2 2
3
02) Calcular
1
y tg arc.sen
2
Solução:
1
arc sen
2
1
sen
2
e
2 2
6
Como y = tg
3
y tg y
6 3
03) Achar o domínio e o conjunto imagem da função
y = arc sen ( 4x 3)
solução:
y = arc sen ( 4x 3) seny 4x 3 e
y
2 2
1 seny 1 1 4x 3 1
2 4x 4
1
x 1
2
Logo,
1
D x / x 1 e
2
Im `y / y
2 2
Exercícios:
42) Calcular nos seguintes casos:
a)
1
arc sen
2
b)
3
arc cos
2
c) arc tg 3
d) 2arc tg 3
R: a)
6
; b)
5
6
; c)
3
d)
2
43) Calcular o valor de y para:
a)
1
y cos arc sen
3
b)
5
y tg arc cos
13
c)
3
y tg arc sen
5
R:a)
2 2
3
; b)
12
5
c)
3
4
44) Determinar do domínio e o conjunto imagem das
funções:
y = arc sen 2x
y = arc cos ( 3x 1)
y = arc tg
3
4
x
R:a)
1 1
2 2
D x / x
e
2 2
Im ` y / y
b)
2
0
3
D x / x e
0Im ` y / y ](https://image.slidesharecdn.com/apostilatrigonometriaarmando-190717033142/85/Apostila-trigonometria-armando-25-320.jpg)


