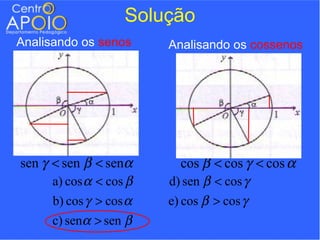
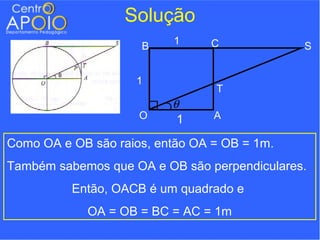
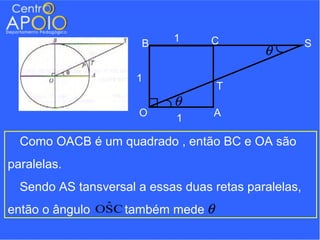
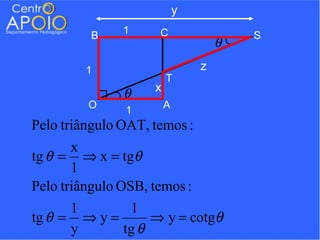
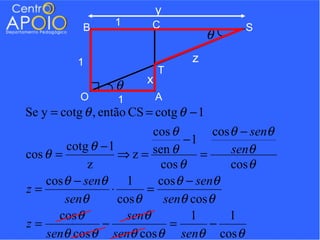
O documento contém uma série de exercícios de trigonometria, abordando conversões entre radianos e graus, ângulos em relógios atrasados e relações trigonométricas aplicadas a figuras geométricas. Os estudantes são desafiados a resolver problemas utilizando fórmulas trigonométricas e regras de três, além de relacionar ângulos e suas respectivas funções. A abordagem é prática e destina-se a ajudar alunos do 3º ano a dominar conceitos fundamentais da trigonometria.

1. Apostila 1 – Qi - 3º ano
Trigonometria

2. 29) Quantos graus mede aproximadamente um
ângulo de 0,105 radianos?
a)2
b)4
c)6
d)8
e)10

3. 29) Quantos graus mede aproximadamente um
ângulo de 0,105 radianos?
a)2
dados Ângulo = 0,105 rad
b)4
c)6 O que se Medida do
d)8 pede? ângulo em graus
e)10

4. Solução
Já sabemos que π rad equivale a 180º. Então,
basta fazer a regra de três:
π 180º
x=
180º.0,105
0,105 x π
Como π = 3,14, então temos que :
180.0,105
x= = 6,01 Letra c
3,14

5. 30) Num relógio que funciona precisamente o
ponteiro dos minutos desceve um ângulo de
360º no tempo de 1 hora. Num relógio que está
atrasando 2 minutos por dia, no tempo de 1
hora o ponteiro dos minutosdescreve um
ângulo de:
a) 358º
b) 359º
c) 359º 50’
d) 359º 30’
e) 359º 48’

6. 30) Num relógio que funciona precisamente o
ponteiro dos minutos descreve um ângulo de
360º no tempo de 1 hora. Num relógio que está
atrasando 2 minutos por dia, no tempo de 1
hora o ponteiro dos minutos descreve um
ângulo de:
a) 358º Relógio atrasa 2
dados
b) 359º minutos por dia
c) 359º 50’
O que se Ângulo que o
d) 359º 30’
pede? relógio descreve
e) 359º 48’ em 1 hora

7. Solução
Pra saber o ângulo que ele descreve em uma
hora, precisamos saber quantos tempo ele atrasa
por hora.
24 h 2 min 2.1
x= x = 5 segundos
1h x 24
Agora é só saber quantos graus correspondem
a 5 segundos:
60” 6º 5.6
x= x = 0,5º = 30'
5” x 60
Letra c

8. 31) (UERJ) Observe a bicicleta e a tabela
trigonométrica:
Os centros das rodas estão a uma distância de
PQ igual a 120 cm e os raios PA e QB medem,
respectivamente, 25 cm e 52 cm. De acordo com a
tabela, o ângulo Ô tem o seguinte valor:
a) 10º b) 12º c) 13º d) 14º

9. 31) (UERJ) Observe a bicicleta e a tabela
trigonométrica:
Os centros das rodas estão a uma distância de
PQ igual a 120 cm e os raios PA e QB medem,
respectivamente, 25 cm e 52 cm. De acordo com a
tabela, o ângulo Ô tem o seguinte valor:
a) 10º b) 12º c) 13º d) 14º

10. PQ = 120cm
PA = 25 cm
dados
QB = 52 cm
PA e QB são raios
O que se
Ângulo Ô
pede?

11. Solução
Olhando a figura, sabemos que para achar o ângulo
Ô, devemos usar as razões trigonométricas, de acordo
com a tabela. Porém, para isso, temos que achar o
valor de OP ou AO antes.
Q
120
P
52
x 25
O
A B
Note que os triângulos OAP e OBQ são semelhantes,
então:
52 120 + x
= ⇒ x = 111,11
25 x

12. 25
120
Q sen Ô =
P
111,11
111,11 52
25 sen Ô = 0,225
O
A B
Verificando a tabela, percebemos que do ângulo
cujo seno vale 0,225 é o que mede 13º.
Logo, Ô = 13º  letra c

13. 32) (UNIRIO) Ao ser indagado sobre o valor
de sen 45º,
um estudante passou assim:
30º +60º sen30º + sen60º
45º = sen45º =
2 2
Continuando como raciocínio o estudante encontrou
como resposta:
a) Um valor menor que o correto, diferente da metade
do correto
b) O valor correto
c) A metade do valor correto
d) O dobro do valor correto
e) Um valor maior que o correto, diferente do dobro do
correto

14. 32) (UNIRIO) Ao ser indagado sobre o valor
de sen 45º,
um estudante passou assim:
30º +60º sen30º + sen60º
45º = sen45º =
2 2
Continuando como raciocínio o estudante encontrou
como resposta:
a) Um valor menor que o correto, diferente da metade
do correto
b) O valor correto
c) A metade do valor correto
d) O dobro do valor correto
e) Um valor maior que o correto, diferente do dobro do
correto

15. Fórmula para
dados
calcular sen 45º
Comparação entre o
O que se
valor calculado e o valor
pede?
que conhecemos

16. Solução
Resposta do estudante:
sen 30º + sen 60º
sen 45º =
2
1 3
+
sen 45º = 2 2 = 1+ 3 ⋅ 1 = 1+ 3
2 2 2 4
1 + 1,7
sen 45º = = 0,675
4
2 1,4
Sabemos que sen 45º = = = 0,7
2 2
Logo, a resposta é a letra a: um valor menor que
o correto, diferente da metade do correto.

17. 33) (UFF) Considere os ângulos
representados no círculo:
Pode-se afirmar que:
a) cos α < cos β
b) cos γ > cos α
c) senα > sen β
d) sen β < cos γ
e) cos β > cos γ

18. 33) (UFF) Considere os ângulos
representados no círculo:
Pode-se afirmar que:
a) cos α < cos β Representação dos
dados
b) cos γ > cos α arcos no círculo
c) senα > sen β Comparação
O que se
d) sen β < cos γ entre os senos e
pede?
e) cos β > cos γ os cossenos

19. Solução
Analisando os senos Analisando os cossenos
sen γ < sen β < senα cos β < cos γ < cos α
a) cos α < cos β d) sen β < cos γ
b) cos γ > cos α e) cos β > cos γ
c) senα > sen β

20. 34) Se tg x = 3/4 e π < x < 3π / 2 , o valor de
cos x – sen x é:
a) 7/5
b) - 7/5
c) - 2/5
d) 1/5
e) -1/5

21. 34) Se tg x = 3/4 e π < x < 3π / 2 , o valor de
cos x – sen x é:
a) 7/5 tg x = 3/4
b) - 7/5 dados X está no 3º
c) - 2/5 quadrante
d) 1/5
O que se cos x – sen x
e) -1/5 pede?

22. Solução
Para calcular seno e cosseno de x, precisamos
calcular a hipotenusa.
a Pelo Teorema de Pitágora temos:
3
a2 = 3 2 + 4 2  a = 5
x
4 3º quadrante
3 4
sen x = − e cos x = −
5 5
4 3 1
Então, cos x - sen x = − + = − letra e
5 5 5

23. tg a + tg b
35) =
cotg a + cotg b
a) tg a . tg b
b) cotg a . cotg b
c) 1
d) 2
e) sec a . sec b

24. Solução
sen a sen b
+
tg a + tg b cos a cos b =
=
cotg a + cotg b cos a + cos b
sen a sen b
sen a cos b + sen b cos a sen a sen b
= ⋅ =
cos a cos b sen a cos b + sen b cos a
sen a cos b + sen b cos a sen a sen b
= ⋅ =
cos a cos b sen a cos b + sen b cos a
sen a sen b
= = tg a tg b letra a
cos a cos b

25. 36) (UFRJ) A figura mostra uma circunferência de 1m
de raio e centro O, à qual pertencem os pontos A, B
e P, sendo AO perpendicular BO; BS e AT são
retas tangentes a essa circunferência.
Determine o perímetro do polígono AOBSTA em
função do ângulo θ .

26. 36) (UFRJ) A figura mostra uma circunferência de 1m
de raio e centro O, à qual pertencem os pontos A, B
e P, sendo AO perpendicular BO; BS e AT são
retas tangentes a essa circunferência.
Determine o perímetro do polígono AOBSTA em
função do ângulo θ .

27. Raio = 1m
dados AO perpendicular a BO
BS e AT são tangentes
O que se O perímetro
pede? de AOBSTA

28. Solução
1 C
B S
1
T
θ
O 1 A
Como OA e OB são raios, então OA = OB = 1m.
Também sabemos que OA e OB são perpendiculares.
Então, OACB é um quadrado e
OA = OB = BC = AC = 1m

29. B 1 C S
θ
1
T
θ
O A
1
Como OACB é um quadrado , então BC e OA são
paralelas.
Sendo AS tansversal a essas duas retas paralelas,
então o ângulo OSC também mede θ
ˆ

30. y
B 1 C S
θ
1 z
T
θ x
O A
1
Pelo triângulo OAT, temos :
x
tg θ = ⇒ x = tgθ
1
Pelo triângulo OSB, temos :
1 1
tg θ = ⇒ y = ⇒ y = cotgθ
y tg θ

31. y
B 1 C S
θ
1 z
T
θ x
O 1 A
Se y = cotg θ , então CS = cotg θ − 1
cos θ cos θ − senθ
−1
cotg θ − 1
cos θ = ⇒ z = sen θ = senθ
z cos θ cos θ
cos θ − senθ 1 cos θ − senθ
z= ⋅ =
senθ cos θ senθ cos θ
cos θ senθ 1 1
z= − = −
senθ cos θ senθ cos θ senθ cos θ

32. y
B 1 C S
θ
1 z
T
θ x
O 1 A
1 1
z= − = cossecθ − sec θ
senθ cos θ
Já sabemos que :
OA = OB = 1 e também que y = cotg θ e x = tgθ
Então o prímetro do polígono AOBSTA, em função de θ é :
2 + cotgθ + tgθ + cossecθ − secθ

33. 37) (UNIRIO) O valor numérico da expressão:
π
sen + cos 240º −[ tg ( − 750º ) ]
2
4 é:
 9π   5π 
( sec1200º )  cos sec  +  cotg 
 4   6 
(
a) 3 + 2 / 6 )
(
b) − 3 + 2 / 6 )
(
c) 3 − 2 / 6 )
(
d) − 3− 2 / 6 )
e)0

34. Solução
π 2
sen = sen 45º =
4 2
1
cos 240º = − cos 60º = −
2
3
tg ( - 750 ) = tg 330º = tg 30º =
3
1 1 1
sec1200º = = =− = −2
cos 1200º cos 120º cos 60º

35. 9π  9.180  1
cossec = cossec  = cossec 405º = =
4  4  sen 405º
1 2 2 2
= = = = 2
sen 45º 2 2
5π  5.180 
cotg = cotg  = cotg 150º = − cotg 30º =
6  6 
3 3 3
=− =− =− 3
3 3

36. π
sen + cos 240º −[ tg ( − 750º ) ]
2
4 =
 9π   5π 
( sec1200º )  cos sec  +  cotg 
 4   6 
2
2 1  3 2 1 3 3 2 −3− 2
− − 
− −
2 2  3 
  = 2 2 9= 6
= =
(
− 2. 2 + − 3
2
)
−2 2 +3 −2 2 +3
3 2 −5 1 3 2 −5
= ⋅ =
6 − 2 2 + 3 − 12 2 + 18

37. 3 2 −5 (
- 12 2 − 18)=
(
− 12 2 + 18 - 12 2 − 18)
− 72 − 54 2 + 60 2 + 90
=
288 − 324
18 + 6 2
=−
(
3+ 2 ) letra b
− 36 6

38. 99π  16π 
38) O valor de cos + tg  −  é:
4  3 
a) ( 3 − 2)/ 2
b)(3 2 + 2 3 ) / 6
c ) − (3 2 + 2 3 ) / 6
d) − ( 3 + 2) / 2
e) − ( 3 + ( 2 / 2 ) )

39. Solução
99π 99 ⋅180
Transformando em graus, temos : = 4455º
4 4
Calculando a MDP de 4455, temos :
4455 360
135 12
 99π 
Logo, cos  = cos 4455º = cos 135º =
 4 
2
= − cos 45º = −
2

40. 16π 16 ⋅180
Transformando em graus, temos : = 960º
3 3
16π
Calculando a MDP de , temos :
3
960 360
240 2
 16π 
Logo, tg −  = tg ( − 960º ) = tg ( − 240º )
 3 
= tg120º = −tg 60º = − 3

41.  99π   16π 
cos  + tg − =
 4   3 
2 − 2 −2 3
=− − 3= =
2 2
 2 
= −
 2 + 3

  letra e