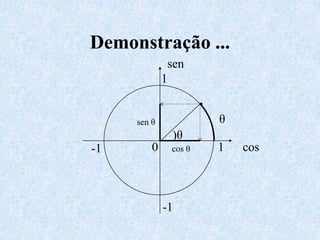
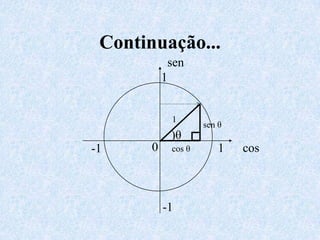
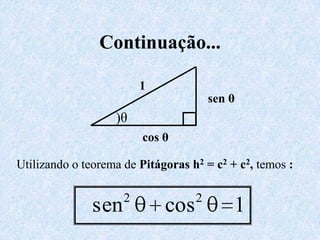
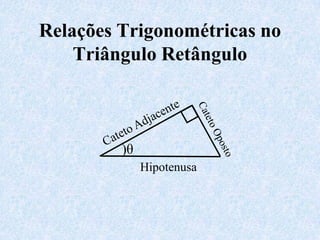
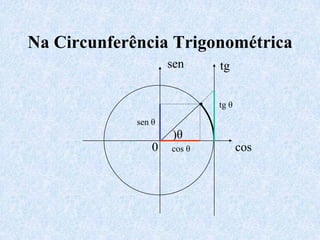
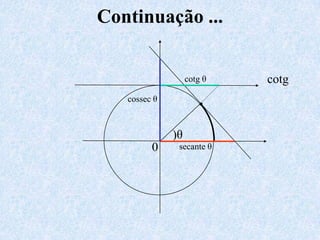
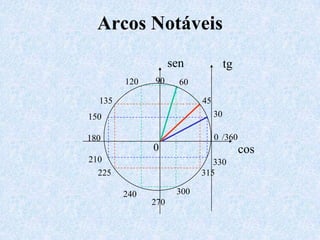
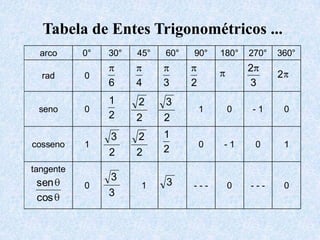
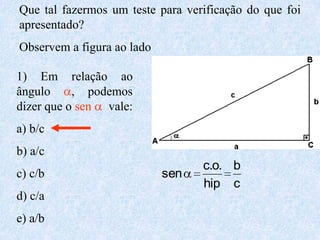
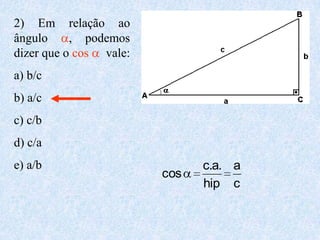
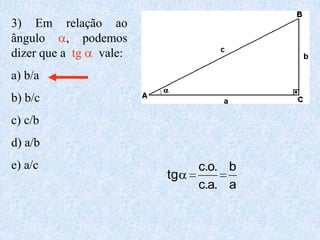
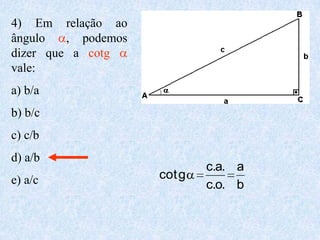
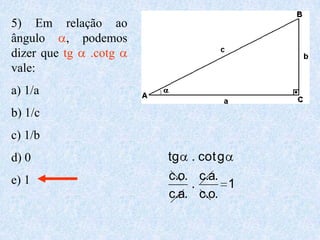
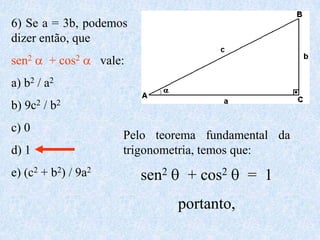
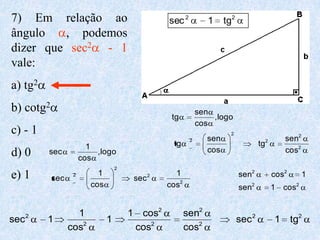
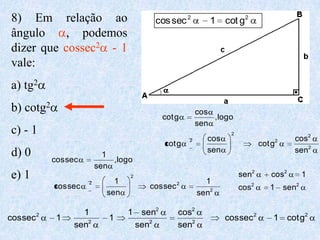
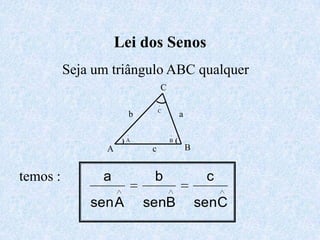
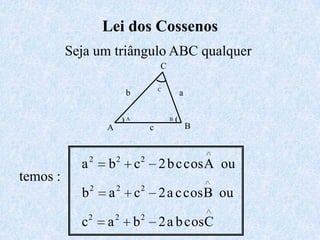
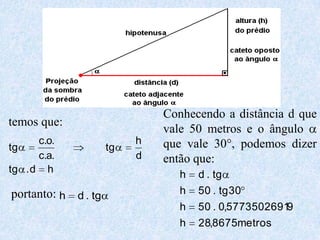
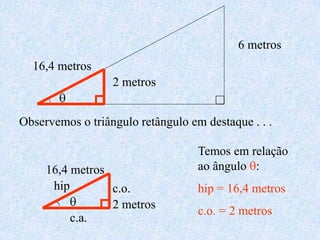
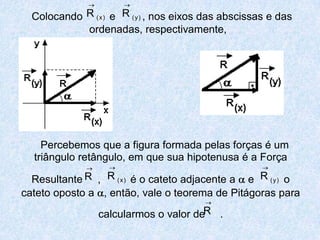
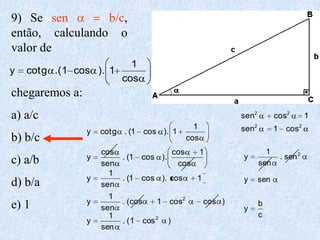
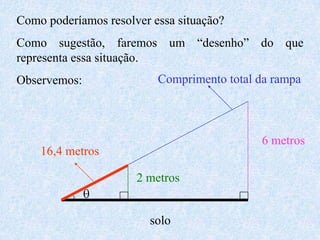
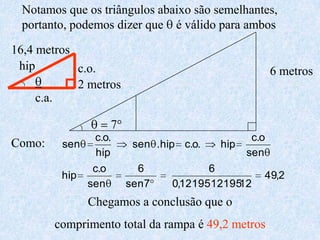
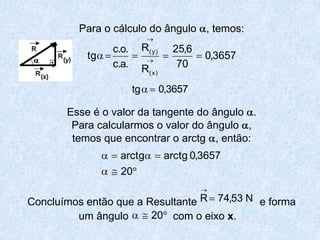
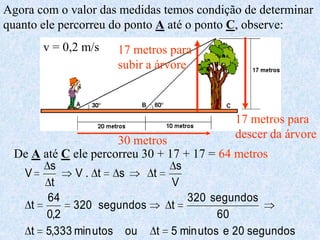
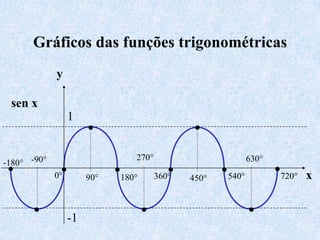
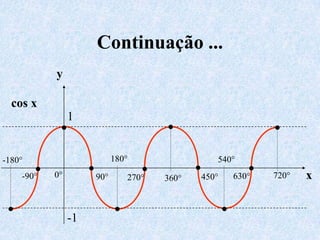
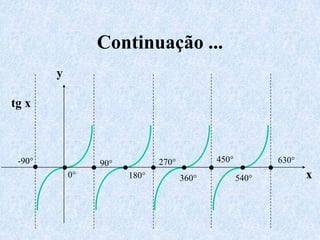
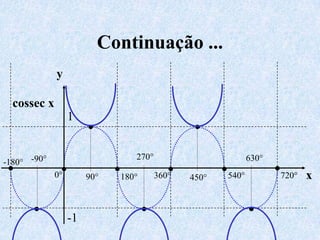
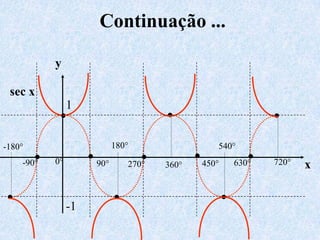
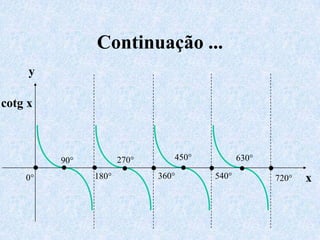
1) O documento apresenta as definições e propriedades fundamentais da trigonometria, incluindo o Teorema Fundamental da Trigonometria, as relações trigonométricas no triângulo retângulo e as leis dos senos e cossenos. 2) Inclui demonstrações das fórmulas trigonométricas e exemplos numéricos de cálculos envolvendo seno, cosseno e tangente. 3) Discutem transformações trigonométricas e como calcular valores de funções trigonométricas para ângulos não

1. Teorema Fundamental da
Trigonometria
2 2
sen cos 1

2. Demonstração ...
sen
1
·
sen θ θ
)θ
-1 0 cos θ 1 cos
-1

3. Continuação...
sen
1
1
sen θ
)θ
-1 0 cos θ 1 cos
-1

4. Continuação...
1
sen θ
)θ
cos θ
Utilizando o teorema de Pitágoras h2 = c2 + c2, temos :
2 2
sen cos 1

5. Relações Trigonométricas no
Triângulo Retângulo
)θ
Hipotenusa

6. Continuação ...
Ente Trigonométrico Relação no Triângulo Retângulo
CO
Seno de θ sen
HI
Cosseno de θ CA
cos
HI
Tangente de θ CO
tg
CA
1 HI
Cossecante de θ cos sec
sen CO
1 HI
Secante de θ sec
cos CA
Cotangente de θ 1 CA
cot g
tg CO

7. Na Circunferência Trigonométrica
sen tg
· tg θ
sen θ
)θ
0 cos θ cos

8. Continuação ...
cotg θ cotg
cossec θ
·
)θ
0 secante θ

9. Arcos Notáveis
sen tg
120 90 60
135 45
150 30
180 0 /360
0 cos
210 330
225 315
240 300
270

10. Tabela de Entes Trigonométricos ...
arco 0° 30° 45° 60° 90° 180° 270° 360°
2
rad 0 2
6 4 3 2 3
1 2 3
seno 0 1 0 -1 0
2 2 2
3 2 1
cosseno 1 0 -1 0 1
2 2 2
tangente
3 3
sen 0 1 --- 0 --- 0
cos 3

11. Transformações trigonométricas

12. Como podemos calcular o seno,
cosseno e a tangente de ângulos
não notáveis mais que podem ser
encontrados a partir de outros
dois notáveis?

13. Exemplos:
a)sen 15º
b) cos 75º
c) sem 105º
d) tg 75º

14. Será que:
sen(a + b) = sen a + sen b ?
sen(a - b) = sen a - sen b ?
cos(a + b) = cos a + cos b ?
cos (a - b) = cos a - cos b ?
tg(a + b) = tg a +tgb ?
tg (a - b) = tg a - tg b ?

15. Fórmulas da adição e subtração

16. Vamos pensar . . .

17. Que tal fazermos um teste para verificação do que foi
apresentado?
Observem a figura ao lado
1) Em relação ao
ângulo , podemos
dizer que o sen vale:
a) b/c
b) a/c
c.o. b
c) c/b sen
hip c
d) c/a
e) a/b

18. 2) Em relação ao
ângulo , podemos
dizer que o cos vale:
a) b/c
b) a/c
c) c/b
d) c/a
e) a/b c.a. a
cos
hip c

19. 3) Em relação ao
ângulo , podemos
dizer que a tg vale:
a) b/a
b) b/c
c) c/b
d) a/b
e) a/c c.o. b
tg
c.a. a

20. 4) Em relação ao
ângulo , podemos
dizer que a cotg
vale:
a) b/a
b) b/c
c) c/b
d) a/b
c.a. a
e) a/c cot g
c.o. b

21. 5) Em relação ao
ângulo , podemos
dizer que tg .cotg
vale:
a) 1/a
b) 1/c
c) 1/b
d) 0 tg . cot g
e) 1 c.o. c.a.
. 1
c.a. c.o.

22. 6) Se a = 3b, podemos
dizer então, que
sen2 + cos2 vale:
a) b2 / a2
b) 9c2 / b2
c) 0
Pelo teorema fundamental da
d) 1 trigonometria, temos que:
e) (c2 + b2) / 9a2 sen2 + cos2 = 1
portanto,

23. 7) Em relação ao sec 2 1 tg2
ângulo , podemos
dizer que sec2 - 1
vale:
a) tg2
b) cotg2 sen
tg ,logo
cos
c) - 1 2
2 sen 2 sen2
1 tg tg
d) 0 sec ,log o cos cos2
cos
2
e) 1 2 1 2 1 sen2 cos2 1
sec sec
cos cos2 sen2 1 cos2
2 1 1 cos2 sen2
sec 1 1 sec 2 1 tg2
cos2 cos2 cos2

24. 8) Em relação ao cos sec 2 1 cot g2
ângulo , podemos
dizer que cossec2 - 1
vale:
a) tg2
b) cotg2 cos
cot g , log o
sen
c) - 1 2
2 cos 2 cos2
cot g cot g
d) 0 sen sen2
1
cos sec ,log o
sen
e) 1 2 1
2
1
sen2 cos2 1
cos sec cos sec 2 cos2 1 sen2
sen sen2
2 1 1 sen2 cos2
cos sec 1 1 cos sec 2 1 cot g2
sen2 sen2 sen2

25. 9) Se sen b/c,
então, calculando o
valor de
1
y cot g .( 1 cos ). 1
cos
chegaremos a:
a) a/c sen2 cos2 1
1 sen2 1 cos2
y cot g . (1 cos ). 1
b) b/c cos
cos cos 1 1
y . (1 cos ). y . sen 2
c) a/b sen cos sen
1
y . (1 cos ). cos 1 y sen
d) b/a sen
1
y . (cos 1 cos2 cos )
e) 1 sen y
b
1 c
y . (1 cos 2 )
sen

26. Voltando
a parte teórica

27. Lei dos Senos
Seja um triângulo ABC qualquer
C
^
C
b a
^ ^
)A B (
A c B
temos : a b c
sen A senB senC

28. Lei dos Cossenos
Seja um triângulo ABC qualquer
C
^
C
b a
^ ^
)A B (
A c B
a2 b 2 c 2 2 b c cos A ou
temos :
b2 a 2 c 2 2 a c cos B ou
2 2 2
c a b 2 a b cosC

29. Continuação ...
Curiosidade : Quando um dos ângulos do triângulo é
reto, por exemplo, Â= 90°, temos :
2 2 2
a b c 2 b c cos 90
Sabe-se que cos 90° = 0, logo ...
2 2 2
a b c 2bc0
Temos, portanto ... 2 2 2
a b c Teorema de Pitágoras

30. Gráficos das funções trigonométricas
y
sen x
1
• •
270° 630°
-180° -90°
• •
0° 90°
•180° •
360° 450°
•540° •720° x
• -1 • •

31. Continuação ...
y
cos x
1
• • •
-180° 180° 540°
•
-90° 0° • 90° •
270° 360°
•450° •
630° 720° x
• -1
• •

32. Continuação ...
y
tg x
450° 630°
• •0° • •180° • • • • •
-90° 90° 270°
360° 540° x

33. Continuação ...
y
cossec x
1
• •
270° 630°
-180° -90°
• •
0° 90°
•180° •
360° 450°
•540° •720° x
• -1
• •

34. Continuação ...
y
sec x
1
• • •
-180° 180° 540°
-90°• 0° • 90° •
270° 360°
• 450° •
630° 720° x
• -1
• •

35. Continuação ...
y
cotg x
90° 270° 450° 630°
0°
• • •180° • • 360° • •540° • • 720° x

36. TRIGONOMETRIA APLICADA
• Modelo matemático que indica ao número de horas do dia,
com luz solar, de uma determinada cidade norte americana,
“t” dias após 1º de janeiro.
2
L( t ) 12 2,8 sen ( t 80 )
365
Fonte : J.Stewart – Cálculo vol. I – Pág. 34

37. Trigonometria
Algumas Aplicações

38. Parte Prática
O exemplo clássico da Sombra
Para que possamos medir (aproximadamente)
a altura de um prédio, sem a necessidade de subir
ao terraço, ou utilizar equipamentos sofisticados,
seria necessário somente 2 elementos.
São eles: uma distância
um ângulo
Observe a seguir . . .

39. Conhecendo a distância d que
temos que:
vale 50 metros e o ângulo
c.o. h que vale 30°, podemos dizer
tg tg
c.a. d então que:
tg . d h
h d . tg
portanto: h d . tg h 50 . tg 30
h 50 . 0,57735026919
h 28,8675metros

40. Exemplo 1
A inclinação de uma rampa

41. Uma rampa com inclinação constante, (como
a que existe em Brasília) tem 6 metros de
altura na sua parte mais elevada. Um
engenheiro começou a subir, e nota que após
ter caminhado 16,4 metros sobre a rampa está
a 2,0 metros de altura em relação ao solo. Será
que este engenheiro somente com esses dados
e uma calculadora científica conseguiria
determinar o comprimento total dessa rampa e
sua inclinação em relação ao solo?

42. Como poderíamos resolver essa situação?
Como sugestão, faremos um “desenho” do que
representa essa situação.
Observemos: Comprimento total da rampa
6 metros
16,4 metros
2 metros
solo

43. 6 metros
16,4 metros
2 metros
Observemos o triângulo retângulo em destaque . . .
Temos em relação
16,4 metros ao ângulo
hip c.o. hip = 16,4 metros
2 metros
c.o. = 2 metros
c.a.

44. Como: 16,4 metros
hip = 16,4 metros hip c.o.
2 metros
c.o. = 2 metros c.a.
c.o. 2
sen 0,1219512195 12
hip 16,4
Obs.: quando dizemos que arcsen = 1/2 , podemos
transformar essa igualdade em uma pergunta: “qual é o arco,
cujo seno vale 1/2?”, a resposta seria dizer que = 30°.

45. Em nosso exercício, chegamos a conclusão que:
sen = 0,121951219512, logo podemos encontrar o
ângulo , com o auxílio da calculadora que
normalmente utiliza as funções ASIN ou SIN-1, então,
devemos digitar 0,121951219512 e a opção acima de
sua calculadora.
Se o processo foi realizado corretamente, deverá
ser encontrado o valor 7,00472640907, que iremos
considerar como aproximadamente 7°.
Encontramos assim, a inclinação da rampa!

46. Notamos que os triângulos abaixo são semelhantes,
portanto, podemos dizer que é válido para ambos
16,4 metros
hip c.o. 6 metros
2 metros
c.a.
c.o. c.o
Como: sen sen . hip c.o. hip
hip sen
c.o 6 6
hip 49,2
sen sen 7 0,121951219512
Chegamos a conclusão que o
comprimento total da rampa é 49,2 metros

47. Exemplo 2
Mecânica Geral
ou Trigonometria?

48. Os conceitos trigonométricos aparecem com muita freqüência
no estudo da Física, Topografia, Astronomia e de muitos outros
assuntos.
Observemos os exemplos a seguir:
Em relação ao sistema de forças representado na figura, onde
F1 = 20N, F2 = 100N, F3 = 40N e F4 = 10N, você seria capaz de
determinar a intensidade da resultante do sistema e o ângulo
que essa resultante forma com o eixo das abscissas (x)?

49. Em primeiro lugar, teremos que fazer as projeções de F 2 nos eixos das abscissas e das
ordenadas, obtendo assim, respectivamente os componentes F 2 ( x ) eF 2 ( y ) .
Analogamente, encontraremos as projeções de F 3 , encontrando os componentesF 3 ( x ) eF 3 ( y ) .

50. R (x)
A resultante relativa ao eixo das abscissas é obtida
da seguinte maneira:
R ( x ) F 2 ( x ) F1 F 3 ( x )
c.a F2 ( x )
cos . cos 45 cos 45 .F2 F2 ( x ) F2 ( x ) F2 . cos 45
hip F2
Como
c.a F3 ( x )
cos . cos 60 cos 60 .F3 F3 ( x ) F3 ( x ) F3 . cos 60
hip F3
F2 ( x ) F2 . cos 45 100. 0,70 F2 ( x ) 70N
Por tan to
F3 ( x ) F3 . cos 60 40. 0,5 F3 ( x ) 20N
R ( x) F 2( x) F1 F 3 ( x)
R ( x ) 70 20 20
R ( x ) 70 N

51. R (y)
A resultante relativa ao eixo das abscissas é obtida
da seguinte maneira:
R (y) F 2(y) F 4 F 3(y)
c.o F2 ( y )
sen . sen 45 sen 45 .F2 F2 ( y ) F2 ( y ) F2 . sen 45
hip F2
Como
c.o F3 ( y )
sen . sen 60 sen 60 .F3 F3 ( y ) F3 ( y ) F3 . sen 60
hip F3
F2 ( y ) F2 . sen 45 100. 0,70 F2 ( y ) 70N
Por tan to
F3 ( y ) F3 . sen 60 40. 0,86 F2 ( y ) 34,4 N
R (y) F 2(y) F 4 F 3(y)
R ( y ) 70 10 34,4
R ( y ) 25,6 N

52. Colocando R ( x ) e R ( y ) , nos eixos das abscissas e das
ordenadas, respectivamente,
Percebemos que a figura formada pelas forças é um
triângulo retângulo, em que sua hipotenusa é a Força
Resultante R , R ( x ) é o cateto adjacente a e R ( y ) o
cateto oposto a , então, vale o teorema de Pitágoras para
calcularmos o valor deR .

53. h2 c 2 c 2
2 2 2
R R (x) R (y)
2
2 2
R 70 25,6
2
R 4900 655,36
2
R 5555,36
R 5555,36
R 74,53 N

54. Para o cálculo do ângulo , temos:
c.o. R( y ) 25,6
tg 0,3657
c.a. R( x ) 70
tg 0,3657
Esse é o valor da tangente do ângulo
Para calcularmos o valor do ângulo ,
temos que encontrar o arctg , então:
arctg arctg 0,3657
20
Concluímos então que a Resultante R 74,53 N e forma
um ângulo 20 com o eixo x.

56. Um alpinista muito ágil, percorre um trajeto passando pelos
pontos A e B. Não se sabe ao certo o que ocorreu, mas ele
conseguiu com o material apropriado chegar a conclusão das
medidas abaixo mencionadas. Quando chega até a árvore ele
percebe que o único caminho que o levará até o ponto C é
escalando-a. (a altura da árvore é representada por h - despreze a
largura do tronco)
Se sua velocidade média é de 0,2 m/s, quantos minutos ele
demorou para sair do ponto A e chegar ao ponto C? ( 3 1,7 )

57. Solução:
Resumidamente, temos o
triângulo ao lado que
representa nosso desafio.
c.o. h
tg 30 tg 30 . (20 y ) h h tg 30 . (20 y )
c.a. (20 y )
3
h . (20 y ) ( I )
3
c.o. h
tg 60 tg 60 . y h h tg 60 . y
c.a. y
h 3 . y ( II )

58. Igualando o h das equações ( I ) e (II)
3
(I) h . (20 y ) ( II ) h 3 .y
3
3
. (20 y ) 3 .y 3 . (20 y ) 3. 3 .y
3
(20 y ) 3 . y 20 3y y 20 2y
y 10 metros
Como
h 3 .y
h 17 .10
,
h 17 metros

59. Agora com o valor das medidas temos condição de determinar
quanto ele percorreu do ponto A até o ponto C, observe:
v = 0,2 m/s 17 metros para
subir a árvore
17 metros para
descer da árvore
30 metros
De A até C ele percorreu 30 + 17 + 17 = 64 metros
s s
V V. t s t
t V
64 320 segundos
t 320 segundos t
0,2 60
t 5,333 min utos ou t 5 min utos e 20 segundos

60. Obrigado pela
participação de todos!!!
Prof. Luciano
Ribeiro